FORÇA ELÉTRICA – LEI DE COULOMB

Lei de Coulomb

 Na figura abaixo você observa o esquema de uma balança de torção parecido com a que Coulomb utilizou para medir forças elétricas de atração ou de repulsão entre partículas eletrizadas. Partículas eletrizadas podem ser denominadas também de cargas elétricas pontuais ou puntiformes (corpos de dimensões muito pequenas cuja carga está localizada em um único ponto).

Essa balança é constituída por uma haste (h) de material isolante com uma esfera metálica eletrizada com carga q numa ponta e na outra ponta, um contrapeso (cp) para manter a haste na horizontal. Esta haste está suspensa por uma fibra fina isolante presa a um ponteiro com uma escala graduada.

Coulomb colocou próximo de q uma esfera eletrizada com carga Q e, sendo q e Q positivas, surgiu força de repulsão entre elas, fazendo com que a fibra girasse de certo ângulo α₁, indicado na escala graduada.

Repetindo esta experiência e variando a distância entre as cargas eletrizadas, Coulomb percebeu que a força elétrica era inversamente proporcional ao quadrado da distância e diretamente proporcional à quantidade de carga elétrica de cada partícula, ou seja, F =Q.q/d².

Para se transformar essa proporção em igualdade é preciso uma constante de proporcionalidade (K) e, a lei de Coulomb, matematicamente fica:

A expressão matemática acima é denominada lei de Coulomb e de enunciado:

Esta constante K é dependente do meio onde estão as cargas (denominada constante eletrostática do meio ou constante dielétrica) e, no sistema internacional de unidades (SI) e, no vácuo e aproximadamente no ar, tem valor K = 1/4πε_o ≈ 8,9876.10⁹ Nm²/C² costuma ser arredondado para K = 9.10⁹ Nm²/C².

 Essa força de interação é um vetor que tem a mesma intensidade agindo sobre cada carga,

mesma direção (da reta que une cada carga) e sentidos opostos e, consequentemente são par ação e reação.

O que você deve saber, informações e dicas

Lei de Coulomb

Essa força de interação é um vetor que tem a mesma intensidade agindo sobre cada carga,

mesma direção (da reta que une cada carga) e sentidos opostos e, consequentemente são par ação e reação.

Determinando a intensidade, direção e sentido da força elétrica resultante sobre uma carga devido à ação de outras cargas.

Exercícios de vestibulares com resolução comentada sobre

FORÇA ELÉTRICA – LEI DE COULOMB

01- (UNIFESP-SP) Duas partículas de cargas elétricas

Q₁ = 4,0 × 10^-16 C e q‚ = 6,0 × 10^-16 C

estão separadas no vácuo por uma distância de 3,0.10^-9m. Sendo k = 9,0.10⁹ N.m²/C², a intensidade da força de interação entre elas, em newtons, é de

02-(UEL-PR) Duas cargas iguais de 2.10^-6C, se repelem no vácuo com uma força de 0,1N. Sabendo-se que a constante elétrica do vácuo é 9.10⁹Nm²/C², a distância entre as cargas, em metros, é de:

03-(UNESP-SP) Qual dos gráficos representa a maneira como varia a força elétrica entre duas cargas pontuais em função da distância que as separa, quando são aproximadas ou afastadas uma da outra?

04-(MACKENZIE-SP) Dois corpúsculos eletrizados com cargas elétricas idênticas estão situados no vácuo (K_o=9.0.10⁹N.m²/C²) e

distantes 1m um do outro. A intensidade da força de interação eletrostática entre eles é 3,6.10^-2 N. A carga elétrica de cada um desses corpúsculos pode ser (em μC):

05-(PUC-MG) Duas cargas elétricas puntiformes são separadas por uma distância de 4,0 cm e se repelem mutuamente com uma força de 3,6 × 10^-5 N. Se a distância entre as cargas for aumentada para 12,0 cm, a força entre as cargas passará a ser de:

06-(UNESP-SP) Dois corpos pontuais em repouso, separados por certa distância e carregados eletricamente com cargas de sinais iguais, repelem-se de acordo com a Lei de Coulomb.

a) Se a quantidade de carga de um dos corpos for triplicada, a força de repulsão elétrica permanecerá constante, aumentará (quantas vezes?) ou diminuirá (quantas vezes?)?

b) Se forem mantidas as cargas iniciais, mas a distância entre os corpos for duplicada, a força de repulsão elétrica permanecerá constante, aumentará (quantas vezes?) ou diminuirá (quantas vezes?)?

07-(UFRN-RN) Se q₁ e q₂ forem duas cargas elétricas, para a situação esquematizada necessariamente ter-se-á:

08-(UEPG-PR) A interação eletrostática entre duas cargas elétricas q₁ e q₂, separadas uma da outra por uma distância r, é F₁. A carga q₂ é removida e, a uma distância 2r da carga q₁, é colocada uma carga q₃ cuja intensidade é a terça parte de q₂. Nesta nova configuração, a interação eletrostática entre q₁ e q₃ é – F₂. Com base nestes dados, assinale o que for correto.

(01) As cargas q1 e q₂ têm sinais opostos.

(02) As cargas q₂ e q₃ têm sinais opostos.

(04) As cargas q₁ e q₃ têm o mesmo sinal.

(08) A força F₂ é repulsiva e a força F₁ é atrativa.

(16) A intensidade de F₂ = F₁/12

09- (UERJ-RJ) Seja f a força de repulsão entre duas partículas de mesma carga q, separadas por uma distância r. Assim , qual das duas figuras abaixo melhor ilustra as forças de repulsão entre duas partículas de cargas 2q e 3q, separadas pela mesma distância r ?

10-(PUC-RJ) Duas esferas carregadas, afastadas de 1 m, se atraem com uma força de 720 N. Se uma esfera tem o dobro da carga da segunda, qual é a carga das duas esferas?

(Considere k = 9 . 10⁹ Nm²/C²)

11-(FGV-SP) Sendo k a constante eletrostática e G a constante de gravitação universal, um sistema de dois corpos idênticos, de

mesma massa M e cargas de mesma intensidade +Q, estarão sujeitos a uma força resultante nula quando a relação M/Q for igual a

12-(FUVEST-SP) A uma distância d uma da outra, enc=ontram-se duas esferinhas metálicas idênticas, de dimensões desprezíveis, com cargas -Q e +9Q. Elas são postas em contacto e, em seguida, colocadas à distância 2d. A razão entre os módulos das forças que

atuam após o contacto e antes do contacto é

13-(UFPE) O gráfico a seguir representa a força F entre duas cargas puntiformes positivas de

mesmo valor, separadas pela distância r. Considere K=9.10⁹ N.m²C² e determine o valor das cargas, em unidades de 10^-7C.

14-(UFRGS) Deposita-se, uniformemente, carga elétrica no valor de +5.10-5 C sobre uma pequena esfera não condutora. Uma partícula com carga -3.10^-6 C, colocada a 30 cm da esfera, sofre uma força atrativa de módulo 15 N. Outra partícula, com carga

-6.10^-6 C, colocada a 60 cm da esfera, sofrerá uma força atrativa de módulo, em N:

15-(FATEC-SP) Duas pequenas esferas estão, inicialmente, neutras eletricamente. De uma das

esferas são retirados 5,0 × 10¹⁴elétrons que são transferidos para a outra esfera. Após essa operação, as duas esferas são afastadas de 8,0 cm, no vácuo

Dados: carga elementar e = 1,6 × 10^-19C  ---  constante eletrostática no vácuo k_o = 9,0 × 10⁹N.m²/C²

A força de interação elétrica entre as esferas será de

a) atração e intensidade 7,2 ×10⁵N.               

b) atração e intensidade 9,0 × 10³N.              

c) atração e intensidade 6,4 × 10³N.

d) repulsão e intensidade 7,2 × 10³N.            

e) repulsão e intensidade 9,0 × 10³N.

16-(UFGO) Em quatro vértices de um pentágono regular são colocadas cargas de mesmo valor Q,

mas de sinais alternados,conforme  a figura.  No 5º e último vértice do pentágono é colocada uma carga de prova q0 > 0, que ficará sob a ação de todas as outras. Qual dos vetores , , , ou representa a resultante das ações das cargas + Q e – Q sobre q_o?

17- (UNESP-SP) Considere uma experiência em que três cargas pontuais de igual módulo estejam alinhadas e igualmente espaçadas, que as cargas A e C sejam fixas, e que os sinais das cargas A, B e C obedeçam a uma das três configurações seguintes:

 Considere, ainda, que se deseja que a carga B esteja solta e em equilíbrio.  Para tanto, das configurações apresentadas, pode-se usar

a) somente a 1.              

b)somente a 2.            

c) somente a 3.               

d)tanto a 1 quanto a 3.           

e)tanto a 1 quanto a 2.

18-(PUCCAMP-SP) Nos pontos de abscissa x=2 e x=5 são fixadas as cargas Q e 4Q, respectivamente, conforme mostra o esquema a

seguir: Uma terceira carga –Q, ficará em equilíbrio, sob ação somente das forças elétricas exercidas por Q e 4Q, quando colocada no ponto de abscissa igual a:

19-(UFC-CE) Uma partícula com carga positiva +q é fixada em um ponto, atraindo uma outra partícula com carga negativa -q e massa m, que se move em uma trajetória circular de raio R, em torno da carga positiva, com velocidade de módulo constante (veja a figura a seguir). Considere que não há qualquer forma de dissipação de energia, de modo que a conservação da energia mecânica é observada no sistema de cargas. Despreze qualquer efeito da gravidade. A constante eletrostática é igual a k.

a) Determine o módulo da velocidade v com que a carga negativa se move em torno da carga positiva.

b) Determine o período do movimento circular da carga negativa em torno da carga positiva.

20-(UNESP-SP) Três pequenas esferas estão carregadas eletricamente com cargas q₁, q₂ e q₃ e alinhadas sobre um plano horizontal sem atrito (no vácuo), conforme a figura.

Nessa situação elas se encontram em equilíbrio. A carga da esfera q₂ é positiva e vale 2,7.10^-4C.

Pede-se:

a) Determinar os sinais das cargas q₁ e q_3. Justificar.

b) Calcular os valores das cargas q₁ e q₃.

c) Se forem fixada as posições de q₁ e de q₃, qual será o tipo de equilíbrio (estável, instável ou indiferente) da esfera de carga q₂?

21-(UFRS-RS) Três cargas elétricas puntiformes idênticas, Q₁, Q₂ e Q₃, são mantidas fixas em suas posições sobre uma linha reta,

conforme indica a figura a seguir. Sabendo-se que o módulo da força elétrica exercida por Q₁sobre Q₂ é de 4,0.10^-5 N, qual é o módulo da força elétrica resultante sobre Q₂?

22-(UFRS-RS) A figura a seguir representa duas cargas elétricas puntiformes positivas, +q e +4q,

mantidas fixas em suas posições.Para que seja nula a força eletrostática resultante sobre uma terceira carga puntiforme, esta carga deve ser colocada no ponto

23-(UFMG-MG) Duas pequenas esferas isolantes - I e II -, eletricamente carregadas com cargas de sinais contrários, estão fixas nas posições representadas nesta figura:

A carga da esfera I é positiva e seu módulo é maior que o da esfera II.

Guilherme posiciona uma carga pontual positiva, de peso desprezível, ao longo da linha que une essas duas esferas, de forma que ela fique em equilíbrio.

Considerando-se essas informações, é CORRETO afirmar que o ponto que melhor representa a posição de equilíbrio da carga pontual, na situação descrita, é o

 24-(FUVEST-SP) Três objetos com cargas elétricas idênticas estão alinhados como mostra a figura. O objeto C exerce sobre B uma força igual a 3,0.10^-6 N. A força elétrica resultante dos efeitos de A e C sobre B é:

a) 2,0.10^-6 N.                       

b) 6,0.10^-6 N.                          

c) 12.10^-6 N.                   

d) 24.10^-6 N.                     

e) 30.10^-6 N.

25-(FUVESP-SP) Duas barras isolantes, A e B, iguais, colocadas sobre uma mesa, têm em suas extremidades, esferas com cargas elétricas de módulos iguais e sinais opostos. A barra A é fixa, mas a barra B pode girar livremente em torno de seu centro O, que permanece fixo. Nas situações I e II, a barra B foi colocada em equilíbrio, em posições opostas. Para cada uma dessas duas situações, o equilíbrio da barra B pode ser considerado como sendo, respectivamente,

a) indiferente e instável.     

b) instável e instável.     

c) estável e indiferente.    

d) estável e estável.            

e) estável e instável.

26-(PUC-RJ) Antes da primeira viagem à Lua, vários cientistas da NASA estavam preocupados com a possibilidade de a nave lunar se deparar com uma nuvem de poeira carregada sobre a superfície da Lua.

Suponha que a Lua tenha uma carga negativa. Então ela exerceria uma força repulsiva sobre as partículas de poeira carregadas também negativamente. Por outro lado, a força gravitacional da Lua exerceria uma força atrativa sobre estas partículas de poeira.

Suponha que a 2 km da superfície da Lua a atração gravitacional equilibre exatamente a repulsão elétrica, de tal forma que as partículas de poeira flutuem. 
Se a mesma nuvem de poeira estivesse a 5 km da superfície da Lua:

a) a gravidade ainda equilibraria a força eletrostática, mas apenas se a poeira perdesse carga.
b) a gravidade ainda equilibraria a força eletrostática, e as partículas de poeira também flutuariam.
c) a gravidade ainda equilibraria a força eletrostática, mas apenas se a poeira perdesse massa.
d) a gravidade seria maior que a força eletrostática, e a poeira cairia.
e) a gravidade seria menor que a força eletrostática, e a poeira se perderia no espaço.

27-(UFMG-MG) Observe a figura que representa um triângulo eqüilátero. Nesse triângulo, três cargas elétricas pontuais de mesmo valor absoluto estão nos seus vértices. O vetor que melhor representa a força elétrica resultante sobre a carga do vértice 1 é

28-(UFMG-MG) Na figura estão representadas três partículas com cargas idênticas tais

que│q₁│tais que│q₁│=│q₂│=│q₃│= 1μC,ocupando os vértices de um triângulo equilátero ABC de 3m de lado. Determine a intensidade, direção e sentido da força resultante elétrica que atua sobre a carga situada no vértice A. Considere K=9.10⁹N.m²/C²

29-(UNIFESP-SP) Na figura, estão representadas duas pequenas esferas de mesma massa, m=0,048kg, eletrizadas com cargas de mesmo sinal, repelindo-se, no ar. Elas estão penduradas por fios isolantes muito leves, inextensíveis, de mesmo comprimento L=0,090m. Observa-se que, com o tempo, essas esferas se aproximam e os fios tendem a tornarem-se verticais.

a) O que causa a aproximação dessas esferas? Durante essa aproximação, os ângulos que os fios formam com a vertical são sempre iguais ou podem tornar-se diferentes um do outro?

b) Suponha que, na situação da figura, o ângulo α é tal que senα=0,60; cosα=0,80 e tgα=0,75 e as esferas têm cargas iguais. Qual é, nesse caso, a carga elétrica de cada esfera? (Admitir g=10m/s² e K=9,0.10⁹N.m²/C²).

30-(UFPE) Quatro cargas elétricas puntiformes, de intensidades Q e q, estão fixas nos vértices de um quadrado, conforme indicado na figura. Determine a razão Q/q para que a força sobre cada uma das cargas Q seja nula.

31-(UFRJ-RJ) Duas cargas, q e -q são mantidas fixas a uma distância d uma da outra. Uma terceira carga q_o é colocada no ponto médio entre as duas primeiras, como ilustra a figura A. Nessa situação, o módulo da força eletrostática resultante sobre a carga q_o vale F_A.

A carga q_o é então afastada dessa posição ao longo da mediatriz entre as duas outras até atingir o ponto P, onde é fixada, como ilustra a figura B. Agora, as três cargas estão nos vértices de um triângulo equilátero. Nessa situação, o módulo da força eletrostática resultante sobre a carga q_o vale F_B.

Calcule a razão F_A/F_B.

32-(PUC-RJ) Dois objetos metálicos esféricos idênticos, contendo cargas elétricas de 1 C e de 5 C, são colocados em contato e depois afastados a uma distância de 3 m. Considerando a Constante de Coulomb k = 9.10⁹ N m²/C², podemos dizer que a força que atua entre as cargas após o contato é:

a) atrativa e tem módulo 3.10⁹ N.          

b) atrativa e tem módulo 9.10⁹ N.            

c) repulsiva e tem módulo 3.10⁹ N. 

d) repulsiva e tem módulo 9.10⁹ N.         

e) zero. 

 33-(PUC-RJ) Duas esferas idênticas, carregadas com cargas Q = 30 μ C, estão suspensas a partir de um mesmo ponto por dois

fios isolantes de mesmo comprimento como mostra a figura.

Em equilíbrio, o ângulo θ, formado pelos dois fios isolantes com a vertical, é 45°. Sabendo que a massa de cada esfera é de 1 kg, que a Constante de Coulomb é k = 9.10⁹ N m²/C² e que a aceleração da gravidade é g = 10 m/s², determine a distância entre as duas esferas quando em equilíbrio.

Lembre-se de que μ = 10^-6.

 34-(UNICAMP-SP) O fato de os núcleos atômicos serem formados por prótons e nêutrons

suscita a questão da coesão nuclear, uma vez que os prótons, que têm carga positiva q = 1,6.10^-19 C , se repelem através da força eletrostática. Em 1935, H. Yukawa propôs uma teoria para a força nuclear forte, que age a curtas distâncias e mantém os núcleos coesos.

a) Considere que o módulo da força nuclear forte entre dois prótons F_N é igual a vinte vezes o módulo da força eletrostática entre eles F_E , ou seja, F_N = 20 F_E. O módulo da força eletrostática entre dois prótons separados por uma distância d é dado por F_E = K(q²/d²), onde K = 9,0.10⁹Nm²/C². Obtenha o módulo da força nuclear forte F_N entre os dois prótons, quando separados por uma distância = 1,6.10^-15 m, que é uma distância típica entre prótons no núcleo.

b) As forças nucleares são muito maiores que as forças que aceleram as partículas em grandes aceleradores como o LHC. Num

 primeiro estágio de acelerador, partículas carregadas deslocam-se sob a ação de um campo elétrico aplicado na direção do movimento. Sabendo que um campo elétrico de módulo

E = 2,0.10⁵ N/C age sobre um próton num acelerador, calcule a força eletrostática que atua no próton.

35-(UNIFESP-SP)  Considere a seguinte "unidade" de medida: a intensidade da força elétrica entre duas cargas q, quando separadas por uma distância d, é F. Suponha em seguida que uma carga q₁ = q seja colocada frente a duas outras cargas, q₂ = 3q e

q₃ = 4q, segundo a disposição mostrada na figura. A intensidade da força elétrica resultante sobre a carga q₁, devido às cargas q₂ e q₃, será

36-(FGV-SP) Posicionadas rigidamente sobre os vértices de um cubo de aresta 1 m, encontram-

se oito cargas elétricas positivas de mesmo módulo. Sendo k o valor da constante eletrostática do meio que envolve as cargas, a força resultante sobre uma nona carga elétrica também positiva e de módulo igual ao das oito primeiras, abandonada em repouso no centro do cubo, terá intensidade:

a) zero.                 

b) k.Q².                     

c) k.Q².                          

d) 4k.Q⁴.                        

e) 8k.Q². 

37- (PUC-RJ) Três cargas elétricas estão em equilíbrio ao longo de uma linha reta de modo que

 uma carga positiva (+Q) está no centro e duas cargas negativas (–q) e (–q) estão colocadas em lados opostos e à mesma distância (d) da carga Q. Se aproximamos as duas cargas negativas para d/2 de distância da carga positiva, para quanto temos que aumentar o valor de Q (o valor final será Q’), de modo que o equilíbrio de forças se mantenha?

a) Q’ = 1 Q                   

b) Q’ = 2 Q                    

c) Q’ = 4 Q                       

d) Q’ = Q / 2                     

e) Q’ = Q / 4 

38-(PUC-RJ)  O que acontece com a força entre duas cargas elétricas (+Q) e (–q) colocadas a uma distância (d) se mudarmos a carga (+ Q) por (+ 4Q), a carga (–q) por (+3q) e a distância (d) por (2d)?

a) Mantém seu módulo e passa a ser atrativa. 

b) Mantém seu módulo e passa a ser repulsiva. 

c) Tem seu módulo dobrado e passa a ser repulsiva. 

d) Tem seu módulo triplicado e passa a ser repulsiva. 

e) Tem seu módulo triplicado e passa a ser atrativa. 

39-(ITA-SP) 

Considere uma balança de braços desiguais, de comprimentos ℓ₁ e ℓ₂, conforme mostra a figura. No lado esquerdo encontra-se pendurada uma carga de magnitude Q e massa desprezível, situada a uma certa distância de outra carga, q. No lado direito encontra-se uma massa m sobre um prato de massa desprezível. Considerando as cargas como puntuais e desprezível a massa do prato da direita, o valor de q para equilibrar a massa m é dado por

40-(UFU-MG)

Duas cargas +q estão fixas sobre uma barra isolante e distam entre si uma distância 2d. Uma outra barra isolante é fixada perpendicularmente à primeira no ponto médio entre essas duas cargas. O sistema é colocado de modo que esta última haste fica apontada para cima. Uma terceira pequena esfera de massa m e carga +3q furada é atravessada pela haste vertical de maneira a poder deslizar sem atrito ao longo desta, como mostra a figura a seguir. A distância de equilíbrio da massa m ao longo do eixo vertical é z.

Com base nessas informações, o valor da massa m em questão pode ser escrito em função de d, z, g e k, onde g é a aceleração gravitacional e k a constante eletrostática.

A expressão para a massa m será dada por:

41-(MACKENZIE-SP)

Duas cargas elétricas puntiformes, quando separadas pela distância d, se repelem com uma

força de intensidade F. Afastando-se essas cargas, de forma a duplicar a distância entre elas, a intensidade da força de repulsão será igual a

42-(IME-RJ)

Uma carga positiva está presa a um espelho plano. O espelho aproxima-se, sem rotação, com velocidade constante paralela ao eixo x, de uma carga negativa, pendurada ao teto por um fio inextensível. No instante ilustrado na figura, a carga

negativa se move no sentido oposto ao da carga positiva, com a mesma velocidade escalar do espelho. Determine, para esse instante:

a) as componentes x e y do vetor velocidade da imagem da carga negativa refletida no espelho;

b) as acelerações tangencial e centrípeta da carga negativa;

Dados:

ângulo entre o eixo x e o espelho: α;

ângulo entre o eixo x e o segmento de reta formado pelas cargas: β;

módulo das cargas elétricas; Q;

diferença entre as coordenadas y das cargas: d;

comprimento do fio: L;

velocidade escalar do espelho: V;

massa da carga negativa: m;

constante elétrica do meio: k

43-Questões interdisciplinares:

A população mundial hoje gira em torno de 7 bilhões de pessoas e até meados do século XXI deverá atingir 10 bilhões. De acordo com os cenários escolhidos para a procura energética, o consumo da energia primária mundial poderá atingir duas a três vezes o consumo atual.

Em 1990, o consumo de energia primária por habitante e por ano era de 5,1 TEP nos países industrializados e apenas 10% nos países em vias de desenvolvimento.

1TEP (Tonelada Equivalente de Petróleo) é a unidade de medição de consumo de energia e equivale a 10x109 cal.

1BEP (Barril Equivalente de Petróleo), variação da TEP, equivalente a 1,45x10⁹ cal.

Ou ainda que:

Uma fonte de energia capaz de corresponder de forma substancial a esta procura é a energia nuclear, através da FISSÃO e da FUSÃO nuclear. Vejamos:

Esse fenômeno da repulsão elétrica constitui um dos Princípios da Eletrostática, cujo módulo da força pode ser determinado pela Lei de Coulomb F=k.|Q₁|. |Q₂|./d².                   .

O quanto esta força atua está relacionado à carga, ao meio e à distância entre os centros dos núcleos das partículas que estão interagindo. Caso os núcleos conseguissem se aproximar o suficiente, prevalecendo a interação forte, ocorreria o fenômeno da fusão nuclear.

O controle dessa fusão nuclear continua sendo objeto de pesquisa. Essa fusão é o processo no qual dois núcleos de átomos leves (por exemplo, o hidrogênio – cujo núcleo é constituído por 1 próton com carga elétrica elementar é 1,6.10^-19 C) se combinam, ou se fundem, constituindo um elemento mais pesado. Os núcleos, então, carregados positivamente, devem se aproximar suficientemente um do outro, ou seja, vencer a força de repulsão eletrostática entre eles. 

Para que as reações de fusão possam ser produzidas a uma taxa conveniente, são necessárias temperaturas altíssimas, da ordem de 100 milhões de  graus Celsius e a pressão faz com que os átomos de  hidrogênio sejam comprimidos.

Os centros de seus núcleos devem estar a 1.10^-15 metros um do outro para que ocorra a fusão. Nesse estágio, eles se transformam em plasma. Uma característica especial desse estado é que, nele, a matéria reage a influências elétricas e magnéticas.

Por modestas que sejam as esperanças de chegar à fusão, estima-se que ainda demorará 30 anos para termos um reator comercial e, por mais caras que sejam as pesquisas, as vantagens da fusão são sedutoras.

Segundo todos os cálculos, as futuras usinas de fusão nuclear poderão extrair de 1 metro cúbico de água uma quantidade de energia igual à de 2 mil barris de petróleo.

a) Segundo as expectativas, após a instalação de um reator comercial com capacidade diária de 100 metros cúbicos de água para a fusão nuclear, qual seria a sua produção, diária, correspondente a Barris Equivalentes de Petróleo? (admita que 1 barril [159L] de petróleo de composição média contenha 1,5x10⁶ kcal)

b) Determine o valor da força elétrica repulsiva entre dois núcleos de hidrogênio quando colocados no vácuo e separados à distância necessária para a ocorrência da fusão nuclear.

Resolução comentada dos exercícios de vestibulares sobre

Força elétrica – Lei de Coulomb

01- F=KQq/d²=9.10⁹.4.10^-16.6.10^-16/(3.10^-9)²  ---  F=9.24.10^-23/9.10^-18  --- F=24.10^-5 N  ---  R- D

02- F=KQq/d²  ---  10^-1=9.10⁹.2.10^-6.2.10^-6/d²  ---  10^-1=36.10^-3/d²  ---  d²=36.10^-2  ---  d=6.10^-1m  ---  R- B

03- R- E  ---  veja teoria

04- Q₁=Q₂=Q  ---  F=KQq/d²  ---  3,6.10^-2=9.10⁹.Q.Q/(1)²  ---  Q²=3,6.10^-2/9.10⁹=0,4.10^-11  ---  Q²=4.10^-12  ---  Q=2.10^-6C  ---  R- E

05- Observe na expressão F=KQq/d² que a intensidade da força F é inversamente proporcional ao quadrado da distância  ---  se a distância ficou 3 vezes maior, a força deverá ficar 3³=9 vezes menor  ---  3,6.10^-5/9  ---  F=0,4.10^-5N  ---  R-B

06- a) Observe na expressão F=KQq/d² que a intensidade da força F é diretamente proporcional ao módulo de cada carga  --- se você triplicar o valor de uma das cargas a força elétrica ficará 3 vezes maior.

b) Observe na expressão F=KQq/d² que a força F é inversamente proporcional ao quadrado da distância entre as cargas  ---  se você duplicar a distância, a força elétrica ficará 2²=4 vezes menor.

07- Observe que a força é de repulsão o que significa que as cargas têm mesmo sinal, ou seja, (+).(+)>0 e (-).(-)>0  ---  R- C

08- F₁=Kq₁.q₂/r²  ---  F₁>0 (q₁ e q₂ tem mesmo sinal)  ---  -F₂=K.q₁.q₃/(2r)²=(Kq₁.q₂/3)/4r²  ---  -F₂=Kq₁.q₂/12r²  ---  F₂<0 (q₁ e q₃tem sinais opostos)  ---  F₁/F₂= Kq₁.q₂/r² X 12r²/Kq₁q₂  ---  F₁/F₂=12  ---  R- (02 + 16)=18

09-

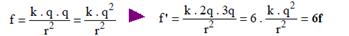
R- E

10- F=KQq/d²  ---  720=9.10⁹.Q.2Q/1²  ---  Q²=720/18.10⁹  ---  Q²=40.10^-9  ---  Q=√(4.10^-8)  ---  Q=2.10^-4C e Q’=4.10^-4C

11- Força elétrica  ---  F_e=KQq/d²  ---  força gravitacional  ---  F_G=GMm/d²  ---  igualando-as  ---  KQq/d² = GMm/d²  ---  KQ²/d² = GM²/d²  ---  M²Q²=KG  ---  MQ=√(KG)  ---  R- C

12- Antes do contato  ---  F_a=KQq/d²=KQ.9Q/d²  ---  F_a=9KQ²/d²  ---  após colocadas em contato e separadas cada uma fica com carga Q’ tal que Q’= (-Q + 9Q)/2  ---  Q’=  4Q  ---  F_d=KQq/d²=K4Q.4Q(2d)²  ---  F_d=16KQ²/4d²  ---  F_d=4KQ²/d²  ---  F_d/F_a=4KQ²/d² X d²/9KQ²  ---  F_d/F_a=4/9  ---  R- B

13- Quando r=3m  ---  F=2,5.10^-4N  ---  F=KQq/r²  ---  2,5.10^-4=9.10⁹.Q.Q/3²  ---  Q²=2,5.10^-13=25.10^-14  ---  Q=5.10^-7C  ---  R- E

14- Observe que, como a carga de uma partícula dobrou, a força também dobrará (2F) e como a distância dobrou, a força ficará 4 vezes menor (2F/4=F/2)  ---  F’=15/2  ---  F’=7,5N  ---  R- B

15- Cada esfera ficará com cargas de sinais opostos e de módulo  ---  Q=n.e=5.10¹⁴.1,6.10^-19  ---  Q=8.10^-5C  ---  F=KQq/d²  ---  F=9.10⁹.8.10^-5.8.10^-5/(8.10^-2)²  ---  F=9.10^-1/10^-4  ---  F=9.10³N  ---  R- B

16- Observe as figuras abaixo:

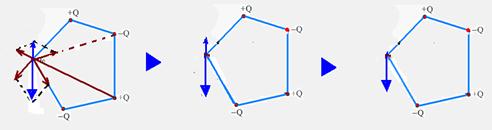
R- D

17-

R- E

18- Observe na figura abaixo que a carga –Q não pode estar à esquerda de Q e nem a direita de 4Q, pois nessas posições a

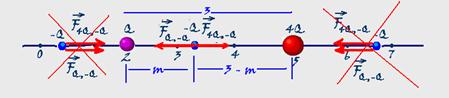
resultante não seria nula  ---  ela tem que estar entre Q e 4Q na posição da figura  ---  F_Q,_-Q=KQQ/m²  ---  F_4Q,-Q=K4QQ/(3 – m)²  ---  KQQ/m²= K4QQ/(3 – m)²  ---  1/m²=4/(3 – m)²  ---  (3 – m)²/m²=4  ---  (3 – m)/m=√4  ---  2m=3 – m  ---  m=1  ---  está na abscissa x=2 + 1=3  ---  R- C

19- a) A intensidade da força elétrica é igual à intensidade da força centrípeta  ---  F_e=F_c  ---  KQq/R²=mV²/R  ---  V=√(KQq/mR)

b) V=2πR/T  ---  2πR/T=√(KQq/mR)  ---  4π²R²/T² =KQq/mR  ---  T²=4π²R²mR  --- T=2πR√(mR/KQq)

20- a) Ou as duas são positivas ou negativas

b) Ação de q₁ e de q₃ sobre q₂  ---  F_q1q2=Kq₁q₂/r²  ---  F_q3q2=K.q₃q₂/r²  ---  Kq₁q₂/r² = K.q₃q₂/r²  ---  q₁=q₃=q  ---  ação de q₂ e de q₃ sobre q₁  ---  F_q3q1=Kq²/(2r)²  ---  F_q2q1=KQ₂q₁/r²  ---  Kq²/(2r)² = KQ₂q₁/r²  ---  q=4.2,7.10^-4  ---  q=q₁=q₂=10,8.10^-4C

c) Se você retirar um pouquinho a carga q₂ da posição de equilíbrio, ela não retorna à mesma  ---  equilíbrio instável.

21- Sendo as cargas elétricas idênticas, a força exercida por 3 sobre 2 deve ser 4 vezes maior  que a força exercida por 1 sobre 2 (metade da distância)  ---  F₁₂=4.10^-5N  ---  F₃₂=4.4.10^-5  ---  F₃₂=16.10^-5N  ---  F_R=16.10^-5 – 4.10^-5  ---  F_R=12.10^-5N  ---  R- C

22- A carga q’ deve estar entre as duas cargas a uma distância m de +q  ---  F₁=Kq’.q/m²  ---  se estiver à distância n de +4q  ---  F₂= Kq’.4q/m²  ---  F₁ = F₂  ---  Kq’.q/m² = Kq’.4q/m²  ---  (n/m)²=4  ---  n=2m  ---  n + m = 6  ---  m=2  ---  n=4  ---  R- B

23- Observe na figura abaixo que a carga pontual para ficar em equilíbrio não pode estar entre as cargas e que deve estar no ponto

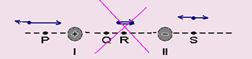
S, pois a carga positiva tem intensidade maior que a negativa  ---  R- C      

24- Observe que F_AB é 9 vezes maior que F_CB=3.10^-6N (inversamente proporcional ao quadrado da distância)  ---  F_AB=9.3.10^-6  --- 

F_AB=27.10^-6N  ---  F_R=27.10^-6 – 3.10^-6  ---  F_R=24.10^-6N  ---  R- D

25-

R- E

26- Força elétrica  ---  F_e=KQq/d²  ---  Força gravitacional  ---  F_G=GMm/d²   ---  quando a distância é 2km F_e=F_G  ---  KQq/2²=GMm/2²  ---  KQq=GMm  ---  quando a distância é 5km as massas M e m e as cargas Q e q continuam iguais, então F_e continua igual a F_G e as partículas continuam equilibradas  ---  R- B

27- Veja esquema abaixo:

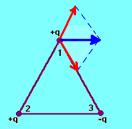
R- C

28- Força elétrica que 1 exerce em 3  ---  F₁₃=Kq₁.q₃/d²=9.10⁹.10^-6.10^-6/3²   ---   F₁₃=10^-3N  ---  como a distância e as cargas são as mesmas a força que 2 exerce em 3 também será a mesma  ---  F₂₃=10^-3N=F₁₃=F  ---  a força que q₁ exerce em q₃ é de atração e a que q₂ exerce em q₃ é de repulsão (figura).

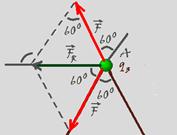
Observe que os triângulos são eqüiláteros, então a intensidade de F_R será F_R=F=10^-3N,direção horizontal e sentido para esquerda.

29- a) Como elas estão no ar, com o tempo as esferas irão se descarregando e se aproximando  ---  as forças que agem nas esferas, T intensidade da força de tração no fio,  P intensidade da força peso e F força elétrica de repulsão entre as esferas com cargas de mesmo sinal, para qualquer posição das esferas tem sempre a mesma intensidade em ambos os fios e as decomposições dessas forças serão sempre simétricas,e os ângulos serão sempre iguais.

b) Colocando as forças que agem sobre uma das esferas e que são  ---  - força de tração no fio  ---   - força peso  ---  - força

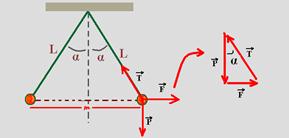
Elétrica  ---  considerando m como a distância entre as duas cargas ---  senα=(m/2)/L  ---  0,6=m/2.0,09  ---  m=0,108m  ---  no triângulo de forças  ---  tgα=F/P  ---  0,75=F/P  ---  F=0,75P  ---  KQ.Q/m²=0,75.m.g  ---  9.10⁹.Q²/(0,108)²=0,048.10  ---  Q=2,5.10^-7 C

30- Observe na figura, onde todas as forças que agem sobre a carga Q acima, da direita foram

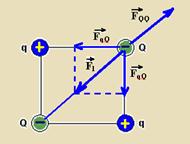
colocas, que, para que  anule  as cargas q e Q devem ter sinais opostos  ---   = +   ---  (F₁)² = (F_qQ)² + (F_qQ)²   ---  (F₁)²=KqQ/L² + KqQ/L²  ---  F₁=√2.K.q.Q/L²  ---  L – lado do quadrado  ---  F_QQ=K.Q.Q/(√2L)²  ---  F_QQ=K.Q.Q/2L²  ---  resultante nula  ---  F₁=F_QQ­  ---  

√2.K.q.Q/L² = K.Q.Q/2L²   ---  √2q=Q/2  ---  Q/q=2√2  ---  R- D

31- Figura A:

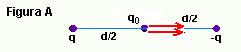
F_A=2Kqq_o/(d/2)²  ---  F_A=8Kqq_o/d²

Figura B:

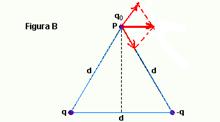
 F_B=2Kqq_o/(d/2)².cos60^o = 2Kqq_o/(d/2)².(1/2)  ---  F_B=Kqq_o/d²  ---  F_A/F_B=8Kqq_o/d² X d²/Kqq_o  ---  F_A/F_B=8

32- Depois do contato cada corpo terá carga de (1 + 5)/2= 3 C

F = k.q.Q/d² = 9.10⁹.3.3/3² = 9.10⁹ N

A força será repulsiva, pois os dois corpos apresentam a mesma natureza elétrica (são cargas positivas).

 R- D

33- Na direção horizontal para qualquer uma das esferas é verdadeiro afirmar que  ---  k.Q²/d²= T.senq  ---  na direção vertical

m.g = T.cosq  ---  dividindo as duas expressões  ---  k.Q²/(m.g.d²) = senq/cosq = 1 (pois q = 45°)  ---  d=Q√k/(mg)  --- 

d=30.10^-6_.√9.10⁸  ---  d=90.10^-2  ---  d=90cm  ---  R- B

34- a) F_N=20F_E=20Kq²/d²=20.9.10⁹.(1,6.10^-19)²/1,6.10^-15)²  ---  F_N=180.10⁹.10^-8  ---  F_N=1.800N  ---  F_N=1,8.10³N
b)F = q.E = 1,6.10^-19.2.10⁶ = 3,2.10^-13 N

35- Das informações iniciais sabemos que  ---   F = k.q.q/d²  ---  F = k.(q/d)²  ---  na configuração apresentada a força resultante sobre q₁ é  ---  Fr = Ö[F21² + F31²]  ---  Fr = Ö[(k.3q.q/d²)² + (k.4q.q/d²)]²  ---   Fr = Ö[9k².q⁴/d⁴ + 16.k².q⁴/d⁴]  ---  Fr = Ö[25k².q⁴/d⁴] = 5.k.(q/d)²  ---  Fr = 5.F  ---  R- D

36- Em cada uma das extremidades das quatro diagonais que passam pelo centro do cubo há duas cargas de mesmo módulo e de

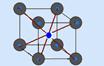
 mesmo sinal. Elas exercem na carga central (também de mesmo sinal e mesmo módulo que as dos vértices) forças de mesma intensidade e de sentidos opostos. Portanto, essas forças se equilibram, sendo então nula a resultante dessas forças. 

R- A

37-

Na situação inicial, as cargas negativas (-q), nas extremidades, repelem-se com forças de intensidade F, sendo 2 d a distância entre elas  ---  como as cargas negativas estão em equilíbrio, elas trocam forças, também, de intensidade F com a carga positiva (+Q) central, sendo d a distância do centro às extremidades  ---  a lei de Coulomb nos afirma que a intensidade das forças eletrostáticas entre duas cargas varia com o inverso do quadrado da distância entre essas cargas  ---  F=kQq/d²  ---  na situação final, a distância entre as cargas negativas foi reduzida à metade (de 2 d para d) logo, as forças de repulsão entre elas passam a ter intensidade 4 F  ---  porém,  a distância de cada carga negativa à carga central também é reduzida à metade (de d para d/2) quadruplicando, também, as forças de atração entre elas, ou seja, 4 F  ---  portanto o equilíbrio é mantido com Q’ = 1 Q  ---  R- A 

38-

Na primeira situação, as forças são atrativas e têm intensidade  ---  F=kQq/d²  (I)  ---  na segunda situação, as forças são repulsivas e têm intensidade  ---  F’=k.4Q.3q/(2d)²  ---  F’=3kQq/d² (II)  ---  comparando I com II você conclui que  F’=3F e que as forças que eram atrativas passam a ser repulsivas  ---  R- D

39- Como não foi especificada a massa da barra é considerada desprezível, como também a massa da carga suspensa  ---  as forças eletrostáticas entre as cargas têm a mesma direção da reta que passa pelos seus centros  ---  para que o sistema fique em equilíbrio as forças eletrostáticas devem ser de atração  ---   as intensidades da força de tração no fio e das forças eletrostáticas são iguais (T = F), como ilustrado na figura  ---  da figura  ---  cos30^o=d/r  ---  r=d/cos30^o  ---  r=d/(√3/2) (I)  ---  lei de Coulomb  ---  F=k_oQq/r²  

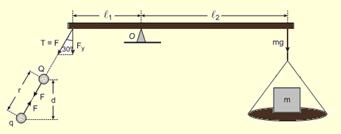
(II)  ---  (I) em (II)  --- F = k_oQq/(2d/√3)²  ---  F=3k_oQq/4d² (III)  ---  para que a barra esteja em equilíbrio a somatória dos momentos deve ser nula  ---  adotando o pólo no ponto O mostrado na figura  ---  Fcos30^oℓ₁=mgℓ₂ (IV)  ---  (III) em (IV)  ---  3k_oQq√3 ℓ₁/4d².2=mg ℓ₂  ---  3k_oQq√3 ℓ₁/8d²=mg ℓ₂  ---  q=8mgℓ₂d²/3√3k_oQℓ₁  ---  como as forças entre Q e q são de atração e, se Q é positiva, q só pode ser negativa ou vice versa  ---  R- E

40- Observe as figuras abaixo  ---  no triângulo hachurado da figura 1  ---  Pitágoras  ---  L²=d² + z²  --- 

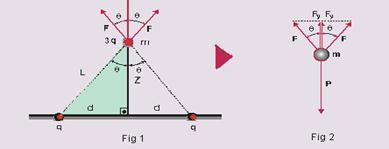
L=√(d² + z²) (I)  --- cosθ=z/L  ---  as forças de repulsão mostradas têm intensidade dada pela lei de Coulomb  ---  F=kq3q/L²  ---  F=k3q²/L² (II)  ---  (I) em (II)  ---   F=k3q²/(√d² + y²)²  ---  F= k3q²/(d² + y²)  (III)  ---  observe na figura 2 que, como a massa m está em equilíbrio a força resultante sobre ela é nula  ---  P=2F_y  ---  mg=2Fcosθ  ---  cosθ=z/L  ---  m=2F(z/L)/g (IV)  ---  (III) em (IV)  ---  m=(2/g).(k3q²/L²).(z/L)  ---  m=6kq²z/gL³  ---  m=6kq²z/g(d² + z²)^2/3  ---  R- B

41- Observe as figuras abaixo que mostram as duas situações descritas no enunciado  --- 

F=kQq/d² (I)  ---  F’=kQq/(2d)²=KQq/4d²  ---  (I)/(II)  ---  F/F’=kQq/d² x 4d²/kQq  ---  F/F’=4  ---  F’=F/4  ---  R- D

42- a) Observe na figura abaixo a imagem da carga –Q (-Q’) e a decomposição de suas velocidades e das velocidades do espelho nas direções paralelas e perpendiculares ao espelho: 

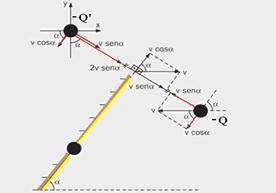
Observe na figura acima que v.senα é a velocidade com que a imagem da carga –Q se aproxima perpendicularmente do espelho e que v.cosα é a velocidade com que a imagem da carga –Q se move paralelamente ao espelho  ---  mas, também, como o espelho se aproxima da carga –Q com velocidade v.senα, a imagem de –Q se aproximará do espelho com velocidade 2v.senα  ---  como o espelho se aproxima de –Q paralelamente ao eixo x, a imagem de –Q não sofrerá deslocamento na direção paralela ao espelho  ---

Se você somar vetorialmente os vetores velocidades da imagem –Q’ e os decompondo em x e y, obterá  ---  v_x=(3vsenα).senα –

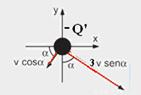
(vcosα).cosα  ---  v_x=v(3sen²α – cos²α)  ---  v_y= - (3vsenα).cosα – (vcosα).senα  ---  v_y= - 4vsenα.cosα  ---  mas sen²α=(1 – cos2α)/2 e sen2α=2senα.cosα  ---  v_x=v(3sen²α – (1 – sen²α))  ---  v_x=v(1 – 2cos2α)  ---  v_y= - 4vsen2α/2  ---  v_y= - 2vsen2α

b) Aceleração centrípeta da carga negativa  ---  intensidade  ---  a_c=v²/r  ---  direção e sentido  ---  vertical e para cima  ---  a figura mostra as forças que agem sobre a carga negativa  ---  a aceleração tangencial tem a direção do eixo x  ---  F_R=F_ex  ---

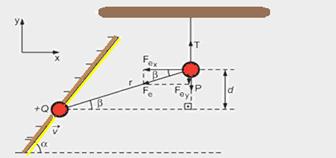
 ma=F_ecosβ  ---  F_e==kQQ/r²  ---  ma=kQQ/r²  ---  r=d/senβ  ---  ma=kQQ/(d/senβ)².cosβ  ---  a=kQ²sen²βcosβ/md²  ---  aceleração tangencial  ---  intensidade – a_t= kQ²sen²βcosβ/md²  ---  direção – eixo x  ---  sentido – contrário a x.

43- a) Do texto  ---  “Segundo todos os cálculos, as futuras usinas de fusão nuclear poderão extrair de 1 metro cúbico de água uma quantidade de energia igual à de 2 mil barris de petróleo”  ---  regra de três  ---  1 m³ – 2.10³ barris  ---  100 m³ – n barris  --- 

n=2.10³.10²  ---  n=2.10⁵ barris de petróleo  ---  como cada barril contém 1,5.10⁶ kcal, 2.10⁵ barris conterão  ---  W=2.10⁵ barris x

1,5.10⁶kcal/barril  ---  W=3,0.10¹¹ kcal=3,0.10¹⁴cal  ---  do enunciado  ---  1 BEP (Barril Equivalente de Petróleo), equivale a 1,45.10⁹ cal  ---  regra de três  ---  1 BEP – 1,45.10⁹ cal  ---  n’ BEP – 3.10¹⁴ cal  ---  n’=3.10¹⁴ cal/1,45.10⁹ cal  --- 

n’≈2,07.10⁵ BEP.

b) Do texto: “Os centros dos núcleos dos átomos de hidrogênio devem estar a 1.10^-15 metros um do outro para que ocorra a fusão”  ---  ainda do texto  ---  “essa fusão é o processo no qual dois núcleos de átomos leves (por exemplo, o hidrogênio – cujo núcleo é constituído por 1 próton com carga elétrica elementar é 1,6.10^-19C) se combinam, ou se fundem, constituindo um elemento mais pesado. Os núcleos, então, carregados positivamente, devem se aproximar suficientemente um do outro, ou seja, vencer a força de repulsão eletrostática entre eles”  ---  portanto, são dados  ---  d=1.10^-15m  ---  .|Q₁|= |Q₂|=1,6.10^-19C  ---  k=9.10⁹N.m²/C²  --- 

Lei de Coulomb  ---   F=k.|Q₁|. |Q₂|./d² = 9.10⁹.1,6.10^-19.1,6.10^-19/(1.10^-15)²   ---  F=23,04.10¹  ---  F=230,4 N.