Capacitores (Condensadores)


Capacitor ou condensador 


Capacitor ou condensador é um dispositivo elétrico que tem por função armazenar cargas elétricas e, como consequência, energia potencial elétrica.

Existem diversos tipos de capacitores (cilíndricos, esféricos ou planos), mas todos são representados por duas placas paralelas, condutoras e idênticas, bem próximas uma da outra e com

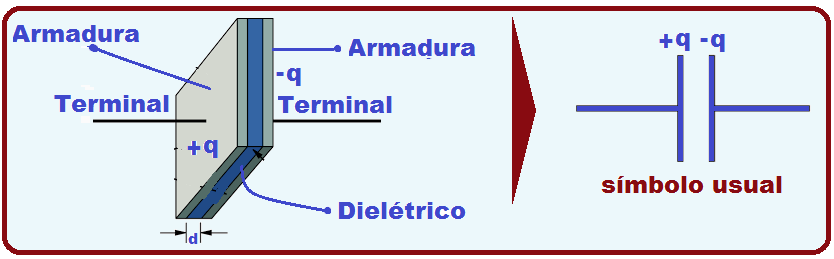
um isolante chamado dielétrico entre elas. Essas placas são denominadas armaduras do capacitor e o dielétrico (isolante) entre elas pode ser vácuo, ar, papel, mica, óleo, etc.

 

Eletrizando um capacitor (processo de carga)


Na figura, as armaduras do capacitor estão inicialmente neutras e a diferença de potencial entre as placas é nula. A seguir uma das armaduras é ligada ao polo positivo de um gerador de força eletromotriz Ɛ e a outra ao polo negativo do mesmo gerador.

A armadura ligada ao polo negativo do gerador vai sendo carregada com cargas negativas (retirando elétrons da placa de cima) e a ligada ao polo positivo do gerador vai sendo carregada com cargas positivas (acrescentando elétrons à placa de baixo) e à medida que elas vão sendo carregadas a diferença de potencial entre as placas vai aumentando até que ela se iguale à do gerador (E) e o

capacitor está carregado com tensão U = Ɛ.

Por definição a carga elétrica (Q) desse capacitor é o valor da carga da placa positiva. Lembre-se de que as cargas das placas positiva e negativa tem o mesmo módulo.

U é a diferença de potencial entre as placas positiva e negativa e Q o módulo da carga de uma das placas.


Processo de descarga de um capacitor

 


Capacitância ou capacidade eletrostática de um capacitor

 

A capacitância ou capacidade eletrostática de um capacitor representada pela letra C é característica de cada capacitor, sendo definida como a razão entre a carga Q (medida em coulomb “C” no SI) armazenada no capacitor e a diferença de potencial U (medida em volt “V”, no SI) entre as armaduras positiva e negativa, ou seja:

 No Sistema Internacional de Unidades (SI) a capacitância (capacidade) é medida em farad, cujo símbolo é F, contudo, como o farad é muito grande torna-se conveniente a utilização de submúltiplos, como o microfarad (1 μF = 10-6F), ou o picofarad (1pF=10-12F).


 

 


 Os capacitores são muito usados em circuitos eletrônicos, onde eles acumulam carga elétrica e consequentemente energia elétrica para posteriormente utilizá-la em um momento adequado, como por exemplo, em controles remoto, celulares, telefones sem fio, computadores, aparelhos de som

fornos de microondas, flash de máquina fotográfica, etc.

 

O que você deve saber, informações e dicas


 

Fatores que influem da capacitância de um capacitor


 Como a capacitância de um capacitor é uma constante característica do mesmo, ela depende de alguns fatores próprios de cada capacitor, que são:


 Área das armadura a capacitância C é proporcional à área S de cada armadura, ou seja quanto maior a área das armaduras, maior a capacitância: CS. 


A espessura (d) do dielétrico é um outro fator que influi na capacitância (são inversamente proporcionais).

Verifica-se que quanto menor for a distância (d) entre as armaduras maior será a capacitância C do componente, ou seja: C.(1/d).


 O dielétrico também é um fator determinante na capacitância, de modo que a sua natureza influencia no valor dela de modo diretamente proporcional, onde cada dielétrico tem sua característica denominada permissividade do meio, de símbolo ε.


 Então, tem-se   C= ε.S/d


 Quando o meio é o vácuo, sua permissividade é denominada εo e vale εo = 8,85.10-12 F/m.


 A constante dielétrica (K) de um meio é definida como sendo a razão entre a permissividade desse meio ε e a permissividade do vácuo εo    K = ε/εo    ε = Kεo, que, substituído em C= ε.S/d   

C= Kεo.S/d.

 

O que você deve saber, informações e dicas

 

  Quanto maior a área (S) das armaduras, maior será a capacitância e vice versa.


Quanto menor a distância (d) entre as armaduras, maior será a capacitância e vice versa.


Quanto maior for a constante dielétrica K do isolante (dielétrico) maior será a capacitância e vice versa.


 

Associação de capacitores


Associação série de capacitores


No processo de carga, quando os capacitores em série estiverem ligados ao gerador de tensão U, as cargas que saem de uma armadura serão deslocadas para a seguinte até que as cargas de todas as armaduras tenham o mesmo módulo, ou seja, Q1 = Q2 = Q3 =Q.

Observe que, se as cargas são iguais e as capacitâncias são diferentes, a diferença de potencial (tensão) também será diferente.

Você também pode calcular o capacitor equivalente como Ceq = produto/soma tomados dois a dois.

Lembre-se de que o Ceq é sempre menor que a capacitância de cada um dos capacitores associados.



Associação paralelo de capacitores


 


Cálculo do capacitor equivalente numa associação mista de capacitores

Numa associação mista o cálculo do capacitor equivalente é resolvido por etapas, substituindo os capacitores que estão em paralelo pelos equivalentes, fazendo o mesmo com os que estão em série e assim procedendo até chegar a um único capacitor equivalente final.

 

Circuitos com capacitores

 

 Lembre-se de que quando um capacitor está ligado em um circuito elétrico e já estiver carregado, por ele já não passa mais corrente elétrica e, basta retirar o ramo onde ele está inserido e resolver o circuito.

Preste muita atenção nesses dois exercícios exemplos:


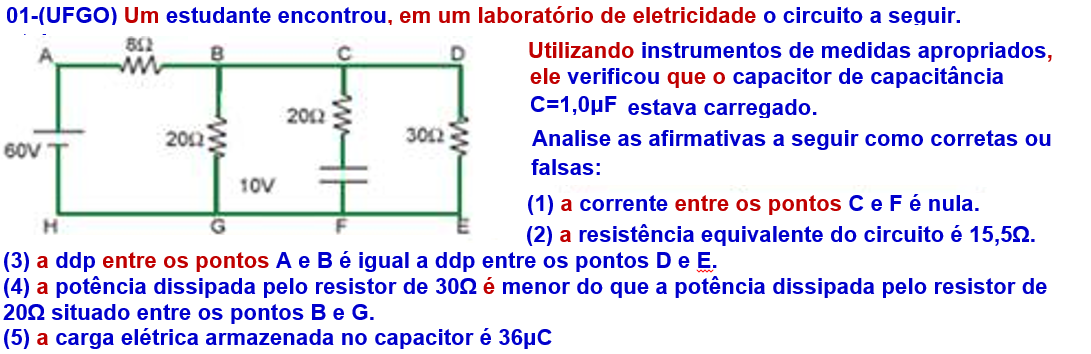
(01) Correta Depois que o capacitor está carregado não passa mais corrente no ramo onde ele está inserido.


(02) Falsa Retirando o ramo onde está o capacitor (pois ele está carregado e por ele não circula corrente) e calculando a resistência equivalente    veja sequência abaixo:


(3) Falsa Observe a sequência abaixo, onde você está retornando a partir da sequência acima:

UAB =R.i = 8.3    UAB = 24V    UDE=30.1,2    UDE = 36V.


(4) Correta P30Ω = i’’.U = 1,2.36    P30Ω = 43,2W    P20=i’.U = 1,8.36    P20Ω = 64,8 W.  (5) Observe que a diferença de potencial nos terminais do capacitor (trecho CF) é a mesma que nos trechos BG e DE e vale U=36V (estão todos em paralelo)    C = Q/U    10-6 = Q/36   

Q = 36.10-6C.

 

02- (UFLA-MG) Em quais dos circuitos a seguir é possível garantir que, transcorrido um intervalo de tempo muito longo após fechar a chave S, todas as lâmpadas estarão acesas? Suponha que a bateria satisfaça as condições necessárias para que as lâmpadas fiquem acesas e não se queimem.

a) I, II, III.              b) I, V, VI.            c) II, IV, VI.              d) III, IV, VI.               e) IV, V, VI.

Lembre-se de que, depois que o capacitor está carregado, ele interrompe o circuito e não passa corrente por ele e nem no trecho onde ele está inserido (veja figuras abaixo)

   R- D

 

 

Resolução comentada dos exercícios de vestibulares sobre

Capacitores


01-(PUC-MG) Se dobrarmos a carga acumulada nas placas de um capacitor, a diferença de potencial entre suas placas ficará:

a) inalterada.      

b) multiplicada por quatro.      

c) multiplicada por dois.     

d) dividida por quatro.        

e) dividida por dois.

 

02- (UFES) Um equipamento elétrico contém duas pilhas de 1,5V em série, que carregam um capacitor de capacitância 6,0.10-5 F.

A carga elétrica que se acumula no capacitor é, em coulombs:


03- (FUVEST-SP) Em um condensador a vácuo, de capacidade 10-3μF, ligado a um gerador de tensão 100 volts, a carga elétrica é:

a) 0,50 μC em cada uma das armaduras         

b) 0,10 μC em cada uma das armaduras          

c) 0,10 μC em uma das armaduras e - 0,10 μC na outra         

d) 0,10 μC em uma armadura e zero na outra         

e) 0,20 μC em cada uma das armaduras

 

04-(ITA-SP) O catálogo de uma fábrica de capacitores descreve um capacitor de 25V de tensão de trabalho e capacitância de 22.000μF. Se a energia armazenada nesse capacitor se descarrega em um motor, sem atrito, arranjado para levantar um tijolo de 0,5kg de massa , a altura alcançada pelo tijolo é: (considere g=10m/s2)


05- (PUC-SP) A carga de um capacitor sofre um aumento de 6.10-5C quando a diferença de potencial entre seus terminais aumenta de 50V para 60V. Esse capacitor tem capacidade:

a) 12.10-6F                       

b) 10.10-6F                         

c) 6.10-6F                            

d) 2.10-6F                        

e) 1.10-6F

 

06- (Uesb-BA) Um capacitor de um circuito de televisão tem uma capacitância  de 1,2μF. Sendo a diferença de potencial entre seus terminais de 3.000V, a energia que ele armazena é de:

 

 

07-(UFB) Baseado no gráfico abaixo, que representa a diferença de potencial nos terminais de um capacitor em função da carga

que ele armazena, calcule a carga elétrica entre suas armaduras, quando a diferença de potencial atingir 20V.

 

08-(UFLA-MG) A energia armazenada num capacitor de 10.000μF, submetido a uma diferença de potencial 16V, se descarrega num

potencial 16V, se descarrega num motor sem atrito, arranjado para erguer um bloco de 0,10kg de massa. Qual é a altura máxima atingida pelo bloco, em metros? (adote g=10m/s2)

 

09-(UFU-MG) Um capacitor, de capacidade desconhecida, tem sido usado para armazenar e fornecer energia a um aparelho de tevê. O capacitor é carregado com uma fonte de 1.000V, armazenando uma carga de 10C.

O televisor funciona num intervalo de diferença de potencial entre 80V e 260V. Quando ocorre falta de energia, liga-se o capacitor ao televisor, e este consegue funcionar durante  cerca de 5 minutos. A carga que fica armazenada no capacitor, no instante em que o televisor deixa de funcionar , é de:

a) 1C                              

b) 10C                                  

c) 2,6C                                  

d) 0,8C                                

e) 42C

 

10-(UFSM-RS) Em tempestades, quando ocorre a descarga elétrica que se caracteriza como raio,

pode-se afirmar que

a) a corrente elétrica é constante.           

b) o potencial é constante.           

c) o campo elétrico é uniforme.

d) a rigidez dielétrica do ar é rompida.  

e) a resistência do ar é uniforme.

 

(UEL-PR) Este enunciado refere-se às questões de números 11e 12.

Um capacitor plano é formado de duas armaduras planas, iguais, cada uma de área A e colocadas paralelamente a uma distância d. A capacidade eletrostática C de um capacitor plano é dada por: C= ε A/d, na qual ε varia com a natureza do dielétrico colocado entre as armaduras. Quando o meio é o vácuo ou o ar ε = 8,85.10-12F/m, sendo F (farad) a unidade de capacidade eletrostática no Sistema Internacional.
Ligando as armaduras do capacitor aos terminais de uma bateria, as armaduras ficam eletrizadas com cargas +Q e -Q, conforme está indicado no esquema:

A carga do capacitor é a carga Q da sua armadura positiva. A relação entre a carga Q e a ddp U é constante e igual à capacidade eletrostática do capacitor:C=Q/U.

 

11-(UEL-PR) Quando uma ddp de 100V é aplicada nas armaduras de um capacitor de capacidade C = 8,85.10-12F, a carga do capacitor, em coulombs, vale:

a) 8,85.10-10.                   

b) 8,85.10-8.                      

c) 8,85.10-7.                       

d) 8,85.10-6.                      

e) 8,85.10-3.


12-(UEL-PR) Se a área de cada armadura desse mesmo capacitor de capacidade 8,85.10-12F é de 200 cm2 e o dielétrico entre as armaduras é o ar, então a distância entre elas, em metros, vale:

a) 1,0.10-4.                    

b) 2,0.10-4.                         

c) 6,0.10-4.                          

d) 5,0.10-4.                       

e) 2,0.10-2.


13-(PUC-MG) Você dispõe de um capacitor de placas planas e paralelas. Se dobrar a área das placas e dobrar a separação entre

 elas, a capacitância original ficará:

a) inalterada        

b) multiplicada por dois        

c) multiplicada por quatro        

d) dividida por dois        

e) dividida por quatro

 

14-(Ufla-MG) A diferença de potencial entre as placas de um capacitor de placas paralelas de 40μF carregado é de 40V.

a) Qual a carga no capacitor? 
b) Qual a energia armazenada?
c) Sabendo-se que a distância entre as placas do capacitor é 2 mm, determine a nova capacitância se aumentarmos essa distância para 4 mm.

 

15-(UFGO-GO) Podemos entender, simplificadamente, a descarga elétrica entre duas nuvens, supondo que elas se comportem como um capacitor ideal de placas paralelas, com cargas iguais e de sinais opostos.

Considere que a distância entre essas duas nuvens seja de 150 m e que a capacitância do sistema formado pelas nuvens seja igual a 1,6.10-8F.
a) Qual a carga elétrica acumulada em cada uma dessas nuvens, para provocar uma descarga elétrica entre elas, sabendo-se que um campo elétrico de intensidade igual a 3.106V/m ioniza o ar entre as nuvens?
b) Supondo que toda a energia fornecida pela descarga elétrica fosse armazenada, quantas lâmpadas de 60W poderiam ficar acesas durante uma hora, utilizando essa energia?

 

16-(UNICAMP-SP) Um raio entre uma nuvem e o solo ocorre devido ao acúmulo de carga elétrica na base da nuvem, induzindo uma carga de sinal contrário na região do solo abaixo da nuvem.

A base da nuvem está a uma altura de 2 km e sua área é de 200 km2. Considere uma área idêntica no solo abaixo da nuvem. A descarga elétrica de um único raio ocorre em 10-3s e apresenta uma corrente de 50 kA.

Considerando εo = 9 x 10-12 F/m, responda:

a) Qual é a carga armazenada na base da nuvem no instante anterior ao raio?

b) Qual é a capacitância do sistema nuvem-solo nesse instante?

c) Qual é a diferença de potencial entre a nuvem e o solo imediatamente antes do raio?

 

17-(ITA-SP) Considere o vão existente entre cada tecla de um computador e a base do seu teclado. Em cada vão existem duas placas metálicas, uma delas presa na base do teclado e a outra, na tecla. Em conjunto, elas funcionam como um capacitor de placas planas paralelas imersas no ar. Quando se aciona a tecla, diminui a distância entre as placas e a capacitância aumenta. Um circuito elétrico detecta a variação da capacitância, indicativa do movimento da tecla. Considere então um dado teclado, cujas placas metálicas têm 40 mm2 de área e 0,7 mm de distância inicial entre si.

 Considere ainda que a permissividade do ar seja εo = 9 x 10-12 F/m,. Se o circuito eletrônico é capaz de detectar uma variação da capacitância a partir de 0,2 pF, então, qualquer tecla deve ser deslocada de pelo menos

 

18-(PUC MG)- Um capacitor de placas planas e paralelas é totalmente carregado utilizando-se uma fonte de 12 volts em três situações diferentes. Na situação A, ele permanece vazio. Em B, um dielétrico preenche metade do volume entre as placas e, em C, o mesmo dielétrico preenche todo o volume entre as placas.

Assim, com relação às cargas acumuladas, é CORRETO afirmar que:

a) as cargas em A, B e C terão o mesmo valor.       

b) A terá a maior carga e C, a menor.       

c) A terá a menor carga e C, a maior.         

d) B terá a maior carga e A, a menor.     

e) B terá a menor carga e C, a maior.

 

19-(UFPR) Considere um capacitor composto por duas placas condutoras paralelas que está sujeito a uma diferença de potencial de 100V, representado na figura a seguir:

 

Preencha os campos com V (verdadeiro) ou F (falso):

1. (__) o potencial elétrico na placa A é maior que na placa B.
2. (__) entre as placas há um campo elétrico cujo sentido vai da placa B para a placa A.
3. (__) se a capacitância deste capacitor for igual a 1,00μF, a carga elétrica em cada placa terá módulo igual a 10,0μC.
4. (__) um elétron que estiver localizado entre as placas, será acelerado em direção à placa A.
5. (__) se a distância entre as placas for reduzida à metade, a capacitância do capacitor irá duplicar.
6. (__) este capacitor pode ser usado como um elemento para armazenar energia.

 

20-(Fuvest-SP) Um capacitor é feito de duas placas condutoras, planas e paralelas, separadas pela distância de 0,50 mm e com ar entre elas. A diferença de potencial entre as placas é de 200V.

a) Substituindo-se o ar contido entre as placas por uma placa de vidro, de constante dielétrica 5 vezes maior do que a do ar, permanecendo constante a carga das placas, qual será a diferença de potencial nessa nova situação?
b) Sabendo-se que o máximo campo elétrico que pode existir no ar seco sem produzir descarga é de 0,80.106 volt/metro, determine a diferença de potencial máxima que o capacitor pode suportar quando há ar seco entre as placas.

 

21-(PUC-MG) Um capacitor ideal de placas paralelas está ligado a uma fonte de 12V. De repente, por um processo mecânico, a distância entre as placas dobra de valor. A fonte é mantida ligada em todos os instantes. Nessa nova situação, pode-se afirmar, em relação àquela inicial, que:

a) O campo elétrico dobra e a carga acumulada também          

b) O campo elétrico dobra e a carga fica reduzida à metade

c) O campo elétrico e a carga não mudam de valor                  

d) O campo elétrico e a carga ficam reduzidos à metade do valor inicial         

e) O campo elétrico fica reduzido à metade, mas a carga não muda. 

 

 22-(PUCCAMP-SP) Um capacitor de placas paralelas com ar entre as armaduras é carregado até que a diferença de potencial entre suas placas seja U.

 Outro capacitor igual, contendo um dielétrico de constante dielétrica igual a 3, é também submetido à mesma diferença de potencial. Se a energia do primeiro capacitor é W, a do segundo será:


23-(UECE-CE) Um capacitor tem uma capacitância de 8,0 × 10-11 F. Se o potencial elétrico entre suas placas for 12 V, o número de elétrons em excesso na sua placa negativa é: (considere a carga de um elétron como e=1,6 x 10-19C)

a) 9,6 × 1014                        

b) 8,0 ×1020                          

c) 6,0 × 109                        

d) 5,0 × 108                     

e) 11 x 107 

 

24-(UNICAMP-SP) Numa tela de televisor de plasma, pequenas células contendo uma mistura de gases emitem luz quando submetidas a descargas elétricas.

A figura a seguir mostra uma célula com dois eletrodos, nos quais uma diferença de potencial é aplicada para produzir a descarga. Considere que os eletrodos formam um capacitor de placas paralelas, cuja capacitância é dada por C = (ε0A)/d, onde ε0 = 8,9 × 10-12 F/m, A é a área de cada eletrodo e d é a distância entre os eletrodos.

a) Calcule a capacitância da célula.

b) A carga armazenada em um capacitor é proporcional à diferença de potencial aplicada, sendo que a constante de proporcionalidade é a capacitância. Se uma diferença de potencial igual a 100 V for aplicada nos eletrodos da célula, qual é a carga que será armazenada?

c) Se a carga encontrada no item b) atravessar o gás em 1 μs (tempo de descarga), qual será a corrente média?

 

25-(PUC-RS) Um dispositivo muito usado em circuitos elétricos é denominado capacitor, cujo símbolo é

Calcula-se a capacitância (C) de um capacitor por meio da razão entre a carga (Q) que ele armazena em uma de suas armaduras e a tensão (V) aplicada a ele, ou seja, C = Q / V.

Um capacitor A, com capacitância CA, está inicialmente submetido a uma tensão V. Então, um outro capacitor, B, de capacitância diferente CB, é conectado em paralelo com A, mantendo-se na associação a mesma tensão elétrica V. Em relação à associação dos capacitores, A e B, pode-se afirmar que

a) depois de associados, os capacitores terão cargas iguais.

b) a energia da associação é igual à energia inicial de A.

c) a energia da associação é menor do que a energia inicial de A.

d) depois de associados, o capacitor de menor capacitância terá maior carga.

e) a capacitância da associação é igual à soma das capacitâncias de A e B.

 

26-(FURG-RS) Todos os capacitores que aparecem nas figuras abaixo tem a mesma capacitância. Escolha a associação cuja capacitância equivalente é igual à de um único capacitor:


27- (UECE-CE) Considere seis capacitores de capacitância C conforme indicado na figura:

A capacitância equivalente entre os pontos P e Q é


28-(UFPA-PA) A capacidade do condensador equivalente à associação mostrada na figura é:


29-(UFLA-MG) Dado o circuito abaixo, determine o valor da capacitância equivalente, em μF.


30-(UFPE-PE) No circuito a seguir os três capacitores têm a mesma capacitância C1 = C2 = C3 = 1 μF.

Qual a diferença de potencial nos terminais do capacitor C1, em volts?


31-(UECE-CE) Três capacitores, de placas paralelas, estão ligados em paralelo. Cada um deles tem armaduras de área A, com espaçamento d entre elas. Assinale a alternativa que contém o valor da distância entre as armaduras, também de área A, de um único capacitor, de placas paralelas, equivalente à associação dos três.

a) d/3                               

b) 3d                                

c) (3d)/2                              

d) (2d)/3                                

e) 5d/4

 

32-(UERJ-RJ) Para a segurança dos clientes, o supermercado utiliza lâmpadas de emergência e rádios transmissores que trabalham com corrente contínua.

Para carregar suas baterias, no entanto, esses dispositivos utilizam corrente alternada. Isso é possível graças a seus retificadores que possuem, cada um, dois capacitores de 1.400 μF, associados em paralelo. Os capacitores, descarregados e ligados a uma rede elétrica de tensão máxima igual a 170 V, estarão com carga plena após um certo intervalo de tempo t.

Considerando t, determine:

a) a carga elétrica total acumulada;

b) a energia potencial elétrica total armazenada.

 

33-(UFPE-PE) Três capacitores C1 = C2 = 1,0 μF e C3 = 3,0 μF estão associados como mostra a figura.

A associação de capacitores está submetida a uma diferença de potencial de 120 V fornecida por uma bateria. Calcule o módulo da diferença de potencial entre os pontos B e C, em volts.

 

34-(ITA-SP) A figura 1 mostra um capacitor de placas paralelas com vácuo entre as placas, cuja capacitância é Co. Num determinado instante, uma placa dielétrica de espessura d/4 e constante dielétrica K é colocada entre as placas do capacitor, conforme a figura 2. Tal modificação altera a capacitância do capacitor para um valor C1. Determine a razão Co/C1.

a) (3K + 1)/4K         

b) 4K/(3K + 1)           

c) (4 + 12K)/3           

d) 3/(4 + 12K)           

e) 1/(4 + 12K)

 

35-(UFJF-MG) Na figura abaixo, cada capacitor tem capacitância C = 11μ F. Entre os pontos A e B existe uma diferença de potencial de 10 V. Qual é a carga total armazenada no circuito?

a) 3,0.10-5 C.                    

b) 4,0.10-5 C.                     

c) 5,0.10-5 C.                      

d) 6,0.10-5C.                    

e) 7,0.10-5 C.

 

36-(UEPG-PR) Sobre capacitância elétrica e capacitores, assinale o que for correto.

01) A capacitância de um condutor isolado é inversamente proporcional ao potencial a que ele está submetido. 

02) Para descarregar um capacitor, basta estabelecer a ligação elétrica entre as duas armaduras, por meio de um condutor. 

04) Capacitores associados em série adquirem, todos, a mesma carga. 

08) Reduzindo-se a distância entre as placas de um capacitor plano, sua capacitância aumenta.  

16) A capacitância de um condutor esférico é diretamente proporcional ao seu raio. 

 

37-(UFC-CE) Dois capacitores desconhecidos são ligados em série a uma bateria de força eletromotriz ε, de modo que a carga final de cada capacitor é q. Quando os mesmos capacitores são ligados em paralelo à mesma bateria, a carga total final da associação é 4q. Determine as capacitâncias dos capacitores desconhecidos.

 

 38-(FUNREI-MG) Considere o circuito abaixo, onde E=10V, C1=2μF, C2=3μF e C3=5μF.

De acordo com essas informações, é INCORRETO afirmar que a carga:

a) em C1 é 10μC                   

b) em C2 é 15μC                 

c) fornecida pela bateria é 10μC                

d) em C3 é 25μC

 

39-(UNIUBE-MG) No circuito de capacitores, esquematizado a seguir, temos uma fonte idealε=

100V, e capacitâncias C1 =2,0μF e C2 = 3,0μF. Após carregados os capacitores C1 e C2, suas cargas serão, respectivamente, em μC:

a) 200 e 300                     

b) 48 e 72                    

c) 120 e 120                        

d) 60 e 60                       

e) 80 e 90


40-(PUC-MG) Ache a energia armazenada no capacitor C=4,0μF, sendo R=1Ω

 


41-(Uesb-BA) No circuito da figura, o gerador G tem f.e.m. igual a 6V. O capacitor C, inicialmente descarregado e de capacitância 2.10-6F, está ligado em série com a lâmpada L.

Nessas condições, fechando-se a chave K:

01) a ddp nos terminais do capacitor permanece nula.                     

02) a lâmpada ficará acesa indefinidamente. 
03) o capacitor estará em curto circuito.                                           

04) o capacitor adquire 3.10-6C de carga elétrica. 
05) a energia potencial elétrica do capacitor será igual a 3,6.10-5J.

 

42-(MACKENZIE-SP) Considere o circuito abaixo alimentado por duas baterias  que fornecem 10V, cada uma. Ele contém quatro resistores de 1Ω cada um. O capacitor de capacitância 1μF foi conectado ao circuito estando inicialmente neutro.

Nessas condições, o capacitor fica eletrizado com carga, em μC, igual a:


43-(ITA-SP) O circuito da figura é composto de duas resistências, R1 = 1,0 × 103 Ω e R2 = 1,5 × 103 Ω, respectivamente, e de dois capacitores de capacitâncias C1 = 1,0 × 10-9 F e C2 = 2,0 × 10-9 F, respectivamente, além de uma chave S, inicialmente aberta. Sendo fechada a chave S, a variação da carga ∆Q no capacitor de capacitância C1, após determinado período, é de

a) - 8,0 × 10-9 C.               

b) - 6,0 × 10-9 C.                 

c) - 4,0 × 10-9 C.                 

d) + 4,0 × 10-9 C.              

 e) + 8,0 × 10-9 C. 

 

44-(ITA-SP) No circuito mostrado na figura abaixo, a força eletromotriz da bateria é E=10V e sua resistência interna é r=1Ω.

 Sabendo-se que R=4,0Ω e C=2,0μF, e que o capacitor já se encontra totalmente carregado, quais as afirmações são corretas

I. A indicação do amperímetro é 0 A. 

II. A carga armazenada no capacitor é 16μC.

III. A tensão entre os pontos a e b é 2,0V.

IV. A corrente na resistência R é 2,5 A.


45-(UNICAMP-SP) Dado o circuito elétrico esquematizado na figura, obtenha:

a) a carga no condensador enquanto a chave ch estiver aberta; 
b) a carga final no condensador após o fechamento da chave.

 

46-(MACKENZIE-SP) Um capacitor, inicialmente descarregado, é ligado a um gerador elétrico de

resistência interna 2Ω, adquirindo uma carga de 2,4.10-11C. A corrente de curto circuito no gerador é 6,0 A. A capacidade elétrica do capacitor é:


47-(ITA-SP) Duas baterias de fem 10V e 20V, respectivamente, estão ligadas a duas resistências de 200Ω e 300μΩ e com um capacitor de 2μF, como mostra a figura.

Sendo Q a carga do capacitor e P a potência total dissipada depois de estabelecido o regime estacionário . conclui-se que:

a) Q=14μC; P=0,1W      

b) Q=28μC; P=0,2W      

c) Q=28μC; P=10W          

d) Q=32μC; P=0,1W          

e) a) Q=32μC; P=0,2W

 

48-(UFG-GO) Um desfibrilador externo, usado para reversão de paradas cardíacas, provoca a descarga rápida de um capacitor através do coração, por meio de eletrodos aplicados ao tórax do paciente. Na figura a seguir, vê-se o gráfico de descarga de um capacitor de capacidade C, inicialmente 100% carregado, através de um resistor de resistência R, em função do tempo, o qual é dado em termos da constante de tempo τ = RC. Observe que, a cada constante de tempo τ, a carga no capacitor reduz-se à metade.

Supondo que o capacitor perca 87,5% de sua carga em 3 ms e que a resistência entre os eletrodos seja de 50 Ω, determine, para uma d.d.p. inicial entre as placas de 5 kV:

a) a corrente média entre os eletrodos, nesse intervalo de 3 ms;

b) a energia inicial armazenada no capacitor.

 

49-(UNICAMP-SP)

Em 1963, Hodgkin e Huxley receberam o prêmio Nobel de Fisiologia por suas descobertas sobre a geração de potenciais elétricos em neurônios. Membranas celulares separam o meio intracelular do meio externo à célula, sendo polarizadas em decorrência do fluxo de íons. O acúmulo de cargas opostas nas superfícies interna e externa faz com que a membrana possa ser tratada, de forma aproximada, como um capacitor.

a) Considere uma célula em que íons, de carga unitária, e=1,6.10-19C, cruzam a membrana e dão origem a uma diferença de potencial elétrico de  80 mV . Quantos íons atravessaram a membrana, cuja área é A=5,0.10-5 cm2, se sua capacitância por unidade de área é 0,8.10-6F/cm2?

b) Se uma membrana, inicialmente polarizada, é despolarizada por uma corrente de íons, qual a potência elétrica entregue ao conjunto de  íons no momento em que  a  diferença de potencial for  20 mV e  a corrente for 5.108 íons/s, sendo a carga de cada íon e=1,6.10-19C?

 

50-(FUVEST-SP)

O fluxo de íons através de membranas celulares gera impulsos elétricos que regulam ações fisiológicas em seres vivos. A figura abaixo ilustra o comportamento do potencial elétrico V em diferentes pontos no interior de uma célula, na membrana celular e no líquido

extracelular.

O gráfico desse potencial sugere que a membrana da célula pode ser tratada como um capacitor de placas paralelas com distância entre as placas igual à espessura da membrana,  d = 8 nm. No contexto desse modelo, determine

a) o sentido do movimento - de dentro para fora ou de fora para dentro da célula - dos íons de cloro (Cl-) e de cálcio (Ca2+), presentes nas soluções intra e extracelular;

b) a intensidade  E do campo elétrico no interior da membrana;

c) as intensidades FCl e FCa  das forças elétricas que atuam, respectivamente, nos íons Cl+ e Ca2+ enquanto atravessam a membrana;

d) o valor da carga elétrica Q na superfície da membrana em contato com o exterior da célula, se a capacitância C do sistema for igual a 12 pF.

 

51-(AFA)

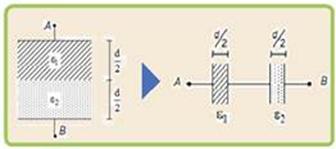
A região entre as placas de um capacitor plano é preenchida por dois dielétricos de permissividades ε1 e ε2, conforme ilustra a figura a seguir

Sendo S a área de cada placa, d a distância que as separa e U a ddp entre os pontos A e B, quando o capacitor está totalmente carregado,

o módulo de carga Q de cada placa é igual a

 

 

Resolução comentada dos exercícios de vestibulares sobre

Capacitores


01- C=Q/U  ---  como a capacitância C é constante para cada capacitor  ---  se dobrar Q, U também deverá dobrar  ---  R- C


02- Como as pilhas estão associadas em série  ---  E=U=1,5 + 1,5  ---  U=3,0V  ---  C=Q/U  ---  6,0.10-5=Q/3,0  ---  Q=18.10-5C  ---  Q=1,8.10-4C  ---  R- D


03- C=Q/U  ---  10-3.10-3=Q/102  ---  Q=10-6.102  ---  Q=10-4=10-1.10-3=0,1.10-3C  ---  Q=0,1μC  ---  R- C


04- Energia liberada pelo capacitor ao se descarregar  ---  W=C.U2/2=22.10-3.(25)2/2  ---  W=6,875J  ---  essa energia foi utilizada para elevar o tijolo de massa 0,5kg a uma altura h e vale  ---  W=mgh  ---  6,875=0,5.10.h  ---  h=6,875/5  ---  h=1,375m  ---  R- C


05- Como a capacitância C é uma constante característica de cada capacitor, as variações entre Q e U são proporcionais  ---  C=ΔQ/ΔU  ---  C=6.10-5/(60 – 50)  ---  C=6.10-6F  ---  R- C


06- energia armazenada  ---  W=C.U2/2=1,2.10-6.(3.103)2/2  ---  W=1,2.10-6.9.106 /2 ---  W=5,4J  ---  R- B


07- A capacitância é constante e vale  ---  C=Q/U=60.10-6/3=180.10-6/9  ---  C=20μF  ---  quando U=20V  ---  C=Q/U  ---  20.10-6 = Q/20  ---  Q=400μC


08- Energia liberada pelo capacitor ao se descarregar  ---  W=C.U2/2=10-2.(16)2/2   ---  W=1,28J  ---  essa energia é utilizada para elevar o bloco de h  ---  W=m.g.h  ---  1,28=0,10.10.h  ---  h=1,28m  ---  

R- C


09- O televisor deixa de funcionar no início dos 5 minutos quando a tensão é de 80V  ---  a capacidade é constante e vale  ---  C=Q/U=10/1.000  ---  C=10-2F  ---  C=Q/U  ---  10-2=Q/80  ---  Q=80.

10-2  ---  Q=0,8C  ---  R- D


10- R- D  ---  veja teoria


11- C= Q/U  ---  8,85.10-12=Q/102  ---  Q=8,85.10-10C  ---  R- A

12- C= Kεo.A/d  ---  como o dielétrico é o ar  ---  K=1  ---  A=200cm2=2.102.10-4=2.10-2m2  ---  C= Kεo.A/d ---  8,85.10-12= 1.8,85.10-12.2.10-2/d  ---  d=2.10-2m  ---  R- E 


13- dobrando a área, a capacitância C também dobra  ---  dobrando d, a capacitância C fica reduzida à metade  ---  R- A


14- a) C=Q/U  ---  40.10-6=Q/40  ---  Q=1.600.10-6  ---  Q=1,6.10-3C

b) W=C.U2/2=40.10-6.(40)2/2  ---  W=3,2.10-2J

c) dobrando d, a capacitância C cai pela metade  ---  C=40μF/2  ---  C=20μF


15- a) d=150m  ---  E=3.106V/m  ---  U=E.d=3.106.150  ---  U=450.106V  ---  C=Q/U  ---  1,6.10-8=Q/450.106  ---  Q=720.10-2  ---  Q=7,2C
b) energia fornecida pela descarga  ---  W=C.U2/2=1,6.10-8.(450.106)2/2  ---  W=1,62.109J  ---  P=W/Δt=1,62.109/3.600  ---  P=45.104W  ---  1 lâmpada - 60W  ---  n lâmpadas – 45.104W  ---  n=45.104/60=0,75.104  ---  n=7.500 lâmpadas


16- a) i=Q/Δt  ---  50.103=Q/10-3  ---  Q=50C

b) C= εo.A/d=9.10-12.200.106/2.103  ---  C=9,0.10-7F

c) C=Q/U  ---  9.10-7=50/U  ---  U=50/9.107  ---  U=5,6.107V


17- 

R- B


18- Quanto mais dielétrico, maior será C e consequentemente maior U e maior Q, pois como C é constante, Q e U são diretamente proporcionais  ---  R- C


19- 1. Verdadeira  ---  o potencial da placa A (positiva) é maior que o da placa B (negativa).

2. Falsa  ---  o sentido do campo elétrico no interior das placas é das cargas positivas para as negativas.

3. Falsa  ---  C=Q/U  ---  10-6=Q/100  ---  Q=10-4C=100μC

4. Verdadeira  ---  cargas de mesmo sinal se repelem e cargas de sinais opostos se atraem.

5. Verdadeira  ---  a capacitância é inversamente proporciona à distância entre as placas

6. Verdadeira  ---  essa é a principal característica dos capacitores

R- 1.V; 2.F; 3.F; 4.V; 5.V; 6.V 

20- a) Como a capacitância C é diretamente proporcional à constante dielétrica, C ficará também 5 vezes maior  ---  C=Q/U  ---  como Q é a mesma, para C ficar 5 vezes maior, U deverá ficar 5 vezes menor  ---  U=200/5  ---  U=40V

b) U=8.105V  ---  d=0,5mm=5.10-4m  ---  U=E.d=8.105.5.10-4  ---  U=40.101  ---  U=400V

21- A ddp U é a mesma, pois a fonte é sempre a mesma  ---  antes  ---  E=U/d  ---  E=12/d  ---  depois  ---  E’=12/2d  ---  E’=E/2  ---  o campo elétrico cai pela metade  ---  C=εA/d  ---  Q.U= εA/d  ---  Q= εA/d.U  ---  observe nessa expressão que a única grandeza variável é d e que é inversamente proporcional a Q, ou seja, se d dobrar, Q ficará reduzida à metade  ---  R- D


22- A capacitância C é diretamente proporcional à à constante dielétrica K  ---  como ela é triplicada C fica 3 vezes maior  ---  U permanece constante  ---  W=C.U2/2  ---  assim a nova energia armazenada ficará 3 vezes maior  ---  R- C


23- C=Q/U  ---   8.10-11=Q/12  ---  Q=96.10-11C  ---  regra de três  ---  1 e – 1,6.10-19C  ---  n e – 96.10-11C  ---  n=6,0.109 eletrons  ---  R- C

24-


25- R- E  ---  veja teoria


26- Veja sequência abaixo:

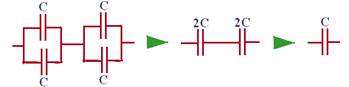
R- D


27- Os dois últimos capacitores estão em circuito aberto e não participam  ---  observe a seqüência abaixo  --- 

R- C


28- Observe a seqüência abaixo:

R- B


29-

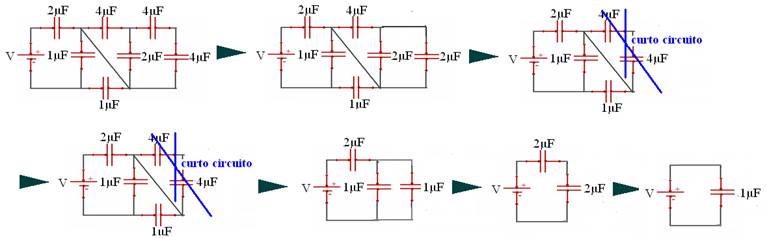
R- C


30- Os capacitores C2 e C3 estão ligados em paralelo e a  capacitância equivalente dos dois  é Ceq = 2C. Portanto a diferença de potencial no capacitor C1=C será o dobro. Ficamos então com 60 V no capacitor C1  ---  R- 60V


31- O capacitor equivalente de área A e distância entre as placas d’ que está em paralelo com os três capacitores C de área A e distância d vale Ceq=3C  ---  εA/d’=3εA/d  ---  d’=d/3  ---  R- A


32- a)Como estão em paralelo  ---  Ceq=1.400.10-6 + 1.400.10-6  ---  Ceq=2,800.10-6F  ---  Ceq=Q/U  ---  2.800.10-6=Q/170  ---  Q=0,476C

b) W=C.U2/2=2.800.10-6.(170)2/2  ---  W=40.460.000.10-6  ---  W=40,46J


33- C1 e C2 estão em paralelo  ---  C’=2,0μF  ---  C’ está em série com C3=3μF  ---  veja figura abaixo  ---

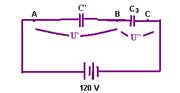
como C’ está em série com  C3, eles possuem a mesma carga Q  ---  C’=Q/U’  ---  U’=Q/2.10-6  ---  U’’=Q/3.10-6  ---  U’ + U’’=120  ---  Q/2.10-6 +

Q/3.10-6=120 (I)  ---  C’=Q/U’  ---  Q=2.10-6U’ (II)  ---  (II) em (I)  ---  2.10-6U’2.10-6 +  2.10-6U’=120  ---  U’ + 2/3U’=120  ---  3U’+ 2U’=360  ---  U’=360/5  ---  U’=72V  ---  U’’=120 – 72  ---  U’’=48V 


34- R- A


35- Observe na seqüência abaixo o cálculo da capacitância do capacitor equivalente  --- 

 

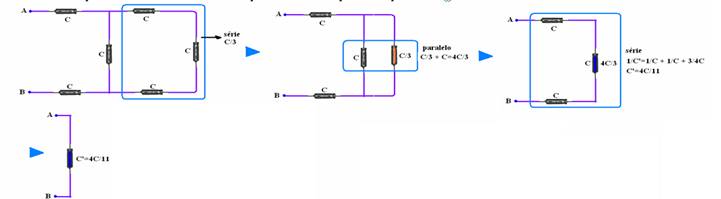
C’=Ceq=4C/11=4.11.10-6/11  ---  Ceq=4.10-6F  ---  Ceq=Q/U  ---  4.10-6=Q/10  ---  Q=4.10-5C  ---  R- B


36- Todas estão corretas  ---  veja teoria 


37- A capacitância de um capacitor é dada por C = q/U de onde vem => U = q/C

No circuito em série  ---  ε = U1 + U2  ---  ε = (q/C1) + (q/C2) => ε/q = (1/C1) + (1/C2)   ---   ε/q=(C1 + C2)/(C1 .C2)

No circuito em paralelo  ---  ε = U1  ---  ε = q1/C1 => q1 = ε.C1  ---  ε = U2  ---  ε = q2/C2 => q2 = ε.C2  ---  q1 + q2 = ε.C1 + ε.C2 = ε.(C1 +C2) = 4q   ---  (C1 +C2) = 4q/ε => C1 = 4q/ ε - C2  ---  então  ---  ε/q = (C1 + C2)/(C1 .C2)  ---  ε/q = (4q/ε)/(C1 .C2) => C1 .C2 = 4q2/ε

C1 .C2 = 4q2/ε  ---  (4q/ε - C2) .C2 = 4q2/ε   ---   C22 - (4q/ε).C2 + (4q2/ε2) = 0   ---   C2 = 2q/ε  ---  e ainda  ---  C1 = 4q/ε  - C2 = 4q/ε  - 2q/ε  ---   C1 = 2q/ε 


38- C1  e C2 estão em paralelo  ---  C’=(2 + 3).10-6  ---  C’=5.10-6F  ---  observe a figura abaixo e note que, como as capacitâncias de C3

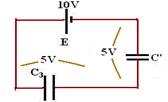
 e de C’ são iguais, eles estão sob mesma ddp U=5V  ---  C’=Q/U  ---  5.10-6=Q/5  ---  Q=25.10-6C  ---  C1=Q1/U  ---  2.10-6=Q1/5  ---  Q1=10.10-6C  ---  Q2=C2.U=3.10-6.5  ---  Q2=15.10-6C  ---  Q3=C3.U=5.10-6.5  ---  Q3=25.10-6C  ---  1/Ceq=C’ série com C3=5/2.10-6C  ---  Ceq=2,5.10-6C  ---  Ceq=Q/U  ---  2,5.10-6=Q/5  ---  Q=12,5.10-6C  ---  R- C


39- Associados em série  ---  Ceq=2.3/(2 + 3)μC  ---  Ceq=1,2.10-6C  ---  Ceq=Q/U  ---  1,2.10-6=Q/100  ---  Q=120.10-6C  ---  Q= 120μC  ---  como estão em série essa carga é a mesma para os dois capacitores  ---  R- C


40- Depois que o capacitor está carregado, não passa mais corrente por ele e o circuito fica conforme esquema abaixo: 

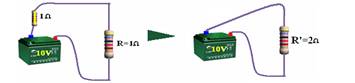
R’=U/i  ---  2=10/i  ---  i=5 A  ---  cálculo da ddp nos terminais do capacitor  ---  R=U/i  ---  1-U/5  ---  U=5V  ---  W=C.U2/2  --- 

W=4.10-6.(5)2/2  ---  W=50μJ


41- 01- Falsa  ---  o capacitor fica com ddp de 6V

02- Falsa  ---  a lâmpada ficará acesa até que o capacitor fique carregado

03- Falsa  ---  não há curto circuito, existe a lâmpada

04- Falsa  ---  C=Q/U  ---  2.10-6=Q/6  ---  Q=12.10-6C

05- Correta  ---  W=C.U2/2=2.10-6.36/2  ---  W=3,6.10-5J

R- a correta é a 05


42- Refazendo o circuito:

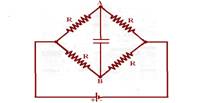
Observe que se trata de uma ponte de Wheatstone em equilíbrio, pois o produto das resistências opostas é nulo e, nessas condições o potencial em A é igual ao potencial em B  ---  UAB=0  ---  R- A


43-

R- B


44-   I. Correta  ---  o capacitor carregado interrompe a corrente no ramo do circuito onde está inserido o capacitor e o amperímetro.

  II. Correta  ---  i=10/5  ---  i=2 A  ---  R=U/i  ---  4=U/2  ---  U=8V  ---  C=Q/U  ---  2.10-6=Q/8  ---  Q=16μC.

 III. Falsa  ---  é 8V  ---  veja II.

 VI. Falsa  ---  é 2 A  ---  veja II.

R- B


45- a) Chave aberta  ---  observe na seqüência abaixo que a tensão nos terminais do capacitor com a chave aberta é U=30V  --- 

C=Q/U  ---  3.10-6=Q/30  ---  Q=90μC

b) Chave fechada  --- 

Req=U/i  ---  20=30/i  ---  i=1,5 A  ---  o capacitor está no ramo onde tem o resistor de 10Ω e a tensão em seus terminais vale  ---

R=U/i  ---  10=U/1,5  ---  U=15V  ---  C=Q/U  ---  3.10-6=Q/15  ---  Q=45μC


46- A corrente de curto circuito num gerador é fornecida por icc=E/r  ---  6=E/2  ---  E=U=12V  ---  C=Q/U=2,4.10-11/12  --- 

C=2.10-12C  ---  C=2pF  ---  R- E


47- Tirando o capacitor e aplicando a lei de Pouillet  ---  200i + 300i -20 +10=0  ---  i=1/50 A  ---  cálculo da tensão U nos terminais do capacitor  ---  U=E – r.i=20 – 300.1/50  ---  U=14V  ---  Q=C.U=2.10-6.14=28.10-6C  ---  Q=28μC  ---  P=R.i2=500.(1/50)2  ---  P=0,2W  ---  R- B


48- a) Como o capacitor perde 87,5% da sua carga em 3 ms, significa 3ms correspondem a 3τ (τ = R.C), então τ = 1 ms:

 

τ = R . C  ---   1 x 10-3 = 50 . C >>> C = 2 x 10-5 F  ---  Q = C . U >>> Q = 2 x 20-5 x 5 x 103 = 0,1 C  ---  Im = ΔQ/Δt = (0,875 x 0,1) / (3 x 10-3) = 29,2 A

b) A energia armazenada no capacitor é dada por E = (C . U2) / 2

E = [2 x 10-5 x (5 x 103)2] / 2   ---   E = 250 J

 

49- a) Cálculo da capacitância C da membrana de área 5,0.10-5cm2, se cada cm2 de área tem capacitância de 0,8.10-6F  ---  regra de três  ---  1 cm2– 0,8.10-6F  ---  C=5.10-5.0,8.10-6  ---  C=4.10-11 F  ---  seja (n) a quantidade de íons, cada um com carga e=1,6.10-19C, então a quantidade de carga total (Q) que atravessará a membrana vale  ---  Q=n.e=n.1,6.10-19  ---  Q=1,6.10-19.n  ---  definição de capacitância  ---  C=Q/U  ---  4.10-11 = 1,6.10-19.n/80.10-3  --- n=2,0.107 íons.

b) Potência elétrica entregue ao conjunto de  íons para despolarizar a membrana  ---  P=i.U=(Q/∆t).U=(n./∆t).e.U  ---  P=5.108.1,6.10-19.20.10-3---  P=1,6.10-12 W.


50- a) Cargas negativas (íons negativos – Cl-) deslocam-se para pontos de maior potencial, do interior para o exterior da célula  ---  cargas positivas  (íons positivos – Ca2+) deslocam-se para pontos de menor potencial, do exterior para o interior da célula.

b) No interior da membrana (interior do capacitor), pelo gráfico a ddp U=(64.10-3 – 0)=64.10-3m  ---  U=E.d  --- 64.10-3=E.8.10-9  --- E=8,0.106V/m ou N/C.

c) Força elétrica sobre os íons Cl-  ---  FCl=|q|.E=1.1,6.10-19.8.106  ---  FCl=1,28.10-12N  ---  força elétrica sobre os íons Ca2+  ---  FCa=|q|.E=2.1,6.10-19.8.106  ---  FCl=2,56.10-12N.

d) Pela definição de capacitância, sendo Q a carga elétrica na superfície externa da membrana  ---  C=Q/U  ---  12.10-12=Q/64.10-3  --- Q=7,68.10-13C.


51- Observe que, da maneira como eles estão ligados você pode considerá-los como associados em série  ---  a expressão matemática da capacitância de um capacitor é C=ε.S/D  ---  no caso,

C1=ε1.S/(d/2) e C2=ε2.S/(d/2)  ---  na associação série de capacitores a capacidade do capacitor equivalente é dada por  ---  Ceq=produto/soma=C1.C2/(C1 + C2)  ---  Ceq= [ε1.S/(d/2). ε2.S/(d/2)]/[ε1.S/(d/2) + ε2.S/(d/2)]  ---Ceq=2.ε1.ε2.S/d(ε1 + ε2)  ---  Q=Ceq.U  ---  Q=2.ε1.ε2.S/d(ε1 + ε2).U  ---  R- C