Segunda lei de Ohm (Resistividade)

Através de pesquisa, Ohm descobriu que a resistência elétrica de um condutor, mantida a temperatura constante, depende de três fatores:

A resistência elétrica R é diretamente proporcional ao comprimento L do fio.

Considere um fio metálico condutor de mesmo material (por exemplo,cobre Cu) e mesma área de seção transversal S, submetido a uma diferença de potencial constante U.

Experimentalmente constata-se que R é diretamente proporcional a L, ou seja, a um comprimento duplo corresponde uma resistência dupla, a uma comprimento triplo, resistência tripla, etc.

A resistência elétrica R é inversamente proporcional à área se seção reta transversal (S).

No esquema abaixo, os fios são de mesmo material e mesmo comprimento L, mas com seções retas (espessuras) de áreas S diferentes.

Nesse caso, a resistência R é inversamente proporcional a S, ou seja, que, à área de seção transversal dupla, a resistência cai pela metade; à área tripla, resistência três vezes menor, etc..

A resistência elétrica R depende do material que constitui o corpo.

Fios de mesmo comprimento L e mesma área de seção transversal S, mas, de materiais diferentes, apresentam diferentes resistências elétricas.

À essa dependência do valor da resistência em relação ao material que constitui o resistor, chama-se resistividade do material e representa-se pela letra grega ρ “rô”.

Pode-se representar matematicamente os três fatores acima pela equação:

Dedução da unidade da resistividade (ρ) no sistema internacional de unidades (SI)

O que você deve saber, informações e dicas

Quando você afirma, que a resistividade do alumínio no SI é ρ_Al= 2,8.10⁸Ωm, você quer dizer que um condutor de alumínio, com 1m de comprimento e 1m² de área de seção reta transversal, tem uma resistência de R = 2,8.10⁸Ω, mantida a temperatura constante, no nosso exemplo a 20^oC.

Tabela com os valores da resistividade de alguns materiais

Reostatos

Reostatos são resistores variáveis cuja finalidade é adaptar a intensidade da corrente elétrica a valores desejados.

Tipos de reostatos:

Os principais tipos de reostatos são reostato de cursor variando o cursor você está

variando a resistência (figura 1) reostato de pontos em cada posição da chave a resistência elétrica tem um determinado valor (figura 2).

Exercícios de vestibulares com resolução comentada sobre

Segunda lei de Ohm (Resistividade)

01-(UEFS-BA) Dois condutores metálicos, A e B de mesmo comprimento e constituídos do mesmo material, possuem área de seção transversal respectivamente igual a SA e SB e estão em equilíbrio térmico entre si. Pode-se afirmar que o condutor A apresenta, em relação ao condutor B, igual:

a) massa

b) resistividade elétrica

c) resistência elétrica

d) condutividade elétrica

02-(UFC-CE) Duas lâmpadas, L1 e L2, são idênticas, exceto por uma diferença: a lâmpada L1 tem

um filamento mais espesso que a lâmpada L2. Ao ligarmos cada lâmpada a uma tensão de 220 V, observaremos que:

a) L1 e L‚ terão o mesmo brilho.

b) L1 brilhará mais, pois tem maior resistência.

c) L2 brilhará mais, pois tem maior resistência.

d) L2 brilhará mais, pois tem menor resistência.

e) L1 brilhará mais, pois tem menor resistência.

03-(UNITAU-SP) Um condutor de secção transversal constante e comprimento L tem resistência elétrica R. Cortando-se o fio pela metade, sua resistência elétrica será igual a:

04-(FGV-RJ)-Um fio de cobre tem um raio igual a r, uma resistência R e comprimento L. Se o raio do fio for duplicado e o

comprimento reduzido à metade, o novo valor da resistência vale:

05-(UEL-PR) Para variar a potência dissipada por aparelhos tais como chuveiros, aquecedores elétricos, lâmpadas incandescentes, são projetados resistores com diferentes resistências elétricas. Em um projeto, um fio condutor de comprimento l e de diâmetro da seção transversal D teve reduzidos à metade tanto o seu diâmetro quanto o seu comprimento (conforme está representado na figura). O que acontecerá com a resistência R' do novo fio, quando comparada à resistência R do fio original?

a) R/R’=1/4

b) R/R’=1/8

c) R/R’=1/2

d) R/R’=4

e) R/R’=2

06-(UFSC) Assinale a(s) proposição(ões) CORRETA(S).

(01). Para a maioria dos metais a resistividade diminui quando há um aumento na temperatura.

(02). Para um condutor ôhmico um aumento de tensão corresponde a um aumento proporcional de corrente elétrica.

(04). Para dois condutores de mesmo material e mesmo comprimento, sendo que um tem o dobro da área de seção do outro, teremos uma mesma intensidade de corrente se aplicarmos a mesma tensão sobre ambos.

(08). A dissipação de energia por efeito Joule num resistor depende do sentido da corrente e independe da tensão aplicada sobre ele.

(16). Ao se estabelecer uma corrente elétrica num fio metálico submetido a certa tensão contínua, teremos prótons se movendo do pólo positivo ao negativo.

(32). Os metais geralmente são bons condutores de eletricidade e de calor.

07-(UFSM-RS) Dois fios condutores do mesmo material e do mesmo comprimento, com seções retas de áreas A e 2A, submetidos

à mesma diferença de potencial e à mesma temperatura, dissipam, por efeito Joule, respectivamente, as potências P1 e P2, com P1/P2 valendo:

08-(UESB-BA) Um condutor cilíndrico de comprimento L tem resistência elétrica R. Sendo estirado até um comprimento 2L,

mantendo o mesmo volume, a resistência elétrica será igual a:

09-(UECE-CE) O alemão Georg Simon Ohm (1787 – 1854) verificou experimentalmente que a resistência elétrica de um objeto depende do material que o constitui, das dimensões e de sua temperatura.

Um condutor sólido cilíndrico tem raio R e comprimento L. Outro condutor cilíndrico de mesmo material, comprimento L, e raio R é oco ao longo de seu eixo. O raio interno é r. Estando os dois condutores à mesma temperatura, a relação entre as resistências Rmaciço/Roco é:

a) (r² – R²)/ r²

b) 1 – (r²/R²)

c) r²/R²

d) (R - r )²/R²

10-(UERJ-RJ) Considere dois cabos elétricos de mesmo material e com as seguintes características:

Sabe-se que o peso do cabo 2 é o quádruplo do peso do cabo 1.

Calcule o valor da resistência elétrica R₂.

11-(PUC-PR) Na figura abaixo, é mostrado um resistor de chuveiro com regulagem para duas temperaturas.

O fabricante especifica que quando 220 volts forem aplicados entre os terminais A e B do resistor sob fluxo contínuo de água, 5500 watts de potência elétrica serão convertidos em calor, que aquecerá a água passando pelo resistor.

Analise as afirmativas:

I. Quando os 220 volts são aplicados entre os terminais A e C, a corrente elétrica no resistor é menor e a água sai mais fria do chuveiro.

II. Quando os 220 volts são aplicados entre os terminais A e C, a potência elétrica convertida em calor é maior e a água sai mais quente do chuveiro.

III. Quando a chave seletora de temperatura do chuveiro está na posição “morna”, os 220 volts estão aplicados nos terminais A e B. Com a chave na posição “quente”, os 220 volts estão aplicados nos terminais A e C.

Marque a alternativa que contêm todas e apenas as afirmações corretas.

A) I e III.

B) Apenas II.

C) Apenas I.

D) Apenas III.

E) II e III.

12-(UNIFESP-SP) Você constrói três resistências elétricas, RA, RB e RC, com fios de mesmo comprimento e com as seguintes características:

I. O fio de RA tem resistividade 1,0 . 10-6 Ω . m e diâmetro de 0,50 mm.

II. O fio de RB tem resistividade 1,2 . 10-6 Ω . m e diâmetro de 0,50 mm.

III. O fio de RC tem resistividade 1,5 . 10-6 Ω . m e diâmetro de 0,40 mm.

Pode-se afirmar que:

a) RA > RB > RC.

b) RB > RA > RC.

c) RB > RC > RA.

d) RC > RA > RB.

e) RC > RB > RA.

13-(UNICAMP-SP)) O tamanho dos componentes eletrônicos vem diminuindo de forma impressionante. Hoje podemos imaginar componentes formados por apenas alguns átomos. Seria esta a última fronteira? A imagem a seguir mostra dois pedaços microscópicos de ouro (manchas escuras) conectados por um fio formado somente por três átomos de ouro. Esta imagem, obtida recentemente em um microscópio eletrônico por pesquisadores do Laboratório Nacional de Luz Síncrotron, localizado em Campinas, SP, demonstra que é possível atingir essa fronteira.

a) Calcule a resistência R desse fio microscópico, considerando-o como um cilindro com três diâmetros atômicos de comprimento. Lembre-se de que, na Física tradicional, a resistência de um cilindro é dada por: R=ρ.L/A, onde ρé a resistividade, L é o comprimento do cilindro e A é a área da sua seção transversal. Considere a resistividade do ouro ρ= 1,6.10-8 Ωm, o raio de um átomo de ouro 2,0.10-10 m e aproxime π=3,2.
b) Quando se aplica uma diferença de potencial de 0,1V nas extremidades desse fio microscópico, mede-se uma corrente de 8,0.10-6A. Determine o valor experimental da resistência do fio. A discrepância entre esse valor e aquele determinado anteriormente deve-se ao fato de que as leis da Física do mundo macroscópico precisam ser modificadas para descrever corretamente objetos de dimensão atômica.

14-(UFC-CE) Um pássaro pousa em um dos fios de uma linha de transmissão de energia elétrica. O fio conduz uma corrente

elétrica i= 1000A e sua resistência, por unidade de comprimento, é de 5,0.10^-5 Ω/m. A distância que separa os pés do pássaro, ao longo do fio, é de 6,0 cm. A diferença de potencial, em milivolts (mV), entre os seus pés é:

a) 1,0. b) 2,0. c) 3,0. d) 4,0. e) 5,0.

15-(UNICAMP-SP) Uma lâmpada incandescente (100W,120V) tem um filamento de tungstênio de

comprimento igual 31,4cm e diâmetro 4,0.10-2mm. A resistividade do tungstênio à temperatura ambiente é de 5,6.10-8Ωm.

a) Qual a resistência do filamento quando ele está à temperatura ambiente?

b) Qual a resistência do tungstênio com a lâmpada acesa?

16-(UNIFESP-SP) A linha de transmissão que leva energia elétrica da caixa de relógio até uma

residência consiste de dois fios de cobre com 10,0 m de comprimento e secção reta com área 4,0 mm² cada um. Considerando que a resistividade elétrica do cobre é ρ = 1,6.10^-8 Ω.m,

a) calcule a resistência elétrica r de cada fio desse trecho do circuito.

b) Se a potência fornecida à residência for de 3.300 W a uma tensão de 110 V, calcule a potência dissipada P nesse trecho do circuito.

17-(ITA-SP) Um resistor Rx é mergulhado num reservatório de óleo isolante. A fim de estudar a variação da temperatura do reservatório, o circuito de uma ponte de Wheatstone foi montado, conforme mostra a figura 1.

Sabe-se que Rx é um resistor de fio metálico de 10 m de comprimento, área da seção transversal de 0,1 mm2, e resistividade elétrica ρo de 2,0 × 10^-8 Ω m, a 20 °C. O comportamento da resistividade ρ versus temperatura t é mostrado na figura 2. Sabendo-se que o resistor Rx foi variado entre os valores de 10 Ω e 12 Ω para que o circuito permanecesse em equilíbrio, determine a variação da temperatura nesse reservatório.

18-(UFF-RJ) Um dos hábitos de higiene que proporciona uma vida saudável é o banho diário. Na

possibilidade de se utilizar um chuveiro elétrico, esse hábito pode se tornar desagradável quando, nos dias frios, a água é pouco aquecida.
Para melhorar o aquecimento sem alterar o fluxo de água e a posição da chave seletora, uma pessoa retira 1/6 do comprimento do resistor.
Considerando que a tensão nos terminais do chuveiro se mantém constante, é correto afirmar que a razão entre as potências antes e após a redução do comprimento do resistor é:

19- (MACKENZIE-SP) Um fio A tem resistência elétrica igual a duas vezes a resistência elétrica de um outro fio B. Sabe-se que o fio A tem o dobro do comprimento do fio B e sua seção transversal têm raio igual à metade do raio da seção transversal do fio B. A relação ρA/ρB entre a resistividade do material do fio A e a resistividade do material do fio B é:

20-(MACKENZIE-SP) Deseja-se alimentar a rede elétrica de uma casa localizada no sítio ilustrada a seguir:

Em A, tem-se o ponto de entrada do sítio, que “recebe” a energia da rede pública e, em B, o ponto de entrada da casa. Devido à irregularidades no terreno, as possibilidades de linhas de transmissão de A até B apresentadas pelo eletricista foram a linha 1 (linha pontilhada) e a 2 (linha cheia); porém, somente uma será instalada. Com uma mesma demanda de energia, independentemente da opção escolhida e utilizando-se fio de mesmo material, deseja-se que no ponto chegue a mesma intensidade de corrente elétrica. Para que isso ocorra, o diâmetro do fio a ser utilizado na linha 1, deverá ser igual:

a) ao diâmetro do fio utilizado na linha 2

b) a 0,6 vezes o diâmetro do fio utilizado na linha 2

c) a 0,72 vezes o diâmetro do fio utilizado na linha 2

d) a 1,2 vezes o o diâmetro do fio utilizado na linha 2

e) 1 1,44 vezes o diâmetro do fio utilizado na linha 2

21-(PUC-MG) Os chuveiros elétricos permitem alterar a temperatura da água sem alterar o seu fluxo, fornecendo-lhe mais ou menos calor. Esses equipamentos possuem uma chave seletora que altera o valor da resistência elétrica,

modificando-lhe o comprimento. Considere que, ao mover a chave seletora da posição A para a posição B, o comprimento da resistência tenha sido reduzido em 20%.

Considerando-se que se mantiveram inalteradas as demais condições, é CORRETO afirmar:

a) A temperatura da água não vai se alterar.

b) A potência do chuveiro aumentou 25% e a água sairá mais quente.

c) A potência irá diminuir 20% e a água sairá mais fria.

d) Não se pode fazer nenhuma previsão sem saber se o chuveiro opera com 110V ou 220V.

22-(UDESC-SC) A tabela a seguir fornece os comprimentos, as áreas da seção transversal e as resistividades para fios de cinco materiais diferentes. A resistência desses fios não depende da tensão aplicada.

A partir desses dados, indique a alternativa que contém o fio referente ao material que transforma mais energia por unidade de tempo quando todos estão individualmente submetidos à mesma diferença de potencial em suas extremidades.

23-(UDESC-SC) A tabela a seguir apresenta algumas propriedades dos fios de cobre comumente utilizados em circuitos e instalações elétricas.

Considerando que a resistividade do cobre a 20 °C é igual a 1,7 × 10-8 Ω m, e as informações fornecidas na tabela acima, resolva as questões a seguir:

a) Calcule a resistência por unidade de comprimento de um fio de cobre de calibre 12.

b) Para a montagem de um circuito elétrico são necessários 10 m de fio de cobre. A resistência máxima oferecida pelo fio não poderá ser maior do que 2,0 x 10-2 Ω para o bom funcionamento do circuito. Determine qual o diâmetro mínimo de fio que pode ser utilizado para a montagem do circuito e identifique qual o calibre do fio.

24-(UDESC-SC) Sobre as características de resistores exclusivamente ôhmicos, analise:

I. a potência elétrica dissipada pelo resistor depende do valor da intensidade da corrente elétrica que o atravessa;

II. a resistividade é uma característica do material do qual o resistor é feito, e quanto maior for o valor da resistividade, mantidas as dimensões espaciais, menos condutor é esse resistor;

III. a classificação como resistor ôhmico se dá pelo fato de que nesses resistores, os valores da diferença de potencial aplicada e da intensidade de corrente elétrica quando multiplicados, geram sempre um mesmo valor constante;

IV. A potência elétrica total de um circuito elétrico sob diferença de potencial não nula e constituída apenas por resistores é igual à soma das potências dissipadas individualmente em cada resistor, independentemente de como eles são associados.

Está correto apenas o contido em:

25- (UEPG-PR)

A respeito da resistência elétrica apresentada pelos condutores e de resistores elétricos, assinale o que for correto.

01) Resistor é um dispositivo elétrico especialmente construído para impedir a passagem da corrente elétrica.

02) Dobrando o comprimento de um condutor e mantendo a sua área de secção transversal, sua resistência dobra, porém sua resistividade se reduz à metade.

04) Lâmpadas ligadas em série tem suas intensidades luminosas reduzidas à medida que no circuito se acrescentam novas lâmpadas.

08) A resistência elétrica de um condutor depende de suas dimensões, da sua condutividade e da sua temperatura.

26-(PUC-RS)

Durante um experimento realizado com um condutor que obedece à lei de Ohm, observou-se que o seu comprimento dobrou, enquanto a área da sua secção transversal foi reduzida à metade. Neste caso, se as demais condições experimentais permanecerem inalteradas, pode-se afirmar que a resistência final do condutor, em relação à resistência original, será

a) dividida por 4.

b) quadruplicada.

c) duplicada.

d) dividida por 2.

e) mantida.

27-(UFSCAR-SP)

As lâmpadas incandescentes foram inventadas há cerca de 140 anos, apresentando hoje em dia praticamente as mesmas características físicas dos protótipos iniciais. Esses importantes dispositivos elétricos da vida moderna constituem-se de um filamento metálico envolto por uma cápsula de vidro. Quando o filamento é atravessado por uma corrente elétrica, se aquece e passa a brilhar. Para evitar o desgaste do filamento condutor, o interior da cápsula de vidro é preenchido com um gás inerte, como argônio ou criptônio.

a) O gráfico apresenta o comportamento da resistividade do tungstênio em função da temperatura. Considere uma lâmpada incandescente cujo filamento de tungstênio, em funcionamento, possui uma seção transversal de 1,6.10-2 mm2 e comprimento de 2 m. Calcule qual a resistência elétrica R do filamento de tungstênio quando a lâmpada está operando a uma temperatura de

3 000 oC.

b) Faça uma estimativa da variação volumétrica do filamento de tungstênio quando a lâmpada é desligada e o filamento atinge a temperatura ambiente de 20 oC. Explicite se o material sofreu contração ou dilatação.

Dado: O coeficiente de dilatação volumétrica do tungstênio é 12.10-6 (ºC)-1.

28-(PUC-MG)

SUPERCONDUTIVIDADE

O termo supercondutividade se refere à capacidade que alguns materiais têm de conduzir a corrente elétrica sem que ocorram perdas de energia na forma de calor.

O QUE FAZ UM CONDUTOR SER SUPER?

A história dos semicondutores já é quase centenária e começa em 1911 com o físico Heike Kamerling Onnes, que observou o fenômeno no mercúrio resfriado a 4,2 K. Em 1995, compostos de cobre dopados com tálio exibiram o fenômeno da supercondutividade a temperaturas de 138 K a pressões ambientes e até a temperaturas de 164 K em altas pressões.

Em um condutor comum, os elétrons da corrente elétrica são continuamente espalhados pelos íons metálicos do fio, perdendo energia, que aquece o fio, fenômeno conhecido como efeito joule. Em um supercondutor, esses elétrons combinam-se e formam os chamados pares de Cooper, unidos por uma interação atrativa, e movem-se sem haver espalhamento.

(Texto adaptado de Scientific American Brasil, ano 8 numero 88, págs. 48-55.)

Considere uma linha de transmissão de energia elétrica em um fio condutor com diâmetro de 2 cm e comprimento de 2000 m

comprimento de 2000 m percorrido por uma corrente de 1000 A. Se essa transmissão fosse feita através de um supercondutor, a cada hora, seria evitada a perda de uma energia de, aproximadamente, igual a:

Dado: ρ =1,57 x 10^-8 Ω.m

a) 3,6 x 10⁸ J

b) 1,4 x 10⁹ J

c) 7,2 x 10⁸ J

d) 8,5 x 10¹⁰ J

29-(PUC-MG)

SUPERCONDUTIVIDADE

O termo supercondutividade se refere à capacidade que alguns materiais têm de conduzir a corrente elétrica sem que ocorram perdas de energia na forma de calor.

O QUE FAZ UM CONDUTOR SER SUPER?

(Texto adaptado de Scientific American Brasil, ano 8 numero 88, págs. 48-55.)

Essa energia perdida seria capaz de aquecer até 100ºC, aproximadamente quantos quilogramas de água inicialmente a 28 ºC?

Dado: c = 4200 J/kg.oC

a) 3,5 x 10³kg

b) 1,2 x 10³ kg

c) 4,5 x 10⁵ Kg

d) 1,0 x 10⁶ kg

30-(ENEM-MEC) A resistência elétrica e as dimensões do condutor

A relação da resistência elétrica com as dimensões do condutor foi estudada por um grupo de cientistas por meio de vários experimentos de eletricidade. Eles verificaram que existe proporcionalidade entre: resistência (R) e comprimento (ℓ), dada a mesma secção transversal (A); resistência (R) e área da secção transversal (A), dado o mesmo comprimento (ℓ) e

comprimento (ℓ) e área da secção transversal (A), dada a mesma resistência (R).

Considerando os resistores como fios, pode-se exemplificar o estudo das grandezas que influem na resistência elétrica utilizando as figuras seguintes.

As figuras mostram que as proporcionalidades existentes entre resistência (R) e comprimento (ℓ), resistência (R) e

área da secção transversal (A), e entre comprimento (ℓ) e área da secção transversal (A) são, respectivamente,

a) direta, direta e direta.

b) direta, direta e inversa.

c) direta, inversa e direta.

d) inversa, direta e direta.

e) inversa, direta e inversa.

31-(UFU-MG)

Um fio de comprimento e possui uma dada resistividade elétrica. Quando esse fio é conectado nos terminais de uma bateria, ele é percorrido por uma corrente i. O fio é cortado ao meio e colocado em paralelo nos terminais da mesma bateria.

A corrente que circula por cada metade do fio, nesse caso, será de:

32-(ITA-SP)

Um fio condutor é derretido quando o calor gerado pela corrente que passa por ele se mantém maior que o calor perdido pela superfície do fio (desprezando a condução de calor pelos contatos). Dado

que uma corrente de 1 A é a mínima necessária para derreter um fio de seção transversal circular de 1 mm de raio e 1 cm de comprimento, determine a corrente mínima necessária para derreter um outro fio da mesma substância com seção transversal circular de 4 mm de raio e 4 cm de comprimento.

a) 1/8 A

b) 1/4 A

c) 1 A

d) 4 A

e) 8 A

Resolução comentada dos exercícios de vestibulares sobre

Segunda lei de Ohm (Resistividade)

01- Como são de mesmo material, possuem a mesma resistividade elétrica --- R- B

02- A resistência R é inversamente proporcional à espessura (S) --- maior espessura, menor R, maior corrente i --- brilha mais --- R- E

03- Mesmo fio --- mesma resistividade ρ --- mesma S --- L cai pela metade --- R é diretamente proporcional a L --- R também cai pela metade --- R- B

04- R é inversamente proporcional à área de seção reta transversal S --- S=πr² --- a nova área ficará 4 vezes maior, pois R está ao quadrado, e a resistência R ficará 4 vezes menor --- R é diretamente proporcional ao comprimento L --- se L é reduzido à metade, R também será reduzido à metade --- R’=R/4.2=R/8 --- R- D

05- Reduzindo o comprimento à metade --- R fica 2 vezes menor --- reduzindo o diâmetro (r/2) à metade --- R fica 4 vezes maior --- R’=(1/2 x 4)R --- R’=2R --- R- C

06- (01) Quando a temperatura da maioria dos metais aumenta, há um aumento no movimento vibratório de seus átomos e moléculas, que dificultam a passagem da corrente elétrica diminuindo-a, o que provoca um aumentando de sua resistência elétrica. Como a resistividade é diretamente proporcional à intensidade da corrente elétrica, ela também aumenta --- Falsa.

(02) Correta --- resistor ôhmico, R constante --- U é diretamente proporcional a i.

(04) Falsa --- Se a área S dobra, a resistência R cai pela metade.

(08) Falsa --- W=P_o.Δt=i.U.Δt --- i é a intensidade da corrente que independe de seu sentido e, observe na fórmula, depende da tensão U.

(16) Falsa --- corrente elétrica é um movimento ordenado de elétrons.

(32) Verdadeira --- veja teoria.

R- (02 + 32)=34

07- R₁=R --- R é inversamente proporcional à S --- R₂=R/2 --- P₁=U²/R --- P₂=U²/(R/2) --- P₂=2U²/R --- P₁/P₂=U²/R x R/2U² --- P₁/P₂=1/2 --- R- B

08- Sendo o mesmo material, a resistividade ρ é a mesma --- quando ele é estirado, como mantém o mesmo volume, o comprimento

passa a 2L e a nova espessura a S₁ --- V=S.L --- V=S₁.L₁ --- S.L=S₁.2L --- S₁=S/2 --- R=ρ.L/S (I) --- R₁=ρ.L₁/S₁ --- R₁=ρ.2L/S/2 --- R₁=4ρ.L/S (II) --- comparando (II) com (I) --- R₁=4R --- R- A

09- Maciço --- R_maciço=ρ.L/πR² --- oco --- S_maior=π(R)² --- S_menor=π( r )² --- S=π.R²– π.r² --- S=π( R² – r²) --- a expressão da resistência fica --- R_oco=ρ.L/π(R² – r²) --- R_maciço/R_oco= ρ.L/πR² x π(R² – r²)/ρL --- R_maciço/R_oco=(R² – r²)/R²= 1 – r²/R² --- R- B

10- P₂=4P₁ --- m₂=4m₁ --- mesmo material, mesma densidade --- d=m₁/V₁ --- d=m₂/V₂ --- m₁/V₁=4m₁/V₂ --- V₂=4V₁ --- V₁=S₁.L₁=S₁.25 --- V₂=S₂.L₂=S₂.75 --- V₂=4V₁ --- 75S₂=4.25.S₁ --- S₂=4S₁/3 --- R₁=ρL₁/S₁ ---

4= ρ.25/S₁ --- ρ=4.S₁/25 --- R₂= ρ.L₂/S₂=4.S₁/25.75/(4S₁)/3 --- R₂=75.3/25 --- R₂=9Ω

11- I. Entre A e C --- maior resistência --- menor corrente --- menor potência --- aquece menos --- correta

II. Falsa --- veja I.

III. Falsa --- quente é entre B e C (menor R, maior potência, aquece mais) e não entre A e C.

R- C

12- R_A=ρ_A.L/π(r_A)²=10^-6.L/π(0,25)² --- R_A=16.10^-6L/π --- R_B=ρ_B.L/π(r_B)²=1,2.10^-6.L/π.(0,25)² --- R_B=19,2.10^-6L/π --- R_C=ρ_C.L/π(r_C)²=1,5.10^-6.L/π.(0,2)² --- R_C=37,5.10^-6L/π --- R- E

13- a) L=3.(4.10^-10)=12.10^-10m --- R=ρ.L/A --- R=ρ.L/π.(r)² = 1,6.10^-8.12.10^-10/3,2.(2.10^-10)² --- R=19,2.10^-18/12,8.10^-20 --- R=1,5.10²Ω

b)R=U/i=10^-1/8.10^-6 --- R=0,12.10⁵ --- R=1,2.10⁴Ω

14- A resistência por unidade de comprimento=ρ/S --- R=ρL/S=5.10^-5.6.10^-2=30.10^-7 --- R=3.10^-6Ω --- R=Ui --- 3.10^-6=U/10³ --- U=3.10^-3 A --- R- C

15- a) R=ρL/S=5,6.10^-8.31,4.10^-2/π(4/2.10^-5)² --- R=175,84.10^-10/3,14.4.10^-10=175,84.10^-10/12,56.10^-10 --- R=14Ω

b) P_o=U²/R --- 100=(120)²/R --- R=14.400/100 --- R=144Ω (observe que, com a lâmpada acesa a temperatura aumenta, aumentando assim o movimento vibratório dos átomos e moléculas do tungstênio.o que dificulta a passagem da corrente elétrica, aumentando portanto a resistência).

16- a) R=ρL/S=1,6.10^-8.10/4.10^-6=1,6.10^-7/4.10^-6 --- R=0,4.10^-1 --- R=0,04Ω

b) Corrente que chega à residência --- P_o=i.U --- 3.300=i.110 --- i=30 A --- da caixa de relógio até a residência existem dois fios --- R=2.0,04=8.10^-2Ω --- P_o=R.i²=8.10^-2.900 --- P_o=72W

17- A ponte de Wheatstone é um dispositivo que permite determinar o valor de resistência elétrica desconhecida --- R_x=ρL/S --- R_x varia de 10Ω até 12Ω --- R_x=10Ω --- 10=ρ₁L/S (I) --- R_x=12Ω --- 12= ρ₂L/S (II) --- subtraindo (II) de (I) --- 2=( ρ₂ - ρ₁).L/S --- 2=Δρ.L/S --- 2=Δρ.10/0,1.10^-6 --- Δρ=2.10^-8Ωm --- pelo gráfico --- regra de três --- Δρ (2.10^-8Ωm) – Δt _oC --- (ρ – ρ_o) (0,8.10^-8Ωm) – 89^oC --- 0,8.10^-8.Δt=160.10^-8 --- Δt=200^oC

18- R_antes=R(6R/¨) --- comprimento 6 vezes menor R_depois=5R/6 --- P_oantes=U²/R --- P_odepois=U²/5R/6=6U²/5R --- P_oantes/P_odepois=U²/R x5R/6U² --- P_oantes/P_odepois=5/6 --- R- E

19-R_A=2R_B --- L_A=2L_B --- AS=S_B/4 --- ρ=R.S/L --- ρ_A=R_A.S_A/L_A --- ρ_A=2R_B.(S_B/4)/2L_B --- ρ_A/ρ_B= 2R_B.(S_B/4)/2L_Bx L_B/R_B.S_B --- ρ_A/ρ_B=R_BS_B/2L_B x L_B/R_BS_B --- ρ_A/ρ_B=1/2 --- R- B

20- Para que a corrente seja a mesma em cada linha, as duas devem ter a mesma resistência elétrica --- R=ρL/S ---

S=π( r )² =π.(d/2 )² --- S=πd²/4 --- R₁=ρ(72 + 72)/π.(d₁²/4)=4.144/πd₁² --- R₂=ρ100/π(d₂²/4)=4.100/ πd₂² ---

R₁=R₂ --- 4.144/πd₁²=4.100/ πd₂² --- (d₁/d₂)²=144/100 --- d₁/d₂=12/10 --- d₁/d₂=1,2

21- R₁=R --- R₂=0,8R --- P₁=U²/R --- P₂=U²/0,8R --- P₁/P₂=U²/R x 0,8R/U² --- P₂=P₁/0,8 --- P₂=1,25P₁ --- P₂=125%P₁ --- R- B

22- W=P_o.Δt=(U²/R).Δt --- maior potência, menor resistência, consome mais energia --- menor resistência – substituindo os valores de cada alternativa na equação R=ρ.L/S, chega-se à resposta --- R- C

23- a) R=ρL/S=1,7.10^-8.1/3,5.10^-6 --- R=0,486.10^-2 --- R=4,86.10^-3Ωm

b) R=ρL/S --- 2.10^-2=1,7.10^-8.10/S --- S=1,7.10^-7/2.10^-2=85.10^-7m² --- S=8,5mm² --- S=π.r² --- 8,5=3,14.r² --- r=√2,71 --- r=1,6mm --- d=2.r=2.1,6 --- d=3,2mm --- calibre 8

24- I- Correta --- P_o=R.i² --- quanto maior i, maior P_o

II- Correta --- R=ρL/S --- quanto maior ρ, maior R e menor i

III- Falsa --- é a razão U/i que é constante e não o produto U.i

IV- Correta --- Falsa --- depende do tipo de associação (série, paralelo ou mista)

R- D

25- (01) Errada. Resistor é um dispositivo elétrico para CONTROLAR a intensidade da corrente elétrica.

(02) Errada. A resistividade de um material só depende dele próprio e de sua temperatura.

(04) Correta. Quando se acrescentam novas lâmpadas em série, aumenta-se a resistência equivalente do conjunto, diminuindo a corrente. Como P = Ri², reduz-se também a potência dissipada em cada uma delas, diminuindo as intensidades luminosas.

(08) Correta. De acordo com a Segunda Lei de Ohm, a resistência depende: do material de que é feito o condutor, das dimensões do condutor e da temperatura.

R- (04 + 08) = 12

26- Sendo ρ a resistividade do material, L o comprimento do condutor e A a área de sua secção transversal, a segundo lei da Ohm nos dá que a resistência (R) desse condutor é --- R=ρL/A --- dobrando o comprimento e reduzindo à metade a área de sua secção transversal, a nova resistência passa a ser --- R’=(ρ2L)/A/2=4(ρL/A) --- R’=4R --- R- B

27- a) Dados --- A = 1,6.10^-2 mm2 = 1,6.10^-8 m² --- L = 2 m --- do gráfico --- quando a temperatura é T = 3.000 °C, a resistividade é ρ = 8.10^-7 Ω.m --- segunda lei de Ohm --- R= ρL/S=8.10^-7.2/1,6.10^-8 --- R=100Ω

b) Dados --- λ = 12.10^-6 °C^-1 --- T’ = 20 °C --- T = 3.000 °C --- 3.000 °C, o volume inicial é --- V_o = S.L = 1,6.10^-8. 2 ---

V_o= 3,2.10^-8 m³ --- variação volumétrica --- ΔV = V_o.λ.(T’ – T) = 3,2.10^-8.12.10^-6 (20 – 3.000) --- ΔV= – 1,1.10^-9 m³=-1,1mm³

--- o sinal (–) indica que o material sofreu contração.

28- Dados --- D = 2 cm = 2.10^-2 m --- L = 2.10³ m --- i = 10³ A; --- Δt = 1 h = 3,6.10³ s.

A resistência da linha é dada pela 2ª lei de Ohm --- R=ρL/S --- área da secção transversal --- S= πr² =π(D/2)² --- S=πD²/4 ---

R=ρL/S=4ρL/(πD²/4)=4(1,57.10^-8).(2.10³)/3,14.(2.10^-2)² --- R=0,1Ω --- P_o=R.i² --- P_o=ΔW/Δt --- ΔW=P_o.Δt ---

ΔW=R.i².Δt --- ΔW=0,1.(10³)².3,6.10³ --- ΔW=3,6.10⁸J --- R- A

R- A

29- Dados --- c = 4.200 J --- ΔT = (100 – 28) = 72 °C --- Q = ΔW = 3,6.10⁸ J --- equação do calor sensível --- Q = m c ΔT --- m = Q/cΔt=3,6.10⁸/4,2.10³.72 --- m=1,2.10³kg --- R- B

30- Baseado nas figuras:

(1) Mantendo-se a secção transversal constante e dobrando-se o comprimento (ℓ) do fi o, a resistência (R) dobra --- então, a proporcionalidade entre ℓ e R é direta.

(2) Mantendo-se o comprimento constante e dobrando-se a área da secção transversal (A), a resistência (R) fica dividida por dois --- então, a proporcionalidade entre A e R é inversa.

(3) Mantendo-se a resistência constante e dobrando-se o comprimento (ℓ) do fio, a área da secção transversal (A)

dobra. Assim, a proporcionalidade entre ℓ e A é direta.

R- C

31- As figuras 1 e 2 ilustram a situação descrita.

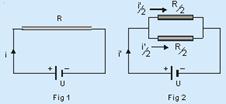
Considere que na Fig 1 a resistência elétrica do fio é R e a corrente é i --- sendo U a ddp fornecida pela bateria, aplicando a 1ª lei de Ohm --- R=U/i --- i=U/R --- de acordo com a 2ª lei de Ohm, a resistência elétrica é diretamente proporcional ao comprimento Então, ao se cortar o fio ao meio, a resistência elétrica de cada pedaço é metade da resistência do fio inteiro ---

R₁=R₂=R/2 --- colocando-se os dois pedaços em paralelo como na Fig 2, a resistência do circuito é --- R’=(R/2)/2 --- R’=R/4 --- corrente i’ no circuito --- U’=U/R’=U/(R/4) --- U’=4U/R --- U’=4i --- correntes nos pedaços --- i₁=i₂=i’/2=4i/2 --- i₁=i₂=2i --- R- A

32-