Conservação da Quantidade de Movimento

Sistema isolado de forças externas Um sistema formado por vários corpos ou pontos materiais é considerado isolado, quando:

sobre ele não atuam forças externas.

sobre ele agem forças externas, mas a intensidade da força resultante (soma vetorial de todas as forças externas que agem sobre ele) é nula.

as forças externas existem, mas suas intensidades são muito pequenas (praticamente desprezíveis) quando comparadas com as forças internas, que são muito grandes.

Princípio da Conservação da Quantidade de Movimento

Quando um sistema é isolado de forças externas, sua força resultante tem intensidade nula e consequentemente o impulso dessa força é nulo, pois I = F_R.∆t = 0. ∆t = 0.

Como I = Q_depois – Q_antes 0 = Q_depois Q_antes Q_antes = Q_depois.

Sendo a quantidade de movimento grandeza vetorial, a relação abaixo representa o princípio da conservação da quantidade de movimento:

O que você deve saber, informações e dicas

O centro de massa de um corpo é o ponto onde toda a massa do corpo está concentrada para o cálculo de vários efeitos dinâmicos. Ele não precisa necessariamente coincidir com o seu centro geométrico (centro de gravidade), podendo estar inclusive fora do corpo.

No caso, por exemplo, de um atleta, o movimento do centro de massa é semelhante ao movimento de

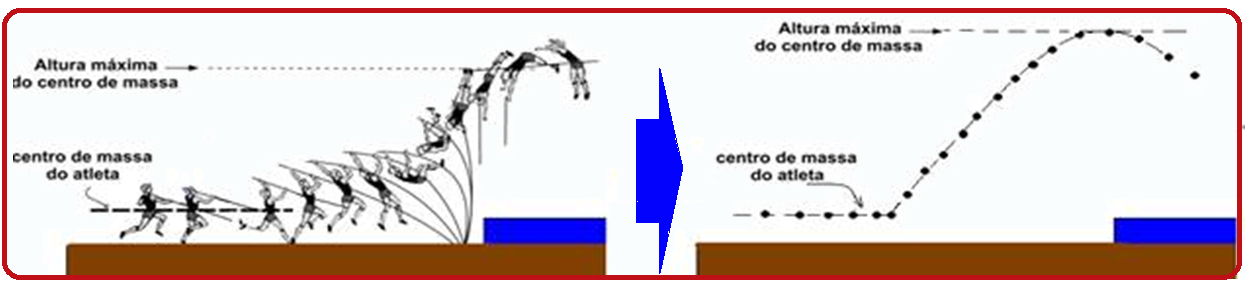
um lançamento oblíquo (trajetória parabólica).

“ A quantidade de movimento de um corpo (ou de um sistema de corpos) é igual à quantidade de movimento do centro de massa desse corpo ou desse sistema de corpos”

Em qualquer tipo de colisão, quem se conserva sempre é a quantidade de movimento e não, necessariamente a energia mecânica.

Colisão Oblíqua

Exercícios de vestibulares com resolução comentada sobre

Conservação da Quantidade de Movimento

01-(PUC-RS) Um sistema é constituído de duas esferas que se movem sobre um plano horizontal e colidem entre si num determinado instante. Imediatamente após a colisão, pode-se afirmar que, referente ao sistema, permaneceu inalterada a

a) energia cinética.

b) energia elástica.

c) quantidade de movimento.

d)velocidade.

e)energia mecânica.

02-(UFV-MG) Um trenó, com massa total de 250kg, desliza no gelo à velocidade de 10 m/s. Se o o seu condutor atirar para trás

50 kg de carga à velocidade de 10m/s, a nova velocidade do trenó será de:

03-(Ufsc-PE) Dois astronautas, A e B, encontram-se livres na parte externa de uma estação espacial, sendo desprezíveis as forças de atração gravitacional sobre eles. Os astronautas com seus trajes espaciais têm massas m_A = 100 kg e m_B = 90 kg, além de um tanque de oxigênio transportado pelo astronauta A, de massa 10 kg. Ambos estão em repouso em relação à estação espacial, quando o astronauta A lança o tanque de oxigênio para o astronauta B com uma velocidade de 5,0 m/s. O tanque choca-se com o astronauta B que o agarra, mantendo-o junto a si, enquanto se afasta.

Considerando como referencial a estação espacial, assinale a(s) proposição(ões) CORRETA(S) e anote sua soma:

(01) Considerando que a resultante das forças externas é nula, podemos afirmar que a quantidade de movimento total do sistema constituído pelos dois astronautas e o tanque se conserva.

(02) Como é válida a terceira lei de Newton, o astronauta A, imediatamente após lançar o tanque para o astronauta B, afasta-se com velocidade igual a 5,0 m/s.

(04) Antes de o tanque ter sido lançado, a quantidade de movimento total do sistema constituído pelos dois astronautas e o tanque era nula.

(08) Após o tanque ter sido lançado, a quantidade de movimento do sistema constituído pelos dois astronautas e o tanque permanece nula.

(16) Imediatamente após agarrar o tanque, o astronauta B passa a deslocar-se com velocidade de módulo igual a 0,5 m/s.

04-(Ufjf-MG) Um asteróide aproxima-se perigosamente da Terra ameaçando destruí-la. Sua massa é de 10 toneladas e sua velocidade de aproximação, em relação à Terra, é de 100 km/h. Super-Homem é então convocado para salvar o planeta.

Sendo sua massa de 50 kg, qual a velocidade, em relação à Terra, com que ele deve atingir frontalmente o asteróide para que os dois fiquem parados, em relação à Terra, após a colisão (despreze a atração gravitacional da Terra)?

a) 20000 km/h;

b) 500 km/h;

c) 250 km/h;

d) 80 km/h.

e) 12.000 km/h

05-(Uem) Um vagão, deslocando-se para a direita com uma velocidade de 10 m/s, é fragmentado por uma explosão, em dois pedaços (1) e (2) de massas iguais, conforme mostra a figura a seguir.

Sejam e ‚ as velocidades respectivas dos dois fragmentos logo após a explosão e considerando que e ‚ possuem a mesma direção do movimento inicial, assinale, dentre as alternativas a seguir, aquela(s) que poderia(m) corresponder ao(s) movimento(s) de (1) e (2) depois da explosão. Anote a soma das verdadeiras:

(01) v₂ = 15 m/s para a direita e v₁ = 5 m/s para a esquerda.

(02) v₂ = 20 m/s para a direita e v₁ = 0.

(04) v₂ = 30 m/s para a direita e v₁ = 10 m/s para a esquerda.

(08) v₂ = 25 m/s para a direita e v₁ = 0.

(16) v₂ = 25 m/s para a direita e v₁ = 5 m/s para a esquerda.

(32) v₂ = 10 m/s para a direita e v₁ = 0.

(64) v₂ = 50 m/s para a direita e v₁ = 30 m/s para a esquerda.

06-(Ufpe) Um casal de patinadores pesando 80 kg e 60 kg, parados um de frente para o outro, empurram-se bruscamente de modo a se movimentarem em sentidos opostos sobre uma superfície horizontal sem atrito.

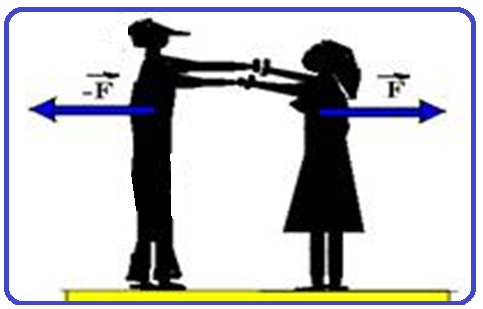
Num determinado instante, o patinador mais pesado encontra-se a 12 m do ponto onde os dois se empurraram. Calcule a distância, em metros, que separa os dois patinadores neste instante.

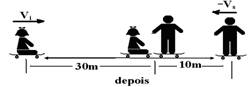
07-(Ufu-MG) Um skatista, sabendo que sua massa é de 45 kg, deseja saber a massa de sua irmãzinha menor. Sendo ele um bom conhecedor das leis da Física, realiza o seguinte experimento: ele fica sobre um skate e coloca sua irmãzinha sentada em outro skate, distante 40 m de sua posição, conforme figura a seguir.

Uma corda muito leve é amarrada no skate da irmãzinha e o skatista exerce um puxão na corda, trazendo o skate e a irmãzinha em sua direção, de forma que ambos se encontram a 10 m da posição inicial do skatista.

Sabendo-se que cada skate possui massa de 1 kg e, desprezando o peso da corda e o atrito das rodas dos skates com o chão, após alguns cálculos o skatista conclui que a massa de sua irmãzinha é de

08-(Ufrrj-RJ)

FIM DA 2^a GUERRA MUNDIAL - BOMBA ATÔMICA

SESSENTA ANOS DE TERROR NUCLEAR

Destruídas por bombas, Hiroshima e Nagasaki hoje lideram luta contra essas armas

Domingo, 31 de julho de 2005 - "O GLOBO"

Gilberto Scofield Jr.

Enviado especial Hiroshima, Japão

"Shizuko Abe tinha 18 anos no dia 6 de agosto de 1945 e, como todos os jovens japoneses durante a Segunda Guerra Mundial, ela havia abandonado os estudos para se dedicar ao esforço de guerra. Era um dia claro e quente de verão e às 8h, Shizuko e seus colegas iniciavam a derrubada de parte das casas de madeira do centro de Hiroshima para tentar criar um cordão de isolamento antiincêndio no caso de um bombardeio incendiário aéreo. Àquela altura, ninguém imaginava que Hiroshima seria o laboratório de outro tipo de bombardeio, muito mais devastador e letal, para o qual os abrigos antiincêndio foram inúteis".

"Hiroshima, Japão. Passear pelas ruas de Hiroshima hoje - 60 anos depois da tragédia que matou 140 mil pessoas e deixou cicatrizes eternas em outros 60 mil, numa população de 400 mil - é nunca esquecer o passado. Apesar de rica e moderna com seus 1,1 milhão de habitantes circulando em bem cuidadas ruas e avenidas, os monumentos às vítimas do terror atômico estão em todos os lugares".

Um exemplo de processo nuclear que pode ocorrer na Natureza é aquele em que alguns núcleos atômicos espontaneamente se desintegram, produzindo um outro núcleo mais leve e uma partícula chamada partícula a. Consideremos, então, um modelo representativo desse processo, formado por uma certa partícula, inicialmente em repouso, que explode, resultando em duas outras partículas, 1 e 2, de massas M₁ = 234g e M₂ = 4g.

Supondo que após a explosão, a partícula 1 saia com uma velocidade de 1,0 . 10² m/s,

a) determine a velocidade com que sai a partícula 2, supondo que ela seja freada até o repouso

b) calcule o trabalho realizado para freá-la;

c) calcule a intensidade da força necessária para fazer parar a partícula 2 em uma distância de 10m, supondo esta força constante.

09-(FUVEST-SP) Num espetáculo de fogos de artifício, um rojão, de massa M_o = 0,5 kg, após seu lançamento, descreve no céu a trajetória indicada na figura. No ponto mais alto de sua trajetória (ponto P), o rojão explode, dividindo-se em dois fragmentos, A e B, de massas iguais a M_o/2. Logo após a explosão, a velocidade horizontal de A, V_A, é nula, bem como sua velocidade vertical.

NOTE E ADOTE:

A massa do explosivo pode ser considerada desprezível.

a) Determine o intervalo de tempo T_o, em segundos, transcorrido entre o lançamento do rojão e a explosão no ponto P.

b) Determine a velocidade horizontal V_B, do fragmento B, logo após a explosão, em m/s.

c) Considerando apenas o que ocorre no momento da explosão, determine a energia E₀fornecida pelo explosivo aos dois fragmentos A e B, em joules.

10-(Ufjf-MG) Um avião bombardeiro, voando em linha reta com uma velocidade V na horizontal, solta uma bomba que se fragmenta em duas partes em algum instante antes de tocar o solo. Sabendo-se que a massa total da bomba é M e que um dos fragmentos fica com massa (1/3)M e a outra (2/3)M, se os fragmentos tocam o solo simultaneamente, qual a razão entre as distâncias horizontais do fragmento menor e do fragmento maior, quando as mesmas tocam o solo, em relação à posição do avião na direção horizontal? Despreze a resistência do ar e considere que a topografia do local seja totalmente plana.

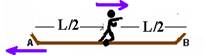
11-(Ufrj-RJ) A figura a seguir representa, uma jangada de comprimento L, em repouso, flutuando em alto mar com o pescador de pé, equidistante das extremidades. Por inadvertência, ele havia levado a jangada para um local onde a Marinha de Guerra estava realizando exercícios de tiro. Assim, em determinado instante, ele percebe um torpedo que se desloca numa direção perpendicular à do comprimento da jangada e que irá atingi-la muito próximo de uma de suas extremidades.

Para tentar evitar que a jangada seja atingida, o pescador deve correr ao longo da direção AB, aproximando-se de A ou de B? Justifique sua resposta.

12-(UNIFESP-SP) Um pescador está em um barco em repouso em um lago de águas tranqüilas. A massa do pescador é de 70 kg; a massa do barco e demais equipamentos nele contidos é de 180 kg.

a) Suponha que o pescador esteja em pé e dê um passo para a proa (dianteira do barco). O que acontece com o barco? Justifique.

(Desconsidere possíveis movimentos oscilatórios e o atrito viscoso entre o barco e a água.)

b) Em um determinado instante, com o barco em repouso em relação à água, o pescador resolve deslocar seu barco para frente com uma única remada. Suponha que o módulo da força média exercida pelos remos sobre a água, para trás, seja de 250 N e o intervalo de tempo em que os remos interagem com a água seja de 2,0 segundos.

Admitindo desprezível o atrito entre o barco e a água, qual a velocidade do barco em relação à água ao final desses 2,0 s?

13-(UFSC) Na situação apresentada na figura a seguir desconsidere o efeito do atrito.

Estando todas as partes em repouso no início, uma pessoa puxa com sua mão uma corda que está amarrada ao outro barco. Considere que o barco vazio (B) tenha a metade da massa do barco mais a pessoa que formam o conjunto (A).

Assinale a(s) proposição(ões) CORRETA(S) e anote sua soma.

(01) Após a pessoa puxar a corda, ambos os barcos se moverão com a mesma velocidade.

(02) Após o puxar da corda, o módulo da velocidade de B será o dobro do módulo da velocidade de A.

(04) É impossível fazer qualquer afirmação sobre as velocidades das partes do sistema ao se iniciar o movimento.

(08) Após o puxar da corda, as quantidades de movimento dos barcos apresentarão dependência entre si.

(16) Ao se iniciar o movimento, a energia cinética de A é sempre igual à energia cinética de B.

14-(Ufu-MG) Um garoto brinca com seu barquinho de papel, que tem uma massa igual a 30 g e está navegando sobre um pequeno lago. Em certo instante, ele coloca sobre o barquinho, sem tocá-lo, uma bolinha de isopor e percebe que o barquinho passa a andar com metade de sua velocidade inicial. Seu irmão mais velho, que observa a brincadeira, resolve estimar a massa da bolinha de isopor com base na variação da velocidade do barquinho. Desprezando efeitos relativos ao empuxo, ele conclui que a massa da bolinha é de

15- (Ufu-MG) João, em um ato de gentileza, empurra uma poltrona para Maria, que a espera em repouso num segundo plano horizontal (0,8 m abaixo do plano de João). A poltrona tem uma massa de 10 kg e Maria tem uma massa de 50 kg. O chão é tão liso que todos os atritos podem ser desprezados, conforme figura 1.

A poltrona é empurrada de A até B, partindo do repouso em A. João exerce uma força constante igual a 25 N, na direção horizontal. Em B a poltrona é solta, descendo a pequena rampa de 0,8 m de altura. Quando a poltrona chega com uma certa velocidade (v) em Maria, ela senta-se rapidamente na poltrona, sem exercer qualquer força horizontal sobre ela, e o sistema poltrona + Maria escorrega no segundo plano horizontal, conforme figura 2.

Considerando a aceleração da gravidade como 10 m/s², calcule:

a) o trabalho realizado por João no percurso AB.

b) a velocidade (v) da poltrona ao chegar em Maria.

c) a velocidade do sistema poltrona + Maria, após Maria sentar-se na poltrona.

16-(PUC-SP) Um tronco de massa 50kg desce um rio levado pela correnteza com velocidade constante de 2,0m/s. Uma ave de massa 10kg, voando a 2,0m/s, rio acima, procura pousar sobre o tronco. A ave escorrega de uma extremidade a outra sem conseguir permanecer sobre o tronco, saindo com velocidade de 0,5m/s. Desprezando a resistência da água, qual a velocidade do tronco, assim que a ave o abandona?

17-(Ufjf-MG) Quando se abre uma torneira de forma que saia apenas um "filete" de água, a área da seção reta do filete de água

abaixo da boca da torneira é tanto menor quanto mais distante dela, porque:

a) como a velocidade da água distante da boca da torneira é maior devido à ação da força gravitacional, para que haja conservação da massa, a área da seção reta do filete tem que ser menor.

b) uma vez que a velocidade da água distante da boca da torneira é menor devido à ação da força gravitacional, para que haja conservação da massa, a área da seção reta do filete tem que ser menor.

c) a velocidade da água caindo não depende da força gravitacional e, portanto, para que haja conservação da massa, a área da seção reta do filete tem que ser menor.

d) as interações entre as moléculas da água tornam-se mais intensas devido à ação da força gravitacional e, assim, a área da seção reta do filete distante da boca da torneira fica menor.

e) devido à velocidade com que a água sai, a boca da torneira é projetada para que a água seja concentrada mais distante da boca.

18-(ITA-SP) Todo caçador, ao atirar com um rifle, mantém a arma firmemente apertada contra o ombro evitando assim o "coice" da mesma. Considere que a massa do atirador é 95,0 kg, a massa do rifle é 5,00 kg e a massa do projétil é 15,0 g a qual é disparada a uma velocidade de 3,00 × 10² m/s. Nestas condições, determine a velocidade de recuo do rifle (Vr) quando se segura muito frouxamente a arma e a velocidade de recuo do atirador (Va) quando ele mantém a arma firmemente apoiada no ombro.

19- (UNICAMP-SP) Imagine a seguinte situação: um dálmata corre e pula para dentro de um pequeno trenó, até então parado, caindo nos braços de sua dona. Em consequência, o trenó começa a se movimentar.

Considere os seguintes dados:

I. a massa do cachorro é de 10kg;

II. a massa do conjunto trenó + moça é de 90kg;

III. a velocidade horizontal do cachorro imediatamente antes de ser seguro por sua dona é de 18km/h.

a) Desprezando-se o atrito entre o trenó e o gelo, determine a velocidade horizontal do sistema trenó + moça + cachorro, imediatamente após o cachorro ter caído nos braços de sua dona.

b) Determine a variação de energia cinética no processo.

20-(UnB-DF) Aprende-se em aulas de educação física que, ao se saltar, é fundamental flexionar as pernas para amenizar o impacto no solo e evitar danos à coluna vertebral, que possui certo grau de flexibilidade. No caso de uma queda em pé, com as pernas esticadas, uma pessoa pode chegar a ter, no estado de maior compressão da coluna, a sua altura diminuída em até 3 cm. Nesse caso, o esqueleto da pessoa, com a velocidade adquirida durante a queda, desacelera bruscamente no espaço máximo de 3 cm. Supondo que uma pessoa de 70 kg caia de um degrau de 0,5 m de altura, atingindo o solo em pé, com as pernas esticadas e recebendo todo o impacto diretamente sobre o calcanhar e a coluna, julgue os itens seguintes.

(1) No instante em que a pessoa deixa o degrau, a variação do seu momento linear é produzida pela força peso.

(2) Durante o impacto, a força de compressão média a que a coluna está sujeita é momentaneamente superior ao peso correspondente à massa de 1 tonelada.

(3) Em módulo, a força de compressão da coluna é igual à força que o solo exerce nos pés da pessoa.

(4) Se flexionasse as pernas, a pessoa aumentaria o espaço de desaceleração, diminuindo, portanto, o impacto do choque com o solo.

21-(FUVEST-SP) Um objeto A de massa M=4,0kg, é largado da janela de um edifício, de uma altura H_o=45m. Procurando diminuir o impacto de A com o chão, um objeto B, de mesma massa, é lançado um pouco depois, a partir do chão, verticalmente, com velocidade inicial V_oB. Os dois objetos colidem a uma altura de 25m, com velocidades de mesmo módulo. Com o impacto, grudam-se ambos, um no outro, formando um só corpo AB, de massa 2M, que cai atingindo o chão.

a) Determine a energia mecânica Q, em joules, dissipada na colisão.

b) Determine a energia cinética Ec, em joules, imediatamente antes de AB atingir o solo.

22-(UnB-DF) Novos sistemas de propulsão de foguetes e de sondas espaciais estão sempre sendo estudados pela Nasa. Um dos projetos utiliza o princípio de atirar e receber bolas de metal para ganhar impulso. O sistema funcionaria da seguinte forma: em uma estação espacial, um disco girando, atiraria bolas metálicas a uma velocidade de 7.200km/h. Uma sonda espacial as receberia e as mandaria de volta ao disco da estação. Segundo pesquisadores esse sistema de receber e atirar bolas de metal poderia ser usado para dar o impulso inicial a naves ou sondas espaciais que já estivessem em órbita. (Folha de São Paulo,13/12/1988:com adaptações)

Considere uma sonda espacial com massa de 1 tonelada, em repouso em relação a uma estação espacial, conforme a figura acima.

Suponha que a sonda receba, pela entrada E, uma bola de 10kg, atirada a 2.000m/s pelo disco da estação e a devolva, pela saída S, com um quinto do módulo da velocidade inicial. Calcule, em m/s, o módulo da velocidade da sonda em relação à estação no instante em que a bola é devolvida. Despreze a parte fracionária do resultado, caso exista.

23-(FUVEST-SP) Um asteróide, no espaço, está em repouso em relação a um determinado referencial. Num certo instante ele explode em três fragmentos. Dentre os esquemas representados, assinale o único que pode representar os vetores velocidades dos fragmentos do asteróide logo após a explosão, em relação ao referencial inicial.

24-(UFSCAR-SP) Uma granada está em repouso sobre um plano horizontal sem atrito. Ela explode em três pedaços de massas m₁, m₂ e m₃. Após a explosão, que se deu no ponto D, o pedaço de massa m₁ se movimenta na direção e sentido do eixo X com velocidade , enquanto o pedaço de massa m₂ se movimenta com velocidade na direção e sentido do eixo Y.

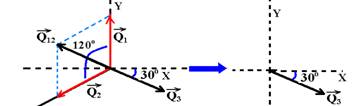
Sabendo que m₁=m₂ e que V₁=V₂, qual das setas pode indicar a direção e o sentido do movimento de m₃ imediatamente após a explosão?

25-(Ufpb) Há 60 anos, lamentavelmente, foi lançada, sobre Hiroshima, uma bomba atômica cujo princípio físico é o da fissão nuclear. Nesse processo, um núcleo atômico pesado divide-se em núcleos menores, liberando grande quantidade de energia em todas as direções. Suponha que o núcleo de um determinado átomo parte-se em três pedaços de mesma massa, movendo-se com velocidades iguais em módulo (v₁ = v₂ = v₃ = v), nas direções indicadas na figura.

Considere a massa total, após a divisão, igual à massa inicial.

A velocidade v_i do núcleo, antes da divisão, é:

26- (PUC-PR) Uma granada é lançada verticalmente com uma velocidade V_o. Decorrido um tempo, sua velocidade é V_o/2 para cima, quando ocorre a explosão. A granada fragmenta-se em quatro pedaços, de mesma massa, cujas velocidades imediatamente após a explosão são apresentadas na figura.

Considerando a conservação da quantidade de movimento, e, dentre as alternativas possíveis que relacionam o módulo da velocidade, assinale a única correta:

27-(INATEL-MG) Uma explosão divide um pedaço de rocha em três partes de massas m₁=m₂=20kg e m₃=40kg. As partes m₁ e m₂ são lançadas a uma velocidade de 20m/s, conforme as orientações indicadas na figura abaixo.

Considerando o sistema isolado de forças externas, calcula-se que o módulo da velocidade da parte m₃é V₃=10m/s, com a seguinte orientação:

28-(UNICAMP-SP) A existência do neutrino e do antineutrino foi proposta em 1930 por Wolfang Pauli, que aplicou as leis da conservação de quantidade de movimento e energia ao processo de desintegração b. O esquema abaixo ilustra esse processo para um núcleo de trítio, H³, (um isótopo do hidrogênio), que se transforma em um núcleo de hélio, He³, mais um eletron e ^-, e um antineutrino, . O núcleo de trítio encontra-se inicialmente em repouso. Após a desintegração, o núcleo de Hélio possui uma quantidade de movimento com módulo de 12.10^-24kg.m/s e o elétron sai em uma trajetória fazendo um ângulo de 60^ocom o eixo horizontal e uma quantidade de movimento de módulo 6,0.10^-24kg.m/s.

a) O ângulo a que a trajetória do neutrino faz com o eixo horizontal é de 30^o. Determine o módulo da quantidade de movimento do antineutrino.

b) Qual é a velocidade do núcleo de hélio pós a desintegração? A massa do núcleo de hélio é 5,0.

10^-27kg.

29-(UNICAMP-SP) Uma bomba explode em três fragmentos na forma mostrada na figura a seguir.

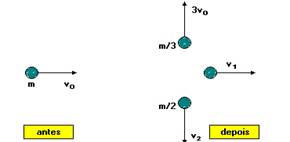
a) Ache v₂ em termos de v_o.

b) Ache v₁ em termos de v_o.

c) A energia mecânica aumenta, diminui ou permanece a mesma? Justifique.

30-(FUVEST-SP) Um corpo de 6,0 kg, deslocando-se com velocidade na direção e sentido de um eixo x e livre de forças externas, explode, separando-se em dois pedaços, A e B, de massas mA e mB, respectivamente. Após a explosão, A e B passam a se deslocar no plano xOy, afastando-se do ponto O com velocidades e , respectivamente, segundo as direções representadas esquematicamente por linhas pontilhadas na figura

a) Sendo v o módulo de e sabendo que os módulos das componentes vetoriais de e na direção de x valem, respectivamente, V/2 e 2V, determine as massas m_A e m_B.

b) Sendo V_AY e V_BY, respectivamente, os módulos das componentes de e na direção de y, determine a razão V_A/V_B.

31-(UNICAMP-SP) O lixo espacial é composto por partes de naves espaciais e satélites fora de operação abandonados em órbita ao redor da Terra. Esses objetos podem colidir com satélites, além de pôr em risco astronautas em atividades extraveiculares. Considere que durante um reparo na estação espacial, um astronauta substitui um painel solar, de massa m_p = 80

kg, cuja estrutura foi danificada. O astronauta estava inicialmente em repouso em relação à estação e ao abandonar o painel no espaço, lança-o com uma velocidade v_p = 0,15 m/s.

a) Sabendo que a massa do astronauta é m_a = 60 kg, calcule sua velocidade de recuo.

b) O gráfico a seguir mostra, de forma simplificada, o módulo da força aplicada pelo astronauta sobre o painel em função do

tempo durante o lançamento. Sabendo que a variação de momento linear é igual ao impulso, cujo módulo pode ser obtido pela área do gráfico, calcule a força máxima F_max.

32-(UFSC-SC) Dois patinadores, um homem e um menino, de massas respectivamente iguais a 60 kg e 30 kg, estão em pé, de frente um para o outro, em repouso, sobre uma superfície de gelo, lisa, plana e horizontal. Quando um empurra o outro, o homem adquire uma velocidade de 0,3 m/s em relação ao gelo.

Considerando desprezível o atrito entre os patins dos patinadores e o gelo, assinale a(s) proposição(ões) CORRETA(S).

01) A distância entre os patinadores 2,0 s após eles se separarem é de 1,8 m.

02) A energia mecânica do sistema homem-menino se conserva.

04) As forças que o homem e o menino fazem um sobre o outro são conservativas.

08) A força externa resultante sobre o sistema homem-menino é nula.

16) Como a massa do homem é maior do que a do menino, a quantidade de movimento do sistema tem o mesmo sentido que a quantidade de movimento do homem.

32) As forças internas que atuam no sistema homem-menino não alteram a quantidade de movimento total do sistema.

33-(FUVEST-SP) A partícula neutra conhecida como méson K_o é instável e decai, emitindo duas partículas, com massas iguais, uma positiva e outra negativa, chamadas, respectivamente, méson e méson . Em um experimento, foi observado o

decaimento de um K_o, em repouso, com emissão do par e . Das figuras a seguir, qual poderia representar as direções e sentidos das velocidades das partículas e no sistema de referência em que o K_o estava em repouso?

34-(ITA-SP) Uma massa m₁ com velocidade inicial V_o colide com um sistema massa-mola m₂ e constante elástica k, inicialmente em repouso sobre uma superfície sem atrito, conforme ilustra a figura.

Determine o máximo comprimento de compressão da mola, considerando desprezível a sua massa.

35-(UFG-GO) Um arqueiro está posicionado a determinada distância do ponto P, de onde um alvo é lançado do solo verticalmente e alcança a altura máxima H = 20 m. Flechas são lançadas de uma altura igual a h_o = 2,0 m com velocidade de módulo de 21 m/s. Em uma de suas tentativas, o arqueiro acerta o alvo no instante em que tanto a flecha quanto o alvo encontram-se na posição mais alta de suas trajetórias, conforme ilustra a figura.

Sabendo que a massa do alvo é cinco vezes a da flecha e desprezando as perdas de energia por atrito, calcule:

a) a velocidade do conjunto flecha-alvo imediatamente após a colisão;

b) a distância L, considerando o fato de que a flecha e o alvo chegam solidários ao solo.

36-(PUC-RS) Em uma rodoviária, um funcionário joga uma mala de 20,0 kg com velocidade

horizontal de 4,00 m/s, sobre um carrinho de 60,0 kg, que estava parado. O carrinho pode mover-se livremente sem atrito; além disso, a resistência do ar é desprezada. Considerando que a mala escorrega sobre o carrinho e para, é correto afirmar que, nessa colisão entre a mala e o carrinho, o módulo da velocidade horizontal adquirida pelo sistema carrinho-mala é ____________ e a energia mecânica do sistema __________________.

As expressões que completam correta e respectivamente as lacunas são:

a) 1,33m/s; permanece a mesma

b) 1,33m/s; diminui

c) 1,00m/s; diminui

d) 1,00m/s; aumenta

e) 4,00m/s; permanece a mesma

37-(FUVEST-SP) Um gavião avista, abaixo dele, um melro e, para apanhá-lo, passa a voar

verticalmente, conseguindo agarrá-lo. Imediatamente antes do instante em que o gavião, de massa M_G = 300 g, agarra o melro, de massa M_M = 100 g, as velocidades do gavião e do melro são, respectivamente, V_G = 80 km/h na direção vertical, para baixo, e V_M = 24 km/h na direção horizontal, para a direita, como ilustra a figura acima. Imediatamente após a caça, o vetor velocidade u do gavião, que voa segurando o melro, forma um ângulo α com o plano horizontal tal que tg α é aproximadamente igual a

38-(UNICAMP-SP)

O tempo de viagem de qualquer entrada da Unicamp até a região central do campus é de apenas alguns minutos.

Assim, a economia de tempo obtida, desrespeitando-se o limite de velocidade, é muito pequena, enquanto o risco de acidentes aumenta significativamente.

a) Considere que um ônibus de massa M = 9000 kg , viajando a 80 km/h, colide na traseira de um carro de massa m_a=1000 kg

que se encontrava parado. A colisão é inelástica, ou seja, carro e ônibus seguem grudados após a batida. Calcule a velocidade do

conjunto logo após a colisão.

b) Além do excesso de velocidade, a falta de manutenção do veículo pode causar acidentes. Por exemplo, o desalinhamento das rodas faz com que o carro sofra a ação de uma força lateral. Considere um carro com um pneu dianteiro desalinhado de 3°,

conforme a figura abaixo, gerando uma componente lateral da força de atrito em uma das rodas.

Para um carro de massa m_b=1600 kg, calcule o módulo da aceleração lateral do carro, sabendo que o módulo da força de atrito em cada roda vale F_at= 8000 N . Dados:sen 3° = 0,05 e cos 3° = 0,99.

Resolução comentada dos exercícios de vestibulares sobre

Conservação da Quantidade de Movimento

01- R- C (veja teoria)

02- Q_a=mV=(250 ).10 --- Q_a=2.500kg.m/s --- Q_d=m_c.V_c + m_t.V_t=50.(-10) + 200.(+V_t) --- Q_d= - 500 + 200.V_t --- Q_a=Q_d --- 2.500= - 500 +200.V_t --- V_t=15m/s R- E

03- (01) verdadeira (veja teoria) --- (02) falsa – sua massa é diferente da massa do tanque --- (04) verdadeira - (ambos estavam parados) --- (08) falsa – ambos possuem velocidades de sentidos contrários --- (16) antes do choque do tanque com o astronauta B – Q_a=m_t.V_t + m_B.V_B --- 10.5 + 90X0 --- Q_a=50kg.m/s --- após o choque, astronauta + tanque (m=90 + 10=100kg) tem velocidade comum V --- Q_d=100.V --- Q_a=Q_d --- 50=100V --- V=0,5m/s(verdadeira)

(01+04+08+16)=29

04- antes --- Q_a=m_a.V_a + m_SH.V_SH =10.000X100 + 50.(-V_SH) --- Q_a=10⁶ – 50V_HS --- depois --- Q_d=m_SH.V_SH + m_a.V_a=0 + 0=0 --- Q_a=Q_d --- 100.10⁴- 50.V_SH --- V_SH=2.10⁴km/h R- A

05- Sendo a velocidade uma grandeza vetorial, vamos orientá-la como, por exemplo, para a direita positiva e para a esquerda, negativa e vamos supor que, após o choque, ambos os fragmentos se movam para a direita --- Q_a (antes da explosão) --- Q_a=mV=m.10 --- Q_a=10m --- Q_d (depois da explosão) --- Q_d=m/2V₂ + m/2V₁ --- Q_d=(mV₂ + mV₁)/2 --- Q_a = Q_d --- 10m=(mV₂ + mV₁)/2 --- V₂+ V₁=20 --- com a trajetória orientada para a direita, a soma algébrica das duas velocidades deve ser 20.(01) +15 -5=10m/s (falsa) --- (02) +20 + 0=20m/s (verdadeira) --- (04) +30 -10=20m/s (verdadeira) --- (08) +25 + 0=25m/s (falsa) --- (16) +25 – 5=20m/s (verdadeira) --- (32) +10 + 0=10m/s (falsa) --- (64) +50 – 30=20m/s (verdadeira)

Soma (02 + 04 + 16 + 64) = 86

06- Q_a=0 --- Q_d= mv +M(-V)=60.∆s/∆t – 80.∆S/∆t= 60.∆s/∆t – 80.12/∆t --- Q_d= 60.∆s/∆t – 960/∆t --- Q_a=Q_d --- 0=60.∆s/∆t – 960/∆t --- ∆t é o mesmo e se cancela --- 60.∆s=960 --- ∆s=16m --- a distância entre eles é d=12m + 16m --- d=28m

07- Q_a=0 --- Q_d=(45 + 1).(-V_s) + (m + 1).V_i= - 46V_s + (m + 1)V_i= - 46.10/∆t + (m + 1).30/∆t --- Q_d=( - 460 +

30m + 30)/ ∆t ---Q_a=Q_d --- 0==( - 460 + 30m + 30)/ ∆t --- 30m – 430=0 --- m=14,33kg R- D

08- a) Q_a=0 --- Q_d=M₁.V₁ + M₂.V₂=234.10^-3.1,0.10² + 4.10^-3.V₂ --- Q_d=234.10^-1 – 4.10^-3.V₂ --- Q_a=Q_d --- 0=234.10^-1 – 4.10^-3.V₂ --- V₂=5,85.10³m/s

b) a variação da energia cinética da partícula fornece o trabalho necessário para pará-la --- E_ca=0 --- E_cd=234.10^-3(1,0.10²)²/2 +4.10^-3.(5,85.10³)²/2 --- W=E_cd – E_ca= - 6,8.10⁴J

c) W=F.d.cos0^o --- 6,8.10⁴=F.10 --- F=6,8.10³N

09- a) cálculo da componente vertical (V_oy) da velocidade inicial V_o --- na altura máxima (h=45m) – V_y=0 --- Vy² = V_oy² + 2.(-g).h --- 0²=V_oy² – 2.10.45 --- V_oy=30m/s --- tempo para atingir a altura máxima --- V_y=V_oy –gt --- 0=30 – 10.t --- t=T_o=3s

b) para atingir a altura máxima ele percorreu uma distância horizontal x=60m em t=3s --- x=x_o + V_x.t --- 60=0 + V_x.3 --- V_x=20m/s

c) no ponto mais alto da trajetória o rojão, antes de explodir, tem apenas velocidade horizontal V_x=20m/s e sua quantidade de movimento vale Q_a=mV=0,5.20 --- Q_a=10kg.m/s (horizontal e para a direita) --- após a explosão, as componentes horizontal e vertical do fragmento A são nulas, sobrando apenas a componente horizontal do fragmento B, que também deve ser horizontal e para a direita, pois, Q_a=Q_d --- Q_d=0,25.V --- 10=0,25.V --- V=40m/s (componente horizontal da velocidade do fragmento B) --- a energia fornecida pelo combustível corresponde à variação de energia cinética antes e depois da explosão, tomando este ponto como nível zero de altura (E_p=0) --- E_ca=mV²/2 =0,5.400/2 --- E_ca=100J --- E_cd=0,25.1600/2=200J --- DE_c=200 – 100=100J

10- Sendo a massa do maior o dobro da massa do menor, a velocidade do menor (V₁) deverá ser o dobro da velocidade do maior (V₂), pelo princípio da conservação da quantidade de movimento --- V₁=2V₂) --- ∆S₁/∆t=2∆S₂/∆t --- sendo ∆t o mesmo --- ∆S₁=2∆S₂ --- ∆S₁/∆S₂=2 R- C

11- O pescador deve correr para B, a fim de que a força que seus pés exercem sobre a jangada a

acelere no sentido B para A, fazendo com que ela se afaste da trajetória do torpedo.

12- a) Pela 3.a lei de Newton, ou princípio fundamental da ação e reação o barco irá para trás.

b) F.∆t=m∆V --- 250.2=(180 + 70).(V – 0) --- V=2,0m/s

13-(01) Falsa – massas diferentes, velocidades diferentes.

02-Verdadeira – verdadeira, pois a massa de A é o dobro da massa de B

(04) Falsa

(08) Correta – a quantidade de movimento do sistema antes de puxar a corda é igual à quantidade de movimento do sistema após o puxão.

(16) Falsa – vide teoria

Soma – (02 + 08) = 10

14- O sistema deverá conservar a quantidade de movimento horizontal inicial. Desta forma como a velocidade foi reduzida à metade, a massa do sistema deverá dobrar, passando de 30 g para 60 g. A diferença de 30 g corresponde a massa da bolinha de isopor. R- D

15- a) W=F.d.cosa=25.4.cos0^o --- W=100J

b) velocidade com que a poltrona chega em B --- F=ma --- 25=10.a --- a=2,5m/s² --- V_B²=V_o² + 2.a.DS --- V_B²=0² + 2.2,5.4 --- V_B=√20m/s --- velocidade com que a poltrona chega à Maria (V_M) – conservação da energia mecânica – E_mB=m.V_B²/2 + mgh=10.(√20)²/2 + 10.10.0,8 --- E_mB
=180J --- E_mM=m.V_M²/2 + m.g.h=10.V_M²/2 + 0 --- E_mM=5V_M² --- 180=5V_M² --- V_M=6m/s

c) conservação da quantidade de movimento – antes de Maria sentar na poltrona – Q_a=m.V=10.6 --- Q_A=60kg.m/s --- depois que Maria sentou, o sistema Maria + poltrona movem-se juntos com velocidade V --- Q_d=60.V --- Q_a=Q_d--- 60=60V --- V=1m/s

16- Q_a=50.(+2) + 10.(-2)=80kg.m/s --- Q_d=50.(V) + 10.(-0,5)=50V – 5 --- Q_a=Q_d --- 80=50V – 5 --- V=1,7m/s R- D

17- R- A (veja teoria)

18- Velocidade de recuo do rifle --- Q_a=0 --- Q_d=15.10^-3.(+3.10²) + 5.(-V) --- Q_d=45.10^-1 – 5V --- Q_a=Q_d --- 0=45.10^-1 – 5V --- V=0,9m/s --- velocidade de recuo do atirador --- Q_a=0 --- Q_d=15.10^-3.(+3.10²) + (95 +5).(-V)=45.10^-1 – 100V --- Q_a=Q_d --- 0=45.10^-1/100V --- V=4,5.10^-2m/s

19- a) Q_a=M_c.V_c=10.5=50kg.m/s --- Q_d=(90 + 10).V=100V --- Q_d=Q_a --- 50=100V --- V=0,5m/s

b) E_ca=10.25/2=125J --- E_cd=100.0,25/2=12,5J --- ∆E_c=E_cd – E_ca= 12,5 – 125 ---∆E_c=-125J

20-(1) Verdadeira – desprezando-se os atritos ele está em queda livre sob ação exclusiva da força peso.

(2) Velocidade com que ele chega ao solo – V²=V_o² + 2g.h --- V²= 0² + 2.10.0,5 --- V=√10m/s --- módulo da aceleração durante o choque --- V²=V_o² + 2.a. DS --- 0²=(√10)² -2.a.0,03 --- a=333m/s² --- F=ma=70.333,3 --- F=23.310N (força que ele troca com o solo) que é maior que o peso de 1.000kg (1.000 X 10=10.000N) – Verdadeira

(3) Verdadeira – princípio da ação e reação

(04) Verdadeira – (veja teoria).

Todas verdadeiras

21- a) Objeto A – queda livre com V_oA=0 --- a colisão ocorre na altura de h=(45 – 25)=20m --- V²=Vo² + 2.g.h --- V²= 0² + 2.10.20 --- V=20m/s --- No encontro V_A=V_B=20m/s – antes da colisão Q_a=M(+V_A) + M.(-V_B)=M.(+20) + M.(-20) --- Q_a=0 --- Q_d=2M.V_AB --- Q_a=Q_d -- 2M.V_A=0 --- V_AB=0 --- a energia mecânica dissipada na colisão corresponde a E_mdepois – E_mantes --- DE_m=2M.V_AB – (M.V_A²/2 + M.V_B²/2)= 2.4.0 –(4.20²/2 + 4.(-20)²/2) --- --- DE_m= 0 –(800 + 800) --- DE_m= - 1600J

b) variação de energia mecânica --- E_mA= E_pA + E_cA = mgh + 0= 8.10.25 --- E_mA=2.000J --- E_md=E_cd + E_pd=E_cB+ 0 --- E_mA=E_md
---E_cB=2.000J

22-Orientando a trajetória como positiva no sentido do movimento da sonda (positivo para a esquerda) --- antes – bola chegando à sonda com velocidade de 2.000m/s e a sonda inicialmente parada -- Q_a=m_b.V_b+ m_s.V_s=10.2.000 + 1.000 X 0 --- Q_a=20.000kg.m/s --- depois – bola saindo com velocidade V_b=- 400m/s e a sonda se movendo para a esquerda com velocidade +V --- Q_d=m_b.V_b + m_s.(+V)=10.( - 400) + 1.000V --- Q_d= - 4.000 + 1.000V --- Q_a=Q_d --- 20.000= - 4.000 + 1.000V ---

V=24m/s

23- Como a direção e o sentido da velocidade coincidem com a direção e sentido da quantidade de movimento, e como a quantidade de movimento do sistema antes da explosão é nula, depois da explosão também deverá ser nula. Assim, a única alternativa em que todos os vetores se anulam é a D.

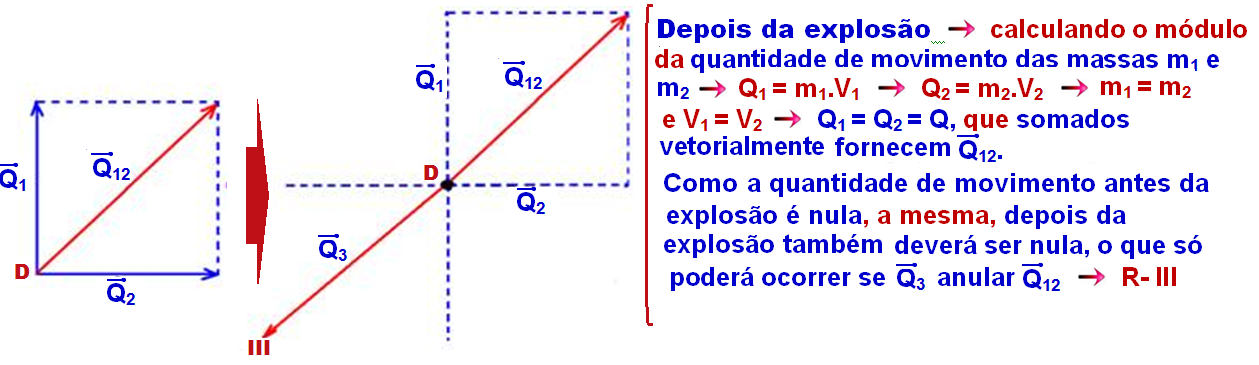
24- Q₁=m₁.V₁ --- Q₂=m₂.V₂ --- m₁=m₂ e V₁=V₂ --- Q₁=Q₂=Q, que somados vetorialmente fornecem Q₁₂

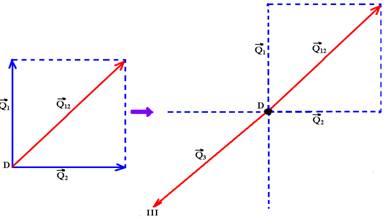
Como a quantidade de movimento antes da explosão é nula, a mesma, depois da explosão também deverá ser nula, o que só poderá ocorrer se anular R- III

25- Multiplicando as velocidades pelas respectivas massas obtemos as quantidades de movimento de cada elemento do sistema antes e depois da fissão

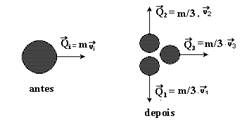
Observe na figura acima que e se anulam, sobrando:

Em módulo --- Q_a=Q_d --- Q_i=Q₃ --- m.v_i=m/3.v₃ --- v_i=v/3 R- E

26- Sendo a quantidade de movimento da granada antes da explosão vertical e para cima, sua quantidade de movimento depois da explosão também deverá ser vertical e para cima e na horizontal deve se anular. R- A

27- Cálculo do módulo de Q₁ e de Q₂ imediatamente depois da explosão --- Q₁=m₁.V₁= 20.20=400kg.m/s --- Q₁= Q₂=400kg.m/s --- somando vetorialmente e obtemos cujo

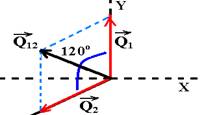
módulo é calculado pela lei dos cossenos --- Q₁₂² = Q₁² + Q₂² + 2Q₁Q₂cos120^o --- Q₁₂²= 400² + 400² + 2.400.400.(-1/2) --- Q₁₂=400kg.m/s --- como a quantidade de movimento antes da explosão é Q_a=0, a quantidade de movimento depois da explosão será também nula (Q_d=0) e, para que isso ocorra deve anular , ou seja, deve ter a mesma intensidade, mesma direção e sentido contrário (figura abaixo

R- D

28- a) Quantidade de movimento do núcleo de trítio antes de se desintegrar --- Q_a=0 (repouso) --- após a desintegração – núcleo do hélio – Q_He³=12.10^-24kg.m/s --- eletron – Q_e^-=6,0.10^-24kg.m/s

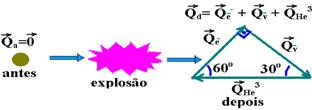
Sen60^o= Q_v/ Q_He³ --- √3/2=Q_v/12.10^-24 --- Q_v=6,0.√3.10^-24kg.m/s

b) Q_He³=m.V --- 12.10^-24=5,0.10^-27.V --- V=2,4.10³m/s

29- Antes --- Q_a=m.v_o

Depois – Q_o=m/3.3v_o=m.v_o – Q₁=m/6.v₁ – Q₂=m/2.v₂

a) Como a quantidade de movimento () antes da explosão é horizontal e para a direita, a quantidade de movimento de movimento () depois da explosão também deverá ser horizontal e para a direita. Assim, e devem se anular, ou seja ---

Q_o=Q₂ --- m.v_o=m/2.v₂ --- v₂=2.v_o

b) Como os vetores verticais se anulam, deve ser igual a , ou seja, --- m.v_o=m/6.v₁ --- v₁=6.v_o

c) Considerando a energia mecânica como sendo apenas a cinética --- antes –E_ma=m.v_o²/2 --- depois --- E_md=m/3.(3v_o)²/2 + m/6.(6v_o)²/2 + m/2.(2v_o)²/2 --- E_md=11m.v_o²/2 --- E_md>E_ma - aumenta

30- a) eixo X --- antes --- Q_a=m.V=6.V --- depois --- Q_d=Q_AX + Q_BX --- Q_d=m_A.V_A+ m_B.V_B --- Q_d=m_A.V/2 + m_B.2V

Q_a=Q_d --- 6.V=m_A.V/2 + m_B.2V --- 12=m_A + 4m_B I --- m_A + m_B=6 --- m_A=6 – m_B II --- II em I --- 12=6 – m_B + 4m_B ---

m_B=2kg --- m_A=4kg

b) na vertical a resultante é nula --- Q_AY=m_A.V_Y=2.V_A --- Q_BY=m_B.V_Y=4.V_B

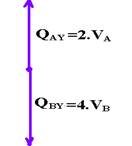
Q_AY=Q_BY
---2V_A=4V_B --- V_A/V_B=2

31- a) Dados --- m_a = 60 kg --- m_p = 80 kg --- v_a = 0,15 m/s --- como se trata de um sistema isolado, há conservação do momento linear (quantidade de movimento) do sistema (Q) --- Q_i=Q_f --- Q_i=0 (inicialmente em repouso) --- Q_f=m_aV_a + m_pV_p --- Q_i=Q_f --- 0= m_aV_a + m_pV_p --- 60.V_a=80.(0,15) --- V_a= -0,2m/s (sinal negativo significa que o astronauta recuou) --- V=0,2m/s

|b) Após o empurrão, o momento linear do painel é --- Q_p = m_p v_p = 80.(0,15) = 12 kg.m/s --- como a força aplicada pelo astronauta é a responsável pela variação da velocidade do painel, temos, pelo teorema do impulso --- I_Fa=Q_p=12kg.m/s ---

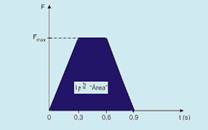
O impulso é numericamente igual à área --- I_Fa=área do trapézio=(B + b).h/2=(0,9 + 0,3).F_max/2 --- I_Fa=0,6F_max --- 12=0,6F_max --- F_max=20N

32- 01) Correta --- trata-se de um sistema mecanicamente isolado (a resultante das forças externas é nula), portanto ocorre conservação da quantidade de movimento ou momento linear --- como a quantidade de movimento inicial do sistema é nula, para ocorrer conservação, o módulo da quantidade de movimento adquirida pelo homem deve ser igual ao módulo da quantidade de movimento adquirida pelo menino --- M_H v_H = M_m v_m --- 60.(0,3) = 30. v_m --- v_m = 0,6 m/s --- a velocidade relativa de afastamento entre eles tem módulo --- v_rel = 0,6 + 0,3 = 0,9 m/s --- então, 2 s após o empurrão, a distância (d) entre eles é:
d = v_rel.Δt = 0,9.(2) --- d = 1,8 m.
02) Falsa --- o sistema é não-conservativo, pois homem e menino consomem energia de seus organismos, trocando forças que realizam trabalho mecânico, transferindo energia cinética ao sistema.
04) Falsa. Forças conservativas transformam energia potencial em cinética ou vice-versa --- no caso há transformação de energia química dos organismos em energia cinética.
08) Correta --- as forças trocadas entre eles têm mesma intensidade, pois formam um par ação-reação --- como são forças internas ao sistema, a resultante dessas forças é nula.

16) Falsa --- veja (01)

32) Correta --- apenas forças externas alteram a quantidade de movimento do sistema, conforme afirma o teorema do impulso --- resultante das forças externas é igual à variação da quantidade de movimento do sistema.

R- (01 + 08 + 32) = 41

33- Trata-se de um sistema mecanicamente isolado, pois apenas forças internas provocam variações de velocidades --- assim, ocorre conservação da quantidade de movimento do sistema --- como se trata de uma grandeza vetorial, as partículas e devem ter velocidades de sentidos e de mesmo módulo, uma vez que as massas são iguais --- essas velocidades também devem se anular, pois como a quantidade de movimento inicial é nula, a final também deverá ser nula --- R- A

34- As variações de velocidades na colisão ocorrem somente pela interação entre a massa m₁ e a massa m₂ formando, então, um sistema mecanicamente isolado --- assim, há conservação da quantidade de movimento do sistema que engloba m₁, m₂ e a mola --- a compressão máxima da mola ocorre quando os dois corpos têm a mesma velocidade

35- a) Dados --- h_o = 2 m --- H = 20 m --- v_o = 21 m/s --- massa da flecha = m --- massa do alvo = 5 m --- conservação da energia mecânica --- cálculo da velocidade com que a flecha atinge o alvo --- E_mi=E_mf --- mV_o²/2 + mgh=mV²/2 + mgH ---

multiplicando por 2 a equação --- v² = 21² + 20(2 –20) --- v²= 81 --- v = 9 m/s --- como a flecha atinge o alvo no ponto mais alto, no momento de impacto a velocidade do alvo é nula --- o sistema pode ser considerado mecanicamente isolado, e a colisão é inelástica --- assim, pela conservação da quantidade de movimento (momento linear), sendo v’ a velocidade final do sistema --- --- mv = (m + 5m)v’ --- v = 6v’ --- 9 = 6v’ --- v’ = 1,5 m/s.

b) Cálculo do tempo de queda (t_q) do sistema --- H=gt_q²/2 --- t_q=√2x20/10 --- t_q=2s --- na direção horizontal você tem um movimento uniforme --- X=V’.t_q=1,5x2 --- X=3m

36- Dados --- massa da mala – m_l = 20 kg --- velocidade da mala – v_l = 4 m/s --- massa do carrinho – m₂ = 60 kg --- velocidade do carrinho – v₂ = 0 --- velocidade final do sistema (m₁ + m₂) – V --- observe que o sistema é mecanicamente isolado apenas nadireção horizontal --- assim, só há conservação da Quantidade de Movimento (ou Momento Linear) apenas nessa direção --- Q_antes = Q_depois --- m₁v₁ + m₂v₂ = (m₁ + m₂)V --- 20(4) + 60(0) = (20 + 60)V --- 80 = 80V --- V = 1 m/s --- quanto a Energia Mecânica, seria desnecessário cálculo, pois pode-se analisar esse caso como uma colisão inelástica (os corpos seguem juntos), onde há dissipação de Energia Mecânica (a Energia Mecânica só se conserva em choques perfeitamente elásticos) --- provando --- como a altura não varia ocorre apenas variação de energia cinética --- E_mi=m₁V₁²/2=20x4²/2 --- E_mi=160J --- E_mf=(m₁ + m₂)V²/2 =80x1²/2=40J --- a energia mecânica passou de 120J para 40J, ou seja, diminuiu --- R- C

37- Dados --- M_G = 300 g --- M_M = 100 g --- V_G = 80 km/h --- V_M = 24 km/h --- antes da caça, os módulos das quantidades de movimento do gavião e do melro são, respectivamente --- Q_G = 300 (80) g.km/h=24.000gkm/h --- Q_M = 100 (24) g. km/h ---Q_M=2.400gkm/h --- como ocorre conservação da quantidade de movimento no momento da caça, o vetor velocidade tem a

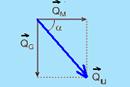
mesma direção da quantidade de movimento do sistema gavião-melro --- observe na figura que tgα=cateto oposto/cateto adjacente --- tgα=Q_G/Q_M=24.000/2.400 --- tgα=10 --- R- B

38- a) Se você considerar o sistema carro-ônibus como um sistema isolado, você pode utilizar o teorema da conservação da

quantidade de movimento --- Q_antes=M.V_o + m_a.V_a=9000.80 +1000.0 --- Q_antes=720000kg.m/s --- Q_depois=(M + m_a).V=10.000.V

Q_depois=10000V --- Q_antes = Q_depois --- 720000=10000V --- V=72km/h.

b) Pela figura fornecida você pode determinar a intensidade da força lateral --- sen3^o=F_L/F_at --- 0,05=F_L/8000 --- F_L=400N

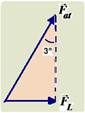
A aceleração lateral do carro tem intensidade --- F_L=m.a_L --- 400=1600.a_L --- a_L=0,25m/s²