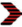
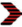
COMPOSIÇÃO DE MOVIMENTOS
Você
está olhando de
cima a carroceria de um caminhão que está em repouso.
Sobre a carroceria você está vendo uma
bola que está se movendo com velocidade
,
em relação à mesma (carroceria), na direção e sentido indicados
na figura. Essa velocidade
é
chamada de velocidade relativa.
Em
seguida, o caminhão adquire
movimento retilíneo e uniforme de direção
horizontal e sentido para
a
direita,
com velocidade 
em
relação à Terra.
Essa velocidade é chamada de velocidade
de arrastamento.
Segundo o princípio da independência de movimentos (Galileu Galilei) a bola apresentará dois movimentos parciais:
O
primeiro
em
relação à carroceria ()
e o segundo,
provocado pelo deslocamento do caminhão
(
).
A
velocidade
da bola em relação à Terra
(vista por uma pessoa na Terra), que é chamada de velocidade
resultante,
será 
,
tal que:
O que você deve saber, informações e dicas.
Concentre-se e procure entender as explicações a seguir:
Exemplos clássicos:
Um barco
desenvolve velocidade própria
(em
relação à água)
VB=4m/s
num rio em que a correnteza
tem velocidade Vc=3m/s
(velocidade da água em relação à margem).
O rio tem largura
de 100m.
Pede-se:
a)
A velocidade
(
)
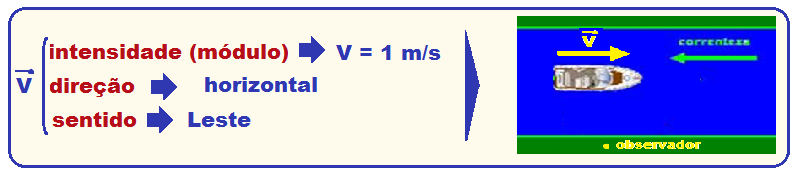
do barco em relação à margem, quando ele sobe o rio.
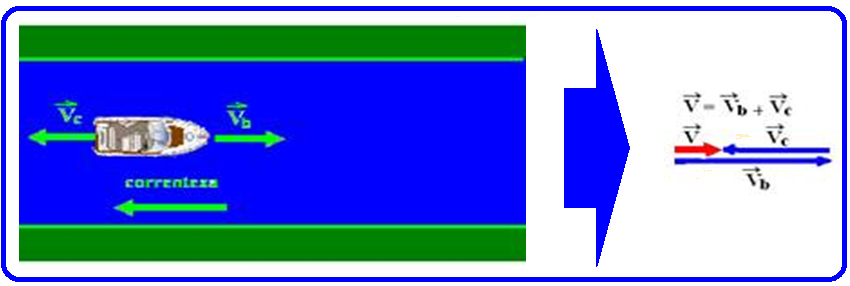
Em
módulo 
V
=
4 – 3
V
= 1m/s
(velocidade com que uma pessoa
parada na margem do rio veria o barco passar por ela, subindo o rio).
b)
A velocidade
()
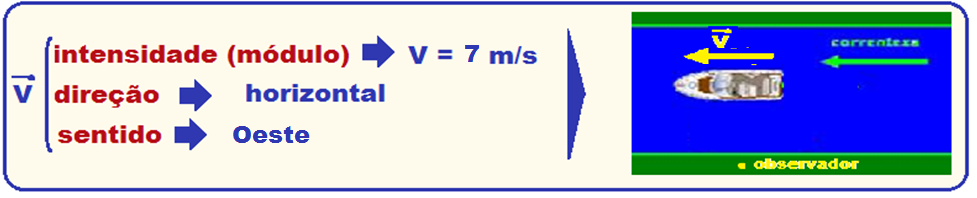
do barco em relação à margem, quando ele desce o rio.
Em
módulo
V
= 4 + 3
V
= 7m/s
(velocidade com que uma pessoa
parada na margem do rio veria o barco passar por ela, descendo o rio)
c)
A velocidade
()
do barco em relação à margem sabendo que durante a travessia seu
eixo se mantém perpendicular à mesma.
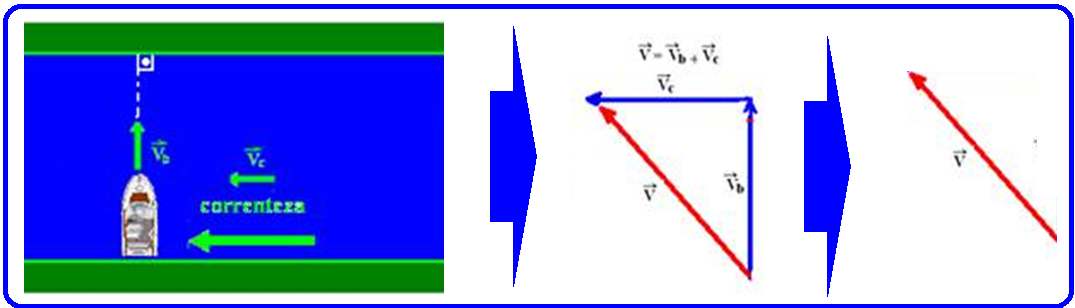
Em
módulo
V2=Vb2 +
Vc2
V=√16 + 9 V=5m/s
(velocidade do barco visto por uma pessoa
parada na margem do rio.
d) Qual é o tempo mínimo de travessia?
Esse tempo só ocorre quando o barco é colocado perpendicularmente à margem do rio (item anterior com Vb=4 m/s).
Vb
=d/tmínimo
4
= 100/tmínimo
tmínimo
= 25 s.
Lembre-se de que esse tempo não depende da velocidade da correnteza, mas apenas da velocidade do barco (Vb) e da largura do rio (d = 100m). Isso ocorre porque velocidade do barco e a velocidade da correnteza são perpendiculares entre si, e a velocidade do barco não tem componente na direção da correnteza ou seja, a correnteza não terá nenhuma influência no tempo que o barco gasta para atravessar o rio; haja ou não correnteza o tempo de travessia será o mesmo, pois o efeito da correnteza é unicamente o de deslocar o barco rio abaixo.
Da mesma maneira, sendo nula a componente da velocidade do barco na direção da correnteza, a velocidade do barco não terá influência no seu deslocamento (da correnteza) rio abaixo.
e) Determine, com o eixo perpendicular à margem, a distância que o barco percorre rio abaixo, ou seja, a distância XY (figura).
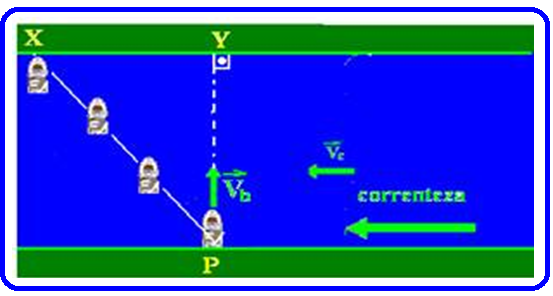
Essa
distância
é devida apenas à velocidade da correnteza de valor Vc
=
3m/s Vc=ΔS/Δt
3=XY/25 XY=75m.
f) Qual é a distância total que o barco percorre (distância PX) do item anterior?
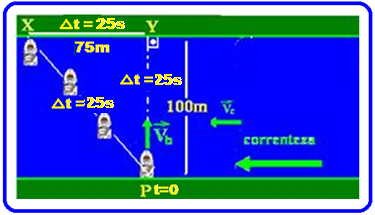
Você pode calcular essa distância (PX) de duas maneiras:
Aplicando o teorema
de Pitágoras
no triângulo retângulo
(PX)2
= (PY)2
+ (XY)2
= 1002
+ (75)2
=
10000
+ 5625
(PX)
= √(15625)
(PX)
= 125 m.
Na direção
(PX)
a velocidade do barco tem intensidade V
= 5 m/s
e percorre essa distância em ∆t
=
25s
V
= ∆S/∆t
5 = (PX)/25
PX = 5.25
PX
= 125m.
g)
Qual
deve ser a velocidade
()
do barco em relação à margem
de modo que a distância
percorrida
durante a travessia seja mínima?
Que ângulo
o barco deve estar inclinado em relação à perpendicular à margem?
Para
que a distância
percorrida seja mínima
o barco deve atravessar
o rio perpendicularmente, ou
seja, pelo
caminho PY (menor distância entre as margens)
e, para que isso ocorra o barco
deve estar
posicionado
conforme a figura abaixo.
Assim, a velocidade
resultante ()
deve ser perpendicular à margem de modo que 
forme
um ângulo β com ,
tal que:
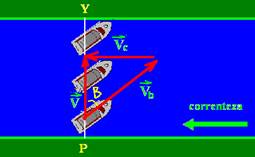
Cálculo
da intensidade de
aplicando Pitágoras no triângulo retângulo Vb2
=
V2 +
Vc2 ---
42
=
V2 +
9 V=√7=2,6m/s
senβ
= Vc/Vb
=
3/4
β
– arco cujo seno é 3/4.
Um esquiador está parado na neve e observa que os flocos de neve caem verticalmente com velocidade de 7,2km/h em relação ao solo.
Em seguida, ele entra em movimento horizontal para a direita com velocidade V=36km/h em relação ao solo.
Calcule a velocidade Vfe dos flocos em relação ao esquiador.
Observe que a velocidade dos flocos quando o esquiador está parado, que é vertical, fica inclinada quando ele entra em movimento.
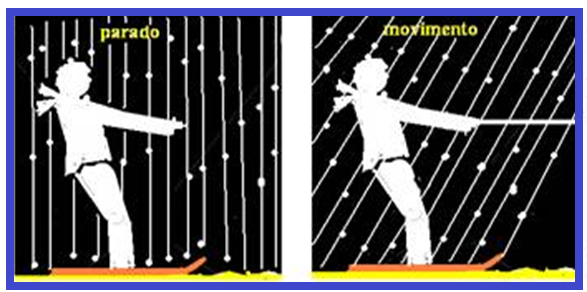
Movimento
dos flocos
em
relação ao solo (movimento resultante) Vfs
=
7,2km/h/3,6 =
2m/s.
Movimento
do esquiador
em
relação ao solo (movimento de arrastamento) Ves
=
36km/h/3,6 = 10m/s.
É pedido o movimento dos flocos em relação ao esquiador Vfe (movimento relativo). Veja figura:
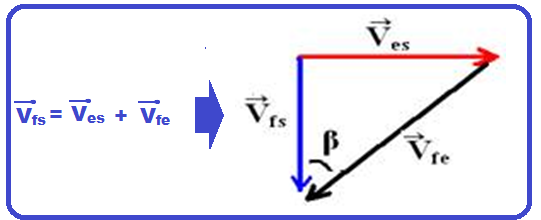
Aplicando
Pitágoras
(Vfe)2 =
(2)2 +
(10)2 Vfe=10,2
m/s.
Direção
que os flocos de neve formam com a vertical tgβ
= Ves/Vfs
=
10/2
β=arco
cuja tangente é 5.
Considere um carro
se movendo numa estrada plana e horizontal com velocidade de
intensidade
V.
As rodas
desse carro rolam sem
escorregar.
O ponto
0
corresponde ao eixo
da roda,
que tem a mesma
velocidade que o carro em relação ao solo, e velocidade nula em
relação ao carro.
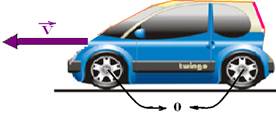
Observe que:
O único
ponto da roda
que está em repouso
em relação ao carro é o ponto
0 e que possui a mesma velocidade V que o carro.
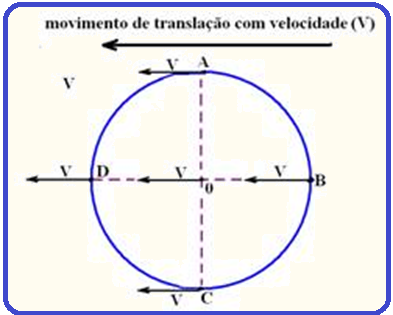
No movimento
de translação,
com o carro se movendo para a esquerda
com velocidade de
intensidade
V,
todos
os pontos da roda
nesse deslocamento também
possuem velocidade V.
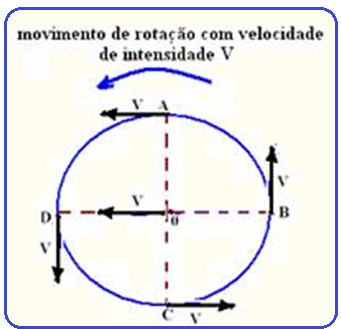
Devido à rotação em torno de 0, todos os pontos da periferia (parte externa) da roda devem ter a mesma velocidade de intensidade V, que é sempre tangente em cada ponto e orientadas no sentido de rotação da roda (no caso, anti-horário, pois o carro de desloca para a esquerda).
Efetuando a composição dos dois movimentos, de rotação e de translação:
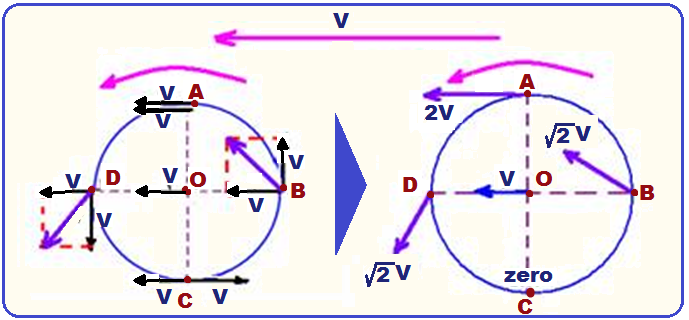
Intensidade da velocidade resultante nos pontos 0, A, B, C e D:
Veja na figura abaixo, a intensidade da velocidade de translação dos pontos 0, A e C de uma das rodas do carro, que está se movendo para a esquerda com velocidade V:
Considere uma
pessoa
que tem entre
as palmas de suas mãos um cilindro de eixo C horizontal.
Admita
que
em determinado instante as mãos da pessoa estejam dotadas de
movimentos
verticais, com a mão esquerda (mão A) descendo, com velocidade de
intensidade 8,0 cm/s, e a mão direita (mão B) subindo, com
velocidade de intensidade 12 cm/s, conforme representa o esquema.
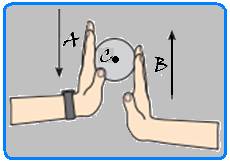
Supondo que não haja escorregamento do cilindro em relação às mãos, determine no instante considerado as características (intensidade, direção e sentido) da velocidade do eixo C.
Veja as velocidades dos pontos O, A e C (V0 = V, VA = 2V e VC = 0) das rodas do carro estudadas acima e compare-as com o cilindro desse exemplo.
Observe nas figuras abaixo que devido somente à mão A (a B parada), o centro do cilindro (ponto C)
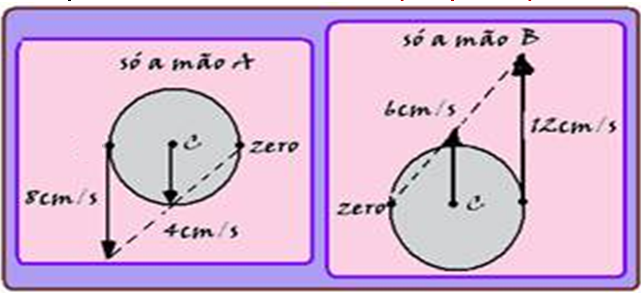
desceria com V1=4cm/s e que, devido somente à mão B (a A parada) ele subiria com V2=6cm/s. Superpondo os efeitos provocados por cada mão você obterá o efeito resultante e o eixo C subirá com velocidade de intensidade Vc = 6 – 4 =2cm/s, direção vertical e sentido para cima.
Como
se locomove um trator de esteira ou um tanque de guerra com esteira
O trator de esteira é um trator comum, e a única diferença é que no lugar de ter pneus para se locomover foram colocadas esteiras, o que garante uma maior aderência ao solo, e ainda uma melhor distribuição de peso quando está sendo operado em solos onde a terra é solta, também em terrenos pantanosos.
Possui grande facilidade de se mover em terrenos irregulares, não deslizam e, por esses motivos, também são utilizados como tanques de guerra.
A figura representa um trator de esteira. Os roletes estão acoplados ao motor e giram em movimento circular uniforme com a mesma velocidade angular W. A diferença de velocidade relativa entre as partes da esteira é responsável pelo movimento do trator.
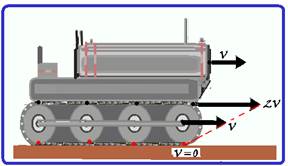
Em relação ao solo, o corpo do trator e cada um dos eixos de seus roletes que estão fixos no trator, avançam com velocidade V. Todos os pontos da parte superior da esteira se movem com velocidade 2V e todos os pontos da parte inferior da esteira, em contato com o solo, tem velocidade nula.
Observe que ele não desliza porque todos os pontos da parte inferior da esteira estão em repouso em relação ao solo e que a velocidade dos pontos da esteira variam de zero até 2V.
Exemplo numérico para que
você entenda:
O trator de esteira esquematizado na figura está em movimento retilíneo e uniforme para a direita,
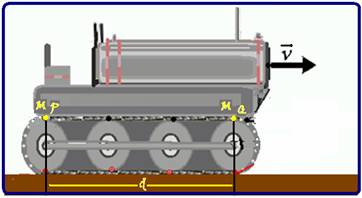
com velocidade de módulo v. Suponha que não ocorra deslizamento da esteira em relação ao solo nem da esteira em relação aos roletes.
Os roletes são idênticos, possuem raio R = 20 cm e giram em torno dos respectivos eixos que estão acoplados ao motor, o qual gira o eixo de cada rolete com a mesma frequência.
Sabendo que uma mancha M da esteira (indicada na figura) gasta 1 s para deslocar-se do ponto P até o ponto Q, e que nesse deslocamento ela percorre 8m em relação ao solo, calcule:
a) o valor da velocidade v do corpo do trator (que é a mesma que a de cada um dos eixos), bem como o comprimento d indicado na figura;
b) a frequência de rotação de cada rolete em relação ao trator. (considere π = 3).
a) A mancha M da parte superior da esteira (assim como qualquer ponto da mesma) quando se move
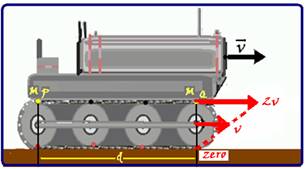
de P para Q, se desloca com velocidade 2v em relação ao solo, percorrendo ∆S=8m, também em
relação ao solo, no intervalo de tempo ∆t = 1 s.
Com
os dados
acima
você vai calcular a velocidade
V do corpo do trator
que é a mesma
para cada
eixo
do rolete
V
= ∆S/∆t
2v=8/1 v
= 4 m/s
x 3,6 =
14,4 km/h
(velocidade
do corpo trator e de
cada
eixo de cada rolete).
Distância d percorrida pelo corpo do trator que se desloca com velocidade V = 4 m/s no intervalo de
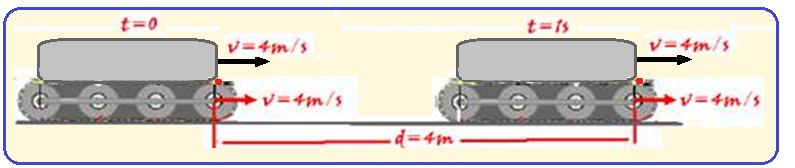
tempo
de ∆t
= 1s
v=d/∆t
4=d/1
d=4m.
b) Em relação ao trator, todos os pontos da periferia de cada rolete giram com a mesma velocidade escalar (linear) v, que é a mesma que do trator v = 4 m/s.
Numa
volta completa
∆S=2πR=2x3x0,2 ∆S=1,2m V=∆S/∆t V=∆S/T
4=1,2/T T
= 0,3s
(T período, tempo que cada rolete demora para efetuar uma volta completa).
A
frequência f
pedida é o inverso
do período T
f
= 1/T
=
(1/0,3) Hz
f=(1/0,3)x60 f=200rpm.
Baseado
na figura abaixo, considere:
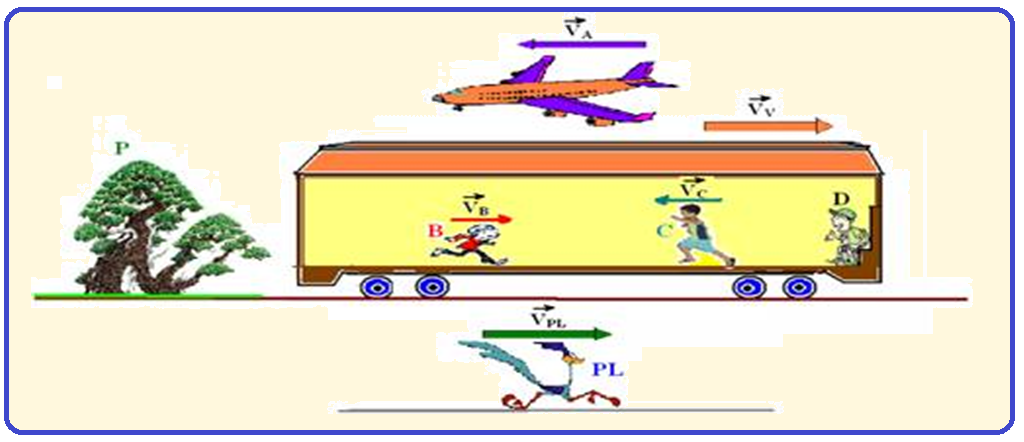
VA=500km/h
módulo da velocidade do avião
em relação à Terra
VV=100km/h
módulo da velocidade do vagão
em relação à Terra
VB=3km/h
módulo da velocidade de B
em relação ao vagão
VC=2km/h
módulo da velocidade de C
em relação ao vagão
D
uma pessoa
em repouso em relação ao vagão
P
uma
árvore
VPL=80km/h
módulo da velocidade
de PL em relação à Terra
Baseado nos dados acima, procure entender as velocidades relativas entre:
a)
Vagão e P
VVP=100km/h
(a
distância entre o vagão e a árvore varia (aumenta) na razão de
100km/h.
b)
B e o Vagão
VBV=3km/h (a
distância entre B e qualquer ponto fixo no vagão varia na razão de
3 km/h).
c)
Vagão e B
VVB=3km/h
(a
distância entre qualquer ponto fixo no vagão e Bvaria na razão de
3 km/h). Observe
que VBV
e
VVB
tem o mesmo módulo de 3 km/h.
d)
B e D
VBD=3km/h
(a
distância entre B e D varia na razão de 3 km/h).
e)
D e P
VDP=100km/h (a
distância entre D e P varia na razão de 100 km/h).
f)
B e C
VBC=5km/h (a
distância entre B e C varia (aumenta) numa razão de (2 + 3) = 5
km/h).
g)
C e B
VCB=5km/h (veja
f).
h)
D e PL
VDPL=20km/h
(a
distância entre D e PL varia na razão de (100 – 80) = 20 km/h)
i)
Vagão e A
VVA=600km/h (a
distância entre
o
vagão e e o avião está variando (aumentando) na razão de (500 +
100) = 600 km/h).
j)
B e P
VBP=103km/h (a
distância entre
o
vagão e e o avião está variando (aumentando) na razão de (3 +
100) = 103 km/h).
l)
P e C
VPC=98km/h
(a
distância entre
P
e C e o avião está variando (aumentando) na razão de (100 - 2) =
98 km/h).
m)
B e PL
VBPL=23km/h
n)
B e A
VBA=603km/h
o)
C e PL
VCPL=18km/h
p)
A e C
VAC=598km/h
Um menino
está sobre um vagão-prancha de 10
m de comprimento,
que se desloca
sobre trilhos retilíneos com velocidade
constante de módulo 36 km/h em relação ao solo.
Em certo
momento,
o menino
começa a se deslocar da parte
de trás
do vagão e alcança a sua frente
após 5,0 s, com passadas regulares.
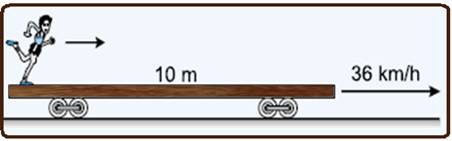
Vamos calcular, para o intervalo de tempo considerado:
I. O módulo do deslocamento do menino em relação ao vagão.
Vamos observar apenas o menino e o vagão, podendo considerar o vagão parado.
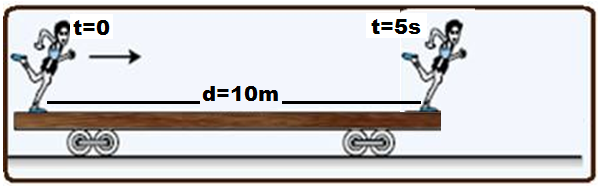
Quando o menino chega ao final do vagão a distância entre um ponto fixo no menino e um ponto fixo no início do vagão variou de d=10m.
II.O módulo da velocidade do menino, em relação ao vagão.
Vamos observar apenas o vagão e o menino. Assim, a distância entre um ponto fixo no menino e um ponto fixo no início do vagão está variando na razão de d=10m em ∆ t=5s e, assim, o módulo da velocidade do menino em relação ao vagão é de V= d/∆t = 10/5 = 2m/s.
II. O módulo da velocidade do menino em relação ao solo.
Uma pessoa parada no solo verá o menino se deslocando para a direita com velocidade de 2m/s
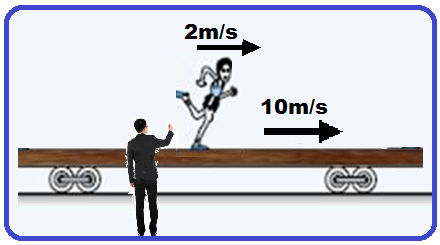
mais o vagão também se deslocando para a direita com velocidade de 10m/s .
Portanto a distância entre um ponto fixo no solo e um ponto fixo no menino estará variando com velocidade de V=2 + 10=12m/s.
Exercícios de vestibulares sobre Composição de Movimentos
01-(FUVEST-SP) Num vagão ferroviário, que se move com velocidade Vo=3ms com relação aos trilhos,estão dois meninos que correm um em direção ao outro, cada um com velocidade V=3m/s, com relação ao vagão.
A velocidade dos meninos VA e VB, com relação aos trilhos, será, respectivamente:
02-(UNESP-SP) Entre duas cidades X e Y, sopra um vento de 50 km/h na direção indicada na figura. Um avião, que desenvolve 250 km/h em relação ao ar, faz em linha reta a trajetória XY. Qual das retas abaixo melhor indica (no plano horizontal de vôo), a inclinação do avião em relação à trajetória XY?
03-(Univale-MG) Um ultraleve mantém a velocidade de 120km/h em relação ao ar, mantendo o nariz apontando para o Leste.
Sopra vento Sul com velocidade de 90km/h. Nessas condições, podemos afirmar que a velocidade do ultraleve em relação à Terra é:
a) 150km/h, na direção sudeste
b) 30km/h, na direção Leste
c) 210km/h, na direção sudoeste
d) 50km/h, na direção Nordeste
e) 210km/h, na direção Sudeste
04-(UFBA) Um pássaro parte em vôo retilíneo e horizontal do seu ninho para uma árvore distante 75m e volta, sem interromper o vôo, sobre a mesma trajetória.
Sabendo-se que sopra um vento de 5m/s na direção e sentido da árvore para o ninho e que o pássaro mantém, em relação à massa de ar, uma velocidade constante de 10m/s, determine, em segundos, o tempo gasto na trajetória de ida e volta.
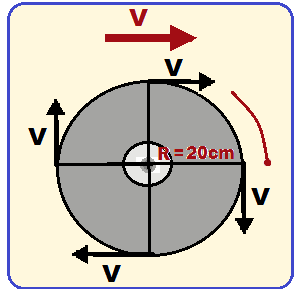
05-(FUVEST-SP)
Um disco roda sobre uma superfície plana, sem deslizar. A velocidade
do centro O é 
.
Em relação ao plano:
a)
Qual a velocidade 
do
ponto A?
b)
Qual a velocidade 
o
ponto B?
06-(FEI-SP) Um avião voa com velocidade Va=300km/h constante do norte para o sul. Em dado momento ele entra em uma região onde o vento sopra com velocidade VV=150√3km/h de leste para oeste. Qual deverá ser o ângulo de correção da rota com a direção norte-sul que o avião deverá fazer para chegar a uma cidade situada a 200km ao sul do ponto de partida?
07-(FGV-SP) Um patrulheiro viajando em um carro dotado de radar a uma velocidade de 60 km/h em relação a um referencial fixo no solo, é ultrapassado por uma caminhonete que viaja no mesmo sentido que ele.
A velocidade indicada pelo radar após a ultrapassagem é de 30 km/h. A velocidade da caminhonete em relação ao solo é, em km/h, igual a:
08-(CEFET) Numa represa um homem faz seu barco a remo atingir uma velocidade máxima de 8 quilômetro por hora.
Se esse mesmo remador estiver num rio cujas águas correm para o oeste com uma velocidade de 5 quilômetros por hora, determine a velocidade máxima que ele consegue atingir quando:
a) rema no mesmo sentido da correnteza.
b) rema no sentido oposto ao da correnteza.
09-(UFB) Numa represa um homem faz seu barco a remo atingir uma velocidade máxima de 8 quilômetros por hora.
Nesse mesmo remado tenta atravessar um rio cujas águas se movem com uma velocidade de 5 quilômetros por hora como indica a figura a seguir. O rio tem largura de 3,2 km.
Se o barco parte do ponto A, em qual ponto da outra margem o barco chegará?
10-(UERJ-RJ) Um barco percorre seu trajeto de descida de um rio, a favor da correnteza, com a velocidade de 2m/s em relação à água. Na subida, contra a correnteza, retornando ao ponto de partida, sua velocidade é de 8 m/s, também em relação à água.
Considere que:
- o barco navegue sempre em linha reta e na direção da correnteza;
- a velocidade da correnteza seja sempre constante;
- a soma dos tempos de descida e de subida do barco seja igual a 10 min.
Assim, a maior distância, em metros, que o barco pode percorrer, neste intervalo de tempo, é igual a:
11-(UFMS-MS) Um carro move-se com velocidade constante de 60 km/h. Começa a chover e o motorista observa que as gotas de água da chuva caem formando um ângulo de 30° com a vertical.
Considerando que, em relação à Terra, as gotas caem verticalmente, qual a velocidade em que as gotas de água caem em relação ao carro?
12-(Ufjf-MG) Um homem parado numa escada rolante leva 10 s para descê-la em sua totalidade.
O mesmo homem leva 15 s para subir toda a escada rolante de volta, caminhando contra o movimento dela. Quanto tempo o homem levará para descer a mesma escada rolante, caminhando com a mesma velocidade com que subiu?
13-(CEFET-CE) Partindo de um ponto A das margens de um rio, um barco, que pode desenvolver velocidade constante Vb de 4,5 m/s, em relação às águas do rio, atinge a outra margem no ponto C, imediatamente oposto, arrastado pela correnteza, quando segue em direção a B.
Considere as margens do rio paralelas e despreze qualquer ação do vento.
Sabendo que as distâncias AC e BC valem, respectivamente, 400 m e 300 m, determine o módulo:
a) da velocidade de arraste do rio (Varr).
b) da velocidade do barco em relação às margens (Vres).
14-(MACKENZIE-SP) Um passageiro em um trem, que se move para a sua direita em movimento retilíneo uniforme, observa a chuva através da janela. Não há ventos e as gotas de chuva já atingiram a velocidade limite. O aspecto da chuva observado pelo passageiro é:
15-(UFMT) Uma pessoa tem velocidade, relativa a uma esteira, de módulo 1,5m/s e direção perpendicular à da velocidade de arrastamento da esteira.
A largura da esteira é de 3,0m e sua velocidade de arrastamento, em relação ao solo em relação ao solo, tem módulo igual a 2,0m/s. Calcule:
a) o módulo da velocidade da pessoa, em relação ao solo.
b) a distância percorrida pela pessoa, em relação ao solo, ao atravessar a esteira.
16- (UFMG-MG) Dois barcos - I e II - movem-se, em um lago, com velocidade constante, de mesmo módulo, como representado na figura:
Em relação à água, a direção do movimento do barco I é perpendicular à do barco II e as linhas tracejadas indicam o sentido do deslocamento dos barcos.
Considerando-se essas informações, é CORRETO afirmar que a velocidade do barco II, medida por uma pessoa que está no barco I, é mais bem representada pelo vetor
17-(UFMG-MG) Um menino flutua em uma bóia que está se movimentando, levada pela correnteza de um rio. Uma outra bóia, que flutua no mesmo rio a certa distância do menino, também está descendo a correnteza. As posição das duas bóias e o sentido da correnteza estão indicados na figura.
Considere que a velocidade da correnteza é a mesma em todos os pontos do rio.Nesse caso, para alcançar a segunda bóia, o menino deve nadar na direção indicada pela linha:
18-(FUVEST-SP) Um navio desloca-se na direção norte-sul com movimento retilíneo e uniforme de velocidade 10m/s.
Um passarinho, pousado numa das paredes do navio, levanta vôo na direção leste-oeste, com velocidade constante de 20m/s em relação ao navio. Para um observador parado no navio, o pássaro:
a) voa na direção leste-oeste com velocidade √500m/s
b) voa na direção aproximada do sudoeste, com velocidade de √500m/s
c) voa na direção leste-oeste com velocidade de 20m/s
d) voa na direção sudoeste com velocidade de √200m/s
e) está em repouso.
19-(UFPE-PE) Um barco de comprimento L = 80 m, navegando no sentido da correnteza de um rio, passa sob uma ponte de largura D = 25 m, como indicado na figura.
Sabendo-se que a velocidade do barco em relação ao rio é Vb = 14 km/h, e a velocidade do rio em relação às margens é VR = 4 km/h, determine em quanto tempo o barco passa completamente por baixo da ponte, em segundos.
20-(UFMG-MG) Um barco tenta atravessar um rio com 1,0km de largura. A correnteza do rio é paralela às margens e tem velocidade de 4,0km/h. A velocidade do barco, em relação à água, é de 3,0km/h perpendicularmente às margens. Nessas condições pode-se afirmar que o barco:
a) atravessará o rio em 12 minutos
b) atravessará o rio em 15 minutos
c) atravessará o rio em 20 minutos
d) atravessará o rio em 6 minutos
e) nunca atravessará o rio
21-(PUC-RJ) Um avião em vôo horizontal voa a favor do vento com velocidade de 180 km/h em relação ao solo.
Na volta, ao voar contra o vento, o avião voa com velocidade de 150 km/h em relação ao solo. Sabendo-se que o vento e o módulo da velocidade do avião (em relação ao ar) permanecem constantes, o módulo da velocidade do avião e do vento durante o vôo, respectivamente, são:
a) 165 km/h e 15 km/h
b) 160 km/h e 20 km/h
c) 155 km/h e 25 km/h
d) 150 km/h e 30 km/h
e) 145 km/h e 35 km/h
22-(PUC-RS) Um avião, voando a 240m/s em relação ao ar, numa altitude onde a velocidade do som é de 300m/s, dispara um míssil que parte a 260m/s em relação ao avião. Assim, as velocidades do míssil em relação ao ar e da onda sonora originada no disparo serão, respectivamente,
a) 260m/s e 40m/s.
b) 260m/s e 60m/s.
c) 260m/s e 300m/s.
d) 500m/s e 300m/s
e) 500m/s e 540m/s.
23-(UFPI) Uma prancha está apoiada sobre dois cilindros paralelos, idênticos e dispostos sobre uma superfície horizontal.
Empurrando a prancha com velocidade constante e considerando inexistente qualquer tipo de deslizamento, seja entre a prancha e os cilindros, seja entre os cilindros e a superfície horizontal, a relação VP/VC, entre a velocidade da prancha, VP, e a velocidade do cilindro, VC, será:
24-(UFMS-MS) Seja um rio sem curvas e de escoamento sereno sem turbulências, de largura constante igual a L. Considere o escoamento representado por vetores velocidades paralelos às margens e que cresce uniformemente com a distância da margem, atingindo o valor máximo vmáx no meio do rio. A partir daí a velocidade de escoamento diminui uniformemente atingindo o valor nulo nas margens. Isso acontece porque o atrito de escoamento é mais intenso próximo às margens. Um pescador, na tentativa de atravessar esse rio, parte da margem inferior no ponto O com um barco direcionado perpendicularmente às margens e com velocidade constante em relação à água, e igual a u. As linhas pontilhadas, nas figuras, representam possíveis trajetórias descritas pelo barco ao atravessar o rio saindo do ponto O e chegando ao ponto P na margem superior. Com fundamentos nos conceitos da cinemática, assinale a alternativa CORRETA.
a) A figura A representa corretamente a trajetória do barco; e o tempo t para atravessar o rio é igual a t = L/(vmáx+u).
b) A figura B representa corretamente a trajetória do barco; e o tempo t para atravessar o rio é igual a t = L/u.
c) A figura C representa corretamente a trajetória do barco; e o tempo t para atravessar o rio é igual a t = L/u.
d) A figura B representa corretamente a trajetória do barco; e o tempo t para atravessar o rio é igual a t = L/(u+vmáx).
e) A figura D representa corretamente a trajetória do barco; e o tempo t para atravessar o rio é igual a t = L/u.
25-(ITA-SP) Um barco leva 10 horas para subir e 4 horas para descer um mesmo trecho do rio Amazonas, mantendo constante o módulo de sua velocidade em relação à água. Quanto tempo o barco leva para descer esse trecho com os motores desligados?
a) 14 horas e 30 minutos
b) 13 horas e 20 minutos
c) 7 horas e 20 minutos
d) 10 horas
e) Não é possível resolver porque não foi dada a distância percorrida pelo barco.
26-(UFAL-AL) De dentro de um automóvel em movimento retilíneo uniforme, numa estrada horizontal, um estudante olha
pela janela lateral e observa a chuva caindo, fazendo um ângulo (θ) com a direção vertical, com senθ= 0,8 e cos θ= 0,6.
Para uma pessoa parada na estrada, a chuva cai verticalmente, com velocidade constante de módulo v. Se o velocímetro do automóvel marca 80,0 km/h, pode-se concluir que o valor de v é igual a:
a) 48,0 km/h
b) 60,0 km/h
c) 64,0 km/h
d) 80,0 km/h
e) 106,7 km/h
27-(UECE-CE) Um barco pode viajar a uma velocidade de 11 km/h em um lago em que a água está parada.
Em um rio, o barco pode manter a mesma velocidade com relação à água. Se esse barco viaja no Rio São Francisco, cuja velocidade da água, em relação à margem, assume-se 0,83 m/s, qual é sua velocidade aproximada em relação a uma árvore plantada na beira do rio quando seu movimento é no sentido da correnteza e contra a correnteza, respectivamente?
a) 14 km/h e 8 km/h.
b) 10,2 m/s e 11,8 m/s.
c) 8 km/h e 14 km/h.
d) 11,8 m/s e 10,2 m/s.
28-(UFPR-PR) Segundo o grande cientista Galileu Galilei, todos os movimentos descritos na cinemática são observados na natureza na forma de composição desses movimentos. Assim, se um pequeno barco sobe o rio Guaraguaçu, em Pontal do
Paraná, com velocidade de 12 km/h e desce o mesmo rio com velocidade de 20 km/h, a velocidade própria do barco e a velocidade da correnteza serão, respectivamente:
a) 18 km/h e 2 km/h.
b) 17 km/h e 3 km/h.
c) 16 km/h e 4 km/h.
d) 15 km/h e 5 km/h.
e) 19 km/h e 1 km/h.
29-(UFRN-RN) Considere um grande navio, tipo transatlântico, movendo-se em linha reta e com
velocidade constante (velocidade de cruzeiro). Em seu interior, existe um salão de jogos climatizado e nele uma mesa de pingue-pongue orientada paralelamente ao comprimento do navio. Dois jovens resolvem jogar pingue-pongue, mas discordam sobre quem deve ficar de frente ou de costas para o sentido do deslocamento do navio. Segundo um deles, tal escolha influenciaria no resultado do jogo, pois o movimento do navio afetaria o movimento relativo da bolinha de pingue-pongue.
Nesse contexto, de acordo com as Leis da Física, pode-se afirmar que
A) a discussão não é pertinente, pois, no caso, o navio se comporta como um referencial não inercial, não afetando o movimento da bola.
B) a discussão é pertinente, pois, no caso, o navio se comporta como um referencial não inercial, não afetando o movimento da bola.
C) a discussão é pertinente, pois, no caso, o navio se comporta como um referencial inercial, afetando o movimento da bola.
D) a discussão não é pertinente, pois, no caso, o navio se comporta como um referencial inercial, não afetando o movimento da bola.
30-(UNICAMP-SP) Quando um carro não se move diretamente na direção do radar, é preciso fazer uma correção da velocidade medida pelo aparelho (Vm) para obter a velocidade real do veículo (Vr). Essa correção pode ser calculada a partir da fórmula
Vm = Vr ⋅ cos(α) , em que α é o ângulo formado entre a direção de tráfego da rua e o segmento de reta que liga o radar ao ponto da via que ele mira. Suponha que o radar tenha sido instalado a uma distância de 50 m do centro da faixa na qual o carro trafegava, e tenha detectado a velocidade do carro quando este estava a 130 m de distância, como mostra a figura abaixo.
Se o radar detectou que o carro trafegava a 72 km/h, sua velocidade real era igual a
a) 66,5 km/h.
b) 36 3 km/h.
c) 78 km/h.
d) 144/3 km/h.
31-(UPE-PE)
Considere um rio de margens paralelas, cuja distância entre as margens é de 140 m. A velocidade da
água em relação às margens é de 20 m/s. Um bote cuja velocidade em relação à água é 10 m/s atravessa o rio de uma margem à outra no menor tempo possível. Assinale a alternativa que corresponde a este tempo em segundos.
32-(MACKENZIE-SP)
Um avião, após deslocar-se 120 km para nordeste (NE), desloca-se 160 km para sudeste (SE). Sendo
um quarto de hora, o tempo total dessa viagem, o módulo da velocidade vetorial média do avião, nesse tempo, foi de
a) 320 km/h
b) 480 km/h
c) 540 km/h
d) 640 km/h
e) 800 km/h
33-(UNICAMP-SP)
O transporte fluvial de cargas é pouco explorado no Brasil, considerando-se nosso vasto conjunto de rios navegáveis.
Uma embarcação navega a uma velocidade de 26 nós, medida em relação à água do rio (use 1 nó = 0,5 m/s). A correnteza do rio, por sua vez, tem velocidade aproximadamente constante de 5,0 m/s em relação às margens. Qual é o tempo aproximado de viagem entre duas cidades separadas por uma extensão de 40 km de rio, se o barco navega rio acima, ou seja, contra a correnteza?
a) 2 horas e 13 minutos.
b) 1 hora e 23 minutos.
c) 51 minutos.
d) 37 minutos.
Resolução comentada dos exercícios de vestibulares sobre COMPOSIÇÃO DE MOVIMENTOS
01- R- A (veja teoria)
02- Veja a figura abaixo:
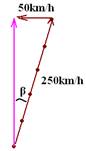
Senβ=50/250=0,2 --- β=aproximadamente 12o --- R-D
03- Aplicando Pitágoras no triângulo abaixo:
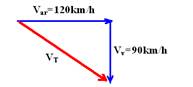
VT2=(120)2 + (90)2 --- VT=150km/h --- R- A
04- Ida do ninho para a árvore (contra o vento)---- VR=5m/s --- VR=ΔS/Δt --- 5=75/Δt --- Δt=15s --- volta da árvore para o ninho (a favor do vento) --- VR=15m/s --- VR= ΔS/Δt --- 15=75/Δt --- Δt=5s --- Δttotal=15 + 5 --- Δttotal=20s
05- R:
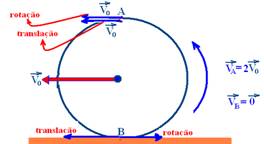
a) 
b) 
06- O avião deverá estar orientado na direção sudeste, para que ele siga a rota norte-sul
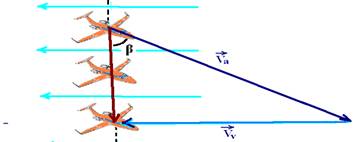
Senβ=Vv/Va=150√3/300 --- senβ=√3/2 --- β=60o --- R- D
07- Vc – velocidade da caminhonete --- velocidade do carro patrulheiro – Vp=60km/h --- o radar do carro patrulha indica a velocidade relativa – Vr=30km/h --- Vr=Vc – Vp --- 30=Vc – 60 --- Vc=90km/h --- R- E
08- a) V=8 + 5 --- V=13km/h
b) V=8 – 5 --- V=3km/h
09- Vb= ΔS/Δt --- 8= 3,2Δt --- Δt=0,4h --- nesse tempo, devido à correnteza ele se deslocou --- Vc= ΔS/Δt ---
5= ΔS/0,4 --- ΔS=2km --- chegará no ponto C.
10- Vsubida= 8 – V --- tsubida=ts --- Vsubida=d/ts --- 8 – V=d/ts --- ts=d/(8 – V) --- Vdescida=2 + V --- Vdescida=d/td --- 2 + V=d/td --- td=d/(2 + V) --- ts + td=10min --- ts + td=600 --- d/(8 – V) + d/(2 + V)=600 --- d(2 + V) + d(8 – V)=600.(8 – V).(2 + V) --- 2d + Vd + 8d – Vd = 600.(16 + 8V – 2V - V2) --- d=960 + 360V – 60V2 I --- esta é uma equação do segundo grau cujo gráfico é uma parábola e da qual se quer determinar o valor máximo para d, que ocorre no vértice da parábola, de valor Vmáximo=-B/A, onde A=-60 e B=360 (veja I) --- Vmáximo=-B/A=-360/-60 --- Vmáximo=3, que substituído em I, nos fornece a distância máxima percorrida --- dmáximo=960 +360.3 – 60.32 --- dmáximo=1500m --- R- B
11-
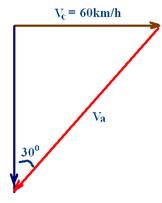
Sen30o=Vc/Va --- 1/2 =60/Va --- Va=120km/h --- R- C
12- d – comprimento da escada rolante --- parado na escada --- Ve=d/t=d/10 --- Ve=d/10 --- subindo a escada --- Vh – Ve=d/15 --- Vh – d/10=d/15 --- Vh=d/15 + d/10 --- Vh=d/6 --- descendo a escada --- Vh + Ve=d/t --- d/6 + d/10=d/t --- 10dt + 6dt=60d --- t=60/16 --- t=3,75s --- R- B
13- Observe as figuras abaixo:
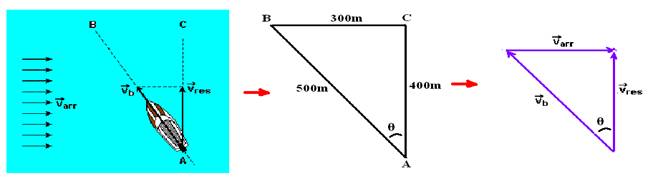
a) No triângulo ABC --- senθ=300/500 --- senθ=0,6 --- cosθ=400/500 --- cosθ=0,8 --- na figura da direita --- senθ=Varr/4,5 --- 0,6 =Varr/4,5 --- Varr=2,7m/s
b) cosθ=Vres/4,5 --- 0,8=Vres/4,5 --- Vres=3,6m/s
14- R- B (veja teoria)
15- a) veja figura abaixo
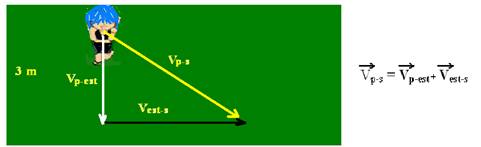
(Vp-s)2 = (Vp-est)2 + (Vest-s)2 --- (Vp-s)2=(1,5)2 + (2,0)2 --- Vp-s=2,5m/s
b) o tempo de travessia depende apenas da velocidade perpendicular à esteira (1,5m/s) e da largura da mesma (3m) ---
V=ΔS/Δt --- 1,5=3/Δt --- Δt=2s --- substituindo esse tempo em Vp-s= ΔS/Δt --- 2,5= ΔS/2 --- ΔS=5,0m
16- Se você estiver no barco I você verá o barco II se aproximar de você e, se você estiver no barco II você verá o barco I se aproximar de você --- R- C
17- Como a distância entre as duas bóias não varia, elas estão paradas uma em relação a outra. Então, o menino deve nadar diretamente de uma para outra --- R- A
18- Como o observador está em repouso no navio, a distância entre ele e o navio não varia e como o pássaro voa na direção leste-oeste em relação ao navio e consequentemente à pessoa, esta o verá voando na direção leste-oeste com velocidade de 20m/s --- R- C
19- Velocidade do barco em relação às margens --- Vb-m=14 + 4=18km/h=18/3,6=5m/s --- para atravessar totalmente a ponte o barco percorre ΔS=D + L=25 + 80=105m --- Vb-m=ΔS/Δt --- 5=105/Δt --- Δt=21s
20- Para calcular o tempo que o barco demora para atravessar o rio usa-se apenas a velocidade do barco em relação à água Vb=3,0km/h e o comprimento do rio (ΔS=1,0km) --- Vb=ΔS/Δt --- 3=1/Δt --- Δt=1/3h --- Δt=20min --- R- C
21- A favor do vento --- Va + Vv=180 I --- contra o vento --- Va – Vv=150 II --- resolvendo o sistema composto por I e II --- Va=165km/h e Vv=15km/h --- R- A
22- Vm=240 + 260 --- Vm=500m/s --- lembre-se que a velocidade do som independe da velocidade da fonte --- Vs=300m/s ---
R- D
23- A velocidade do ponto superior do cilindro que está em contato com a prancha vale 2VCe é igual à velocidade da prancha Vp, ou seja, Vp=2VC
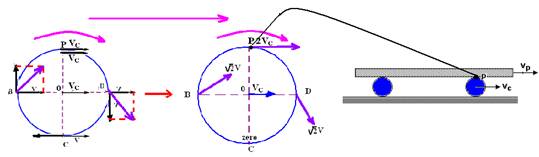
Portanto --- Vp/Vc=2 --- R- A
24- O tempo de travessia depende apenas da largura do rio (L) e da velocidade do barco em relação às margens (u) --- u=L/t --- t=L/u --- quanto maior a velocidade das águas, maior será o deslocamento do barco para a direita --- R- B
25- Subindo o rio --- V=ΔS/Δt --- Vb – Va=d/10 (I) --- descendo o rio --- V= ΔS/Δt --- Vb + Va=d/4 (II) --- fazendo (II) – (I) --- (Vb + Va) – (Vb – Va)=4/4 – d/10 --- Vb + Va – Vb + Va = (5d - 2d)/20 --- 2Va=3d/20 (III) --- descendo o rio com o motor desligado o barco percorre distância d com velocidade que é a mesma que a da água Va ---
Va=d/t --- d=Vat (IV) --- substituindo (IV) em (III) --- 2Va=3.Vat/20 --- t=40/3=13h + 1/3h --- t=13h e 20min --- R- B
26- Dados: vcarro = 80 km/h; sen q = 0,8 e cos q = 0,6 --- a figura abaixo mostra o automóvel e as velocidades do automóvel
(
)
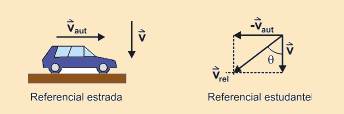
e da chuva (
),
para a pessoa parada na beira da estrada. O diagrama vetorial mostra
a composição dessas velocidades para o estudante ---
tg q =Vcarro/V
--- senq/cosq=Vcarro/V
--- 0,8/0.6=80/V --- V=60km/h --- R-
B
27- Dados: vb = 11 km/h; va = 0,83 m/s = (0,83 ´ 3,6) = 3 km/h --- na descida --- v = vb + va= 11 + 3 = 14 km/ h --- na subida
--- v = vb – va = 11 – 3 = 8 km/ h --- R- A
28- Sejam vc a velocidade da correnteza de vb a velocidade própria do barco --- na descida --- vb + vc = 20 (I) --- na subida ---
Vb – vc = 12 (II) --- somando as duas expressões --- (I) + (II) Þ (vb + vc) + (vb – vc) = 32 --- 2 vb = 32 --- vb = 16 km/h ---
Substituindo em (I) --- 16 + vc = 20 --- vc = 4 km/h --- R- C
29- Como o transatlântico se move em linha reta com velocidade constante ele está em equilíbrio dinâmico e comporta-se como se estivesse em repouso (equilíbrio estático) , não afetando o movimento da bola --- R- D
30- Observe a figura abaixo --- aplicando o Teorema de Pitágoras --- 1302 = 502 + x2 --- x =120 m --- da expressão
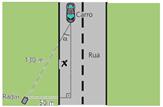
fornecida --- Vm = Vr ⋅ cos(α) --- 72=Vr.120/130 --- Vr=78km/h --- R- C
31-
O tempo mínimo de travessia só ocorre quando o bote atravessa o rio com sua velocidade (Vb=10m/s) sempre perpendicular às margens e, consequentemente perpendicular à velocidade da água (correnteza) (veja figura) --- observe que se você utilizar apenas a
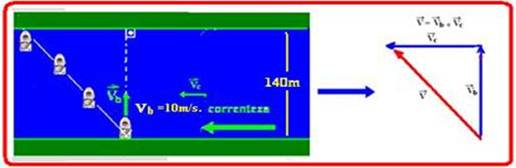
componente Vb da velocidade, a distância percorrida será a largura do rio, que é de 140m --- Vb=∆S/∆t --- 10=140/∆t --- ∆t=14s --- R- D. Observação: Esse tempo não depende da velocidade da correnteza e, dependendo dela ele apenas chegará à outra margem mais próximo ou mais afastado do ponto de partida, mas o tempo de travessia será o mesmo.
32-
Trata-se de deslocamentos vetoriais cuja representação esquemática está na figura --- observe que o triângulo é
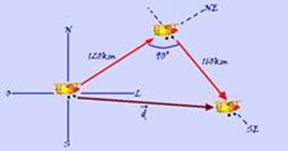
retângulo --- Pitágoras --- d2=1202 + 1602 --- d=200km --- Vm=d/∆t=200/(1/4) --- Vm=800km/h --- R- E
33-
-A
velocidade vetorial ()
do barco em relação à margem (velocidade com que uma pessoa parada
na margem do rio veria o barco passar por ela), quando ele sobe o rio
é fornecida por 
---
observe na soma vetorial abaixo que, em módulo (intensidade)
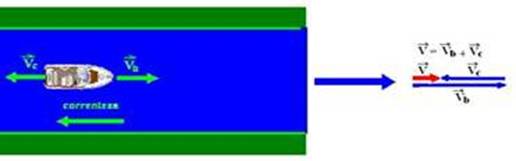
V=Vb – Vc sendo, Vb – módulo da velocidade do barco, Vc – módulo da velocidade da correnteza e V – módulo da velocidade do barco em relação à margem --- assim, no exercício V= 13 – 5 --- V=8m/s --- sendo a distância entre as duas cidades ∆S=40km=40.103m --- V=∆S/∆t --- 8=40.103/∆t --- ∆t=40.103/8=5.103 s --- ∆t = 1h 23min 20s --- R- B