Colisões Mecânicas ou Choques Mecânicos

Choques mecânicos unidimensionais são choques (colisões) que ocorrem quando os centros de massa dos corpos que interagem entre si situam-se sobre uma mesma reta, ou seja, estão sempre na mesma direção, antes e depois do choque.

Se as direções forem diversas o choque será oblíquo.

Coeficiente de restituição (e) é definido pela relação:

O coeficiente de restituição (e) é uma grandeza adimensional (não tem unidade), por ser calculado pela razão entre duas grandezas de mesma espécie e 0 < e > 1.

Cálculo do módulo da velocidade relativa:

Observações:

O resultado V_r obtido é sempre em módulo.

Se houver colisão e os corpos permanecerem unidos após a mesma, ou, se eles se moverem na mesma direção e sentido e com a mesma velocidade, tem-se evidentemente que V_X = V_Y e que V_r = 0.

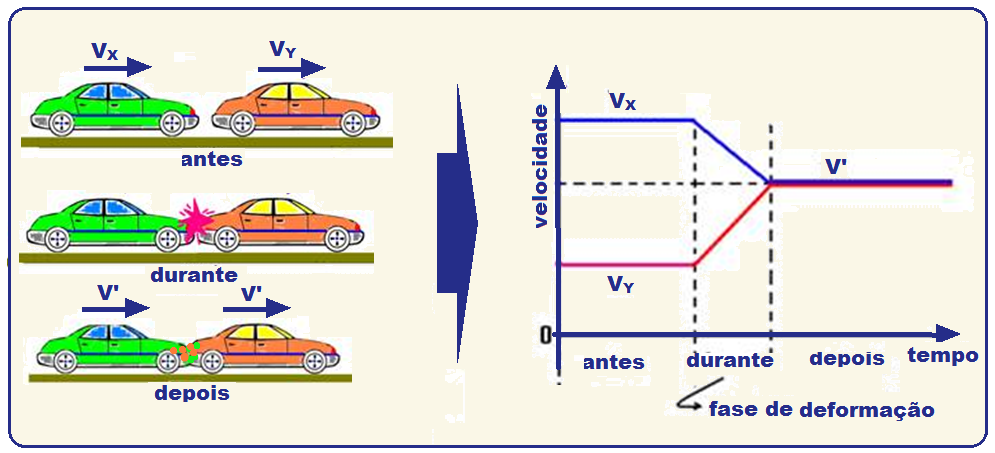
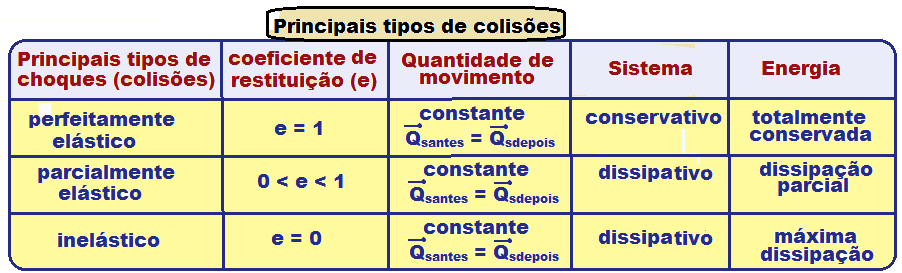
Tipos de choques

Choque perfeitamente elástico ou choque elástico

Nele, a energia é totalmente conservada (é a mesma antes e depois do choque), ou seja, o sistema é conservativo, o coeficiente de restituição é igual a 1 e a quantidade de movimento do sistema á a mesma antes e depois do choque ().

Exemplo se você abandonar de certa altura do solo uma bola e ela retornar à mesma altura, o choque dela com o solo é perfeitamente elástico ou ainda, se a bola se chocar contra uma parede

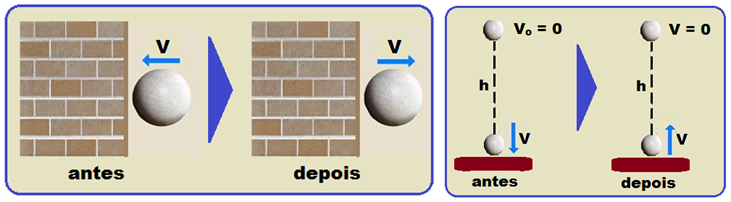
com velocidade de módulo V e retornar na mesma direção e com a mesma velocidade o choque também será perfeitamente elástico.

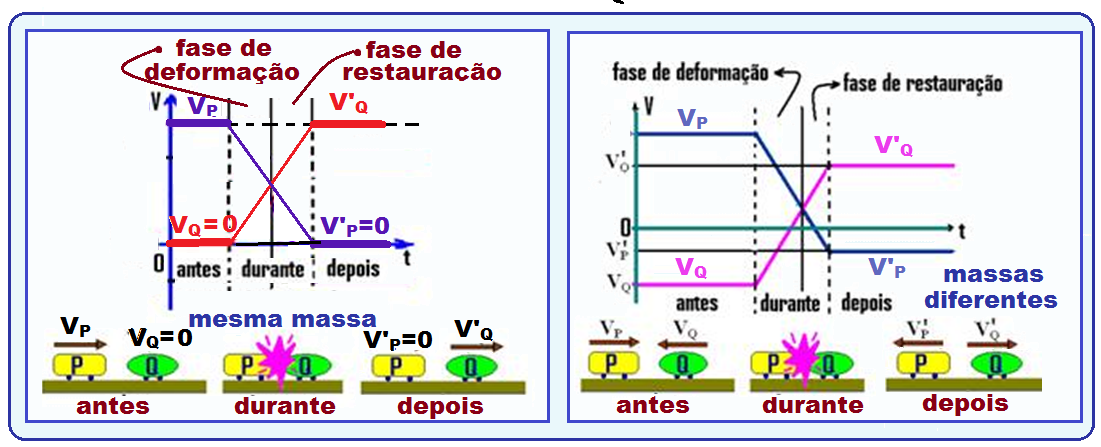
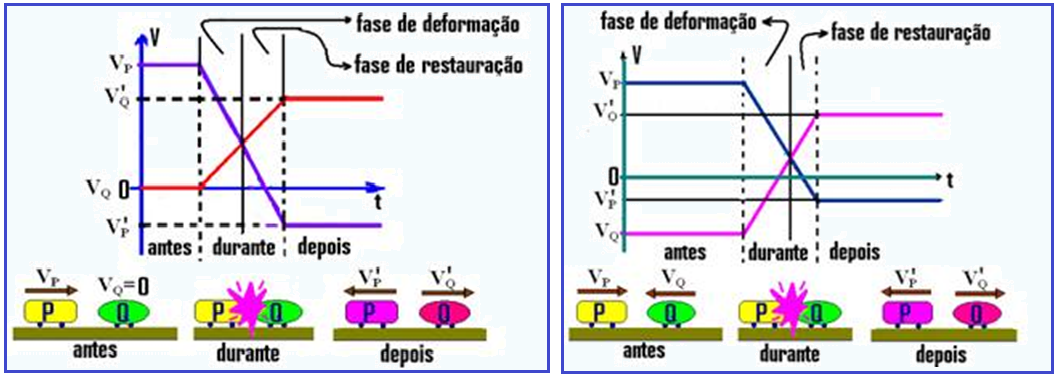
Gráficos de uma colisão perfeitamente elástica

Choque inelástico

Neste tipo de choque a dissipação de energia é máxima, o coeficiente de restituição é nulo, e, após o choque, os corpos obrigatoriamente se juntam e se movem unidos com a mesma velocidade. Lembre-se de que em qualquer tipo de choque a quantidade de movimento sempre se conserva.

Gráfico da velocidade em função do tempo para a colisão inelástica das figuras abaixo

Choque parcialmente elástico

 Nesse tipo de choque o sistema é dissipativo com a energia sendo parcialmente dissipada e o coeficiente de restituição está compreendido entre 0 e 1 (0 < e < 1). Como em qualquer tipo de choque a quantidade de movimento do sistema se conserva.

Gráficos de uma colisão parcialmente elástica

O que você deve saber, informações e dicas

Coeficiente de restituição (e) é definido pela relação:

O coeficiente de restituição (e) é uma grandeza adimensional (não tem unidade), por ser calculado pela razão entre duas grandezas de mesma espécie e 0 < e > 1.

Cálculo do módulo da velocidade relativa:

  velocidades em sentidos contrários: V_r = V_X + V_Y

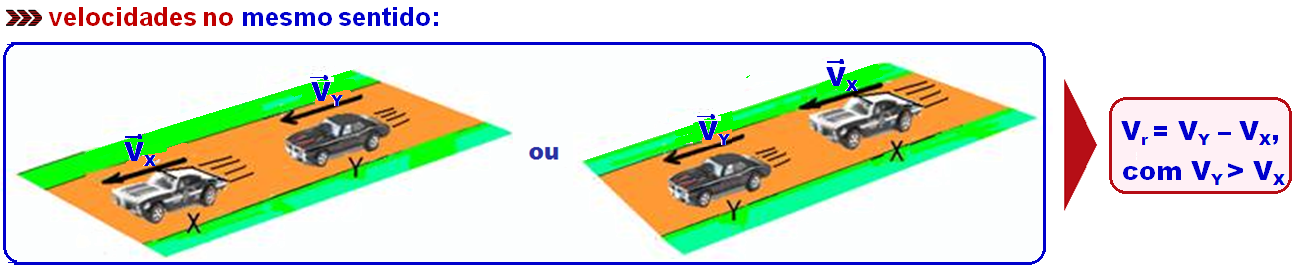
  velocidades no mesmo sentido: V_r = V_Y – V_X, com V_Y > V_X

O resultado V_r obtido é sempre em módulo.

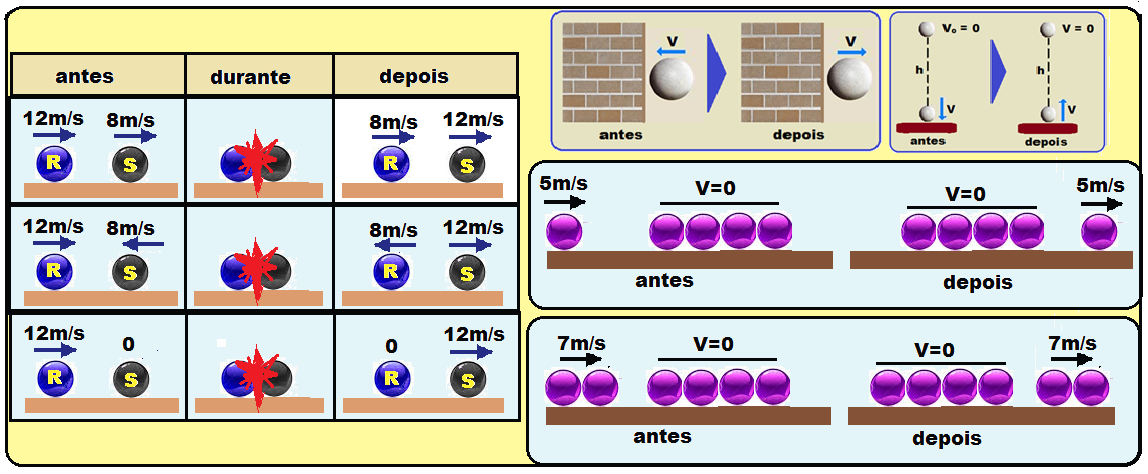
 Em todo choque perfeitamente elástico, se os corpos tiverem a mesma massa, eles trocam suas velocidades

Exemplos:

Exemplos de cálculo do valor do coeficiente de restituição e de classificação de tipos de choques:

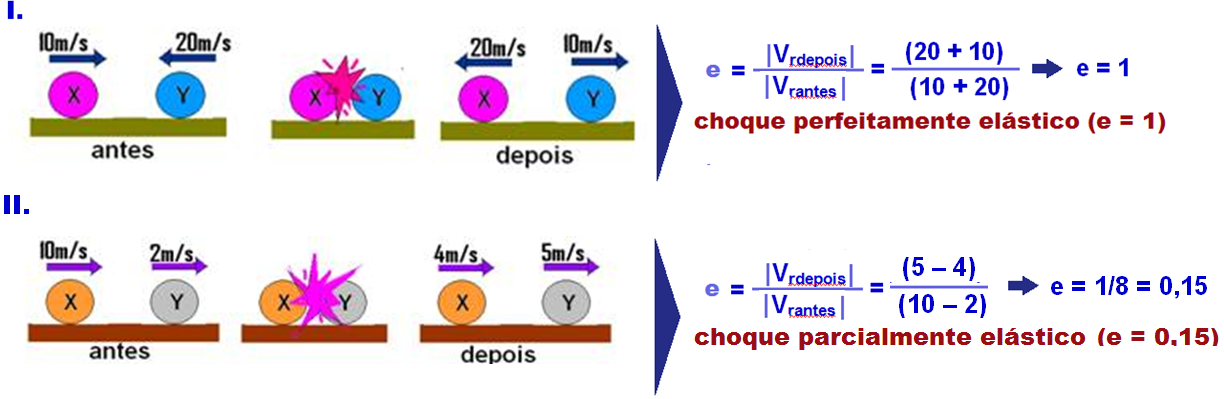
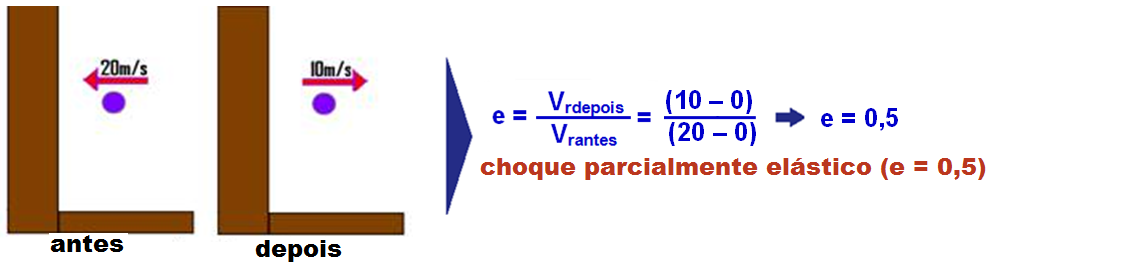
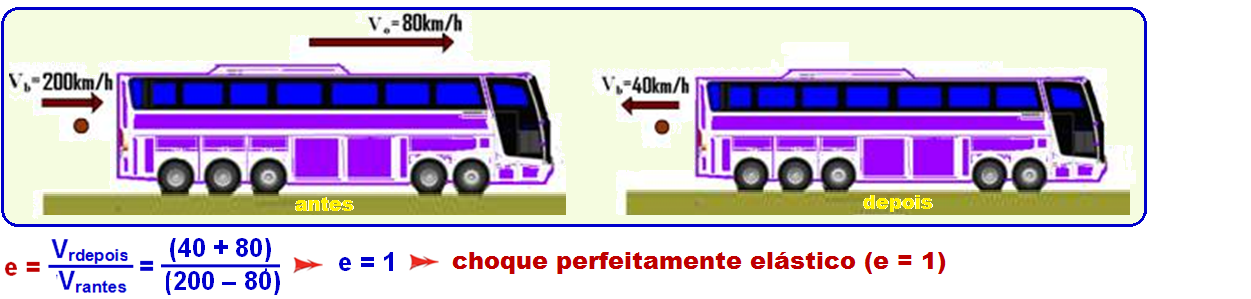
VI. Choque contra um obstáculo fixo (solo)

Esfera abandonada de uma altura H choca-se com o solo e retorna a uma altura h.

VII. Choque de uma pequena esfera (por exemplo, bola de tênis) contra um obstáculo móvel (por exemplo, um ônibus), com:

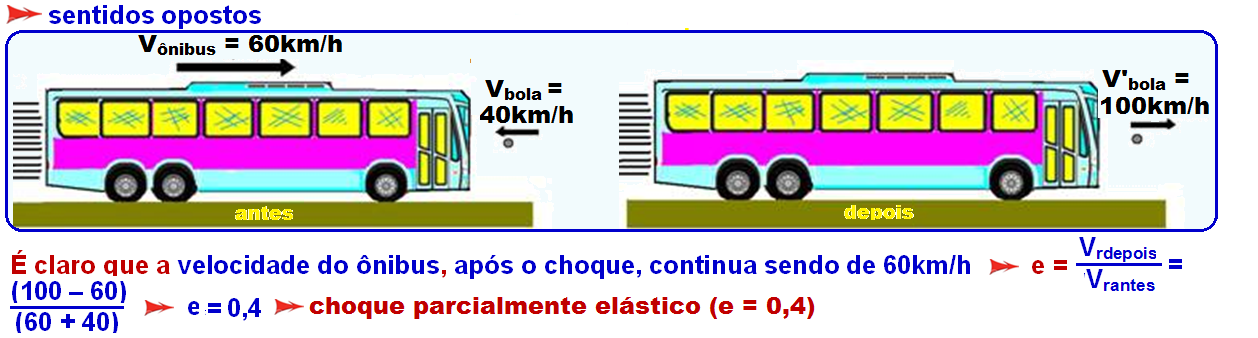
mesmo sentido

 VIII. Como resolver exercícios sobre colisões parcialmente elásticas ou colisões elásticas com massas diferentes:

Etapas

1^a fazer um desenho dos móveis antes e depois da colisão considerando, por exemplo, velocidades positivas para a direita e negativas para a esquerda

2^a calcular as quantidades de movimento do sistema antes e depois do choque, igualá-las e simplificá-las  equação I.

3^a utilizar o coeficiente de restituição e = módulo da velocidade relativa depois do choque/módulo da velocidade relativa antes do choque    e = V_rdepois/V_rantes, simplificar essa equação  equação II

4^a resolver o sistema formado pelas equações I e II

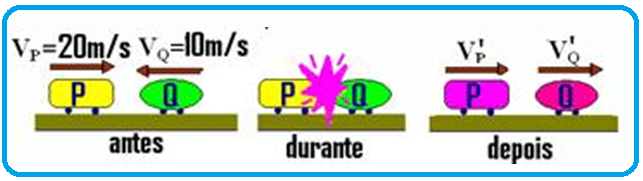
Exercício exemplo:

Dois móveis P e Q de massas m_P = 2kg e m_Q = 10kg se movem em sentidos contrários com velocidades V_P = 20m/s e V_Q = 10m/s e sofrem uma colisão unidimensional parcialmente elástica de coeficiente de restituição igual a 0,8. Calcule suas velocidades após o choque e seus sentidos.

Etapas:

1^a fazer um desenho dos móveis antes e depois da colisão considerando, por exemplo, que após a colisão os móveis se movam sempre para a direita.

2^a Calcular as quantidades de movimento do sistema antes e depois do choque, (supondo, por exemplo, velocidades positivas para a direita e negativas para a esquerda), igualá-las e simplificá-las.

Q_a = Q_d    m_PV_P + m_QV_Q=m_PV_P’ + m_QV_Q’    2.(20) + 10.(-10) = 2.V_P’ + 10.V_Q’   -60 = 2.V_P’ + 10.V_Q’     V_p’ + 5V_Q’= - 30  (equação I) 

3^a Utilizando o coeficiente de restituição e = 0,8   e = V_rdepois/V_rantes   0,8 = (V_Q’ – V_P’)/30  V_Q’ – V_P’ = 24 (equação II)  

4^a Resolvendo o sistema formado pelas equações I e II  isolando V’_Q em II   V’_Q = 24 – V’_P

III substituindo III em I V’_P + 5(24 + V’_P) = - 30 V’_P + 120 + 5V’_P = - 30 6V’_P = - 150

V’_P = - 25m/s (o móvel P, após o choque, se move para a esquerda com velocidade de 25m/s)

V_Q’ – V_P’ = 24 V_Q’ – (-25) = 24 V’_Q = - 1m/s (após o choque, o móvel Q também se move para a esquerda com velocidade de 1m/s) 

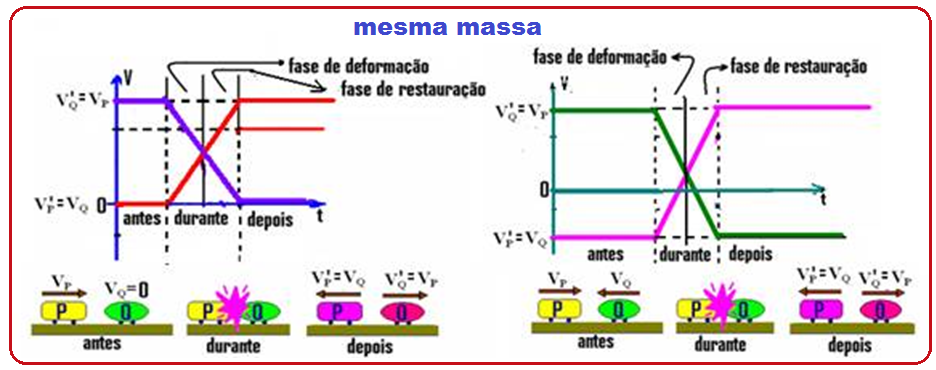
Caso particular de colisão perfeitamente elástica (e = 1) com os móveis possuindo mesma massa:

O procedimento é o mesmo que o do exercício anterior:

Exemplo: Dois carrinhos de brinquedo M e N que se movem em sentidos contrários sofrem uma colisão perfeitamente elástica. Suas velocidades antes do choque são V_M = 12m/s e V_N = 8m/s. Sua massas são iguais (2kg). Determine a intensidade e o sentido de suas velocidades após o choque.

Esquematizando a situação e supondo que após o choque, eles se movam para a direita.

 Aplicando o teorema da conservação da quantidade de movimento, supondo velocidades positivas para a direita e negativas para a esquerda    Q_a = Q_d    m_N.V_N + m_M.V_M = m_N.V_N’ + m_M.V_M’    2.(-8) + 2.(12) = 2.V_N’ + 2.V_M’    -16 +24 = 2.V_N’ + 2.V_M’   V_N’ + V_M’=4 I   

Aplicando a expressão do coeficiente de restituição e = V_rdepois/V_rantes   1 = (V_N’ – V_M’)/(12 + 8)    V_N’ – V_M’= 20 II 

Resolvendo o sistema composto por I e II    V_N’=12m/s (para a direita) e V_M’= - 8m/s (para a esquerda).

Observe que, após o choque, M transferiu a N sua velocidade de 12m/s para a direita e que N transferiu a M sua velocidade de 8m/s para a esquerda. Assim, pode-se concluir que:

“Em todo choque perfeitamente elástico, se os corpos tiverem a mesma massa eles obrigatoriamente trocam suas velocidades”

Exercícios de vestibulares com resolução comentada sobre

Colisões mecânicas

01-(EFB) Calcular, em cada caso, o que é pedido, considerando:

V_X – velocidade de X antes do choque  ---  V’_X – velocidade de  X depois do choque

V_Y – velocidade de Y antes do choque  ---  V’_Y – velocidade de Y depois do choque

e – coeficiente de restituição

a) Choque perfeitamente elástico – V’_Y=?

b) Calcular o coeficiente de restituição (e) e especificar o tipo de choque

c) Choque parcialmente elástico com coeficiente de restituição e=0,8 – V’_X=?

d) Choque parcialmente elástico com e=0,6 – V’_X=?

e) Calcular o valor do coeficiente de restituição e especificar o tipo de choque

f) Calcule o coeficiente de restituição e especifique o tipo de choque

02-(UNIFESP-SP) Completamente lotado, certo ônibus trafega a uma velocidade de 10 m/s. Um rapaz à beira da estrada brinca com uma bola de tênis. Quando o ônibus passa, ele resolve jogar a bola na traseira do mesmo. Sabendo-se que a bola atinge a traseira do ônibus perpendicularmente, com velocidade de 20 m/s, em relação ao solo, qual a velocidade horizontal final da bola após o choque ?

Considere o choque perfeitamente elástico.

Choque inelástico

03-(UNESP-SP) Um bloco A, deslocando-se com velocidade v_A em movimento retilíneo uniforme, colide frontalmente com um bloco B, inicialmente em repouso. Imediatamente após a colisão, ambos passam a se locomover unidos, na mesma direção em que se locomovia o bloco A antes da colisão. Baseado nestas informações e considerando que os blocos possuem massas iguais, é correto afirmar que:

a) a velocidade dos blocos após a colisão é v_A/2 e houve conservação de quantidade de movimento e de energia.

b) a velocidade dos blocos após a colisão é v_A e houve conservação de quantidade de movimento e de energia.

c) a velocidade dos blocos após a colisão é v_A e houve apenas conservação de energia.

d) a velocidade dos blocos após a colisão é v_A/2 e houve apenas conservação de quantidade de movimento.

e) a velocidade dos blocos após a colisão é v_A/2 e houve apenas conservação de energia.

 04-(PUC-MG) Um automóvel a 30m/s choca-se contra a traseira de outro de igual massa  que segue no mesmo sentido a 20m/s. Se os dois ficam unidos, a velocidade comum imediatamente após a colisão será, em m/s, de:

05-(UNICAMP-SP) Um objeto de massa m₁=4,0kg e velocidade V₁=3,0m/s choca-se com outro objeto em repouso, de massa m₂=2,0kg.. A colisão ocorre de maneira que a perda de energia cinética é máxima, mas consistente  com o Princípio de Conservação da Quantidade de Movimento.

a) Quais as velocidades dos objetos imediatamente após a colisão?

b) Qual a variação de energia cinética do sistema?

06-(UFPI) Na figura a seguir, o peixe maior, de massa M=5,0kg, nada para a direita a uma velocidade v=1,0m/s e o peixe menor, de massa m=1,0kg, se aproxima dele a uma velocidade U=8,0m/s, para a esquerda.

Despreze qualquer efeito de resistência da água. Após engolir o peixe menor, o peixe maior terá uma velocidade de:

a) 0,5m/s, para a esquerda     

b) 1,0m/s, para a esquerda     

c) nula     

d) 0,5m/s, para a direita     

e) 1,0m/s, para a direita

07-(Ufrrj-RJ) Eduardo, de massa igual a 30 kg, está parado, em pé sobre seu carrinho de 10 kg, quando seu cachorro Zidane, de 20 kg de massa, vem correndo e pula sobre o mesmo. Sabendo que o carrinho com Eduardo e Zidane passa a ter uma velocidade de 0,5 m/s, determine a velocidade do cachorro antes de ser apanhado pelo dono, considerando-a na direção horizontal.

08-(EFB) O gráfico abaixo, representa as velocidades de dois móveis X e Y em função do tempo, antes e depois de uma colisão. Calcule a massa do móvel Y, considerando a massa do móvel X como m_X=2kg.

09-(UFU-MG) Um garoto brinca com seu barquinho de papel, que tem uma massa igual a 30 g e está navegando sobre um pequeno lago. Em certo instante, ele coloca sobre o barquinho, sem tocá-lo, uma bolinha de isopor e percebe que o barquinho passa a andar com metade de sua velocidade inicial. Seu irmão mais velho, que observa a brincadeira, resolve estimar a massa da bolinha de isopor com base na variação da velocidade do barquinho. Desprezando efeitos relativos ao empuxo, ele conclui que a massa da bolinha é de

10-(UNICAMP-SP) O chamado "pára-choque alicate" foi projetado e desenvolvido na Unicamp com o objetivo de minimizar alguns problemas com acidentes. No caso de uma colisão de um carro contra a traseira de um caminhão, a malha de aço de um pára-choque alicate instalado no caminhão prende o carro e o ergue do chão pela plataforma, evitando, assim, o chamado "efeito guilhotina".

 Imagine a seguinte situação: um caminhão de 6000kg está a 54 km/h e o automóvel que o segue, de massa igual a 2000kg, está a 72 km/h. O automóvel colide contra a malha, subindo na rampa. Após o impacto, os veículos permanecem engatados um ao outro.

a) Qual a velocidade dos veículos imediatamente após o impacto?

b) Qual a fração da energia cinética inicial do automóvel que foi transformada em energia gravitacional, sabendo-se que o centro de massa do mesmo subiu 50 cm?

11- (Uerj-RJ) Duas esferas, A e B, deslocam-se sobre uma mesa conforme mostra a figura 1.

Quando as esferas A e B atingem velocidades de 8 m/s e 1 m/s, respectivamente, ocorre uma colisão perfeitamente inelástica entre ambas.

O gráfico na figura 2 relaciona o momento linear Q, em kg × m/s, e a velocidade , em m/s, de cada esfera antes da colisão.

Após a colisão, as esferas adquirem a velocidade, em m/s, equivalente a:

a

12-(UNIFESP-SP) A figura representa um pêndulo balístico usado em laboratórios didáticos.

A esfera disparada pelo lançador se encaixa em uma cavidade do bloco preso à haste - em conseqüência ambos sobem até ficarem presos por atrito em uma pequena rampa, o que permite medir o desnível vertical h do centro de massa do pêndulo (conjunto bloco-esfera) em relação ao seu nível inicial. Um aluno trabalha com um equipamento como esse, em que a massa da esfera é m_e = 10 g, a massa do bloco é m_b = 190 g e a massa da haste pode ser considerada desprezível. Em um ensaio experimental, o centro de massa do conjunto bloco-esfera sobe h = 10 cm.

a) Qual a energia potencial gravitacional adquirida pelo conjunto bloco-esfera em relação ao nível inicial?

b) Qual a velocidade da esfera ao atingir o bloco? Suponha que a energia mecânica do conjunto bloco esfera se conserve durante o seu movimento e adote g = 10 m/s².

13-(UFBA) No dia 4 de julho de 2005, coincidindo com as comemorações da independência dos Estados Unidos da América, os meios de comunicação de todo o mundo divulgaram o impacto de uma pequena nave, não tripulada, com o cometa Tempel 1. Uma animação do evento foi distribuída às emissoras de televisão e disponibilizada na rede de computadores. Alguns instantâneos dessa animação - apresentados nas figuras I, II e III - mostram respectivamente a nave ao encaminhar-se para o cometa, o instante da colisão e a cratera formada.

No dia seguinte, a imprensa internacional também divulgou que uma astróloga russa entrou com uma ação indenizatória na Justiça americana por perdas e danos. Alegava a referida senhora que a ação americana prejudicou a confiabilidade de seus mapas astrais, no momento em que modificou as condições de movimento de um corpo celeste.

Considere as informações:

- o choque foi frontal e completamente inelástico;

- o cometa, no referencial da nave, movia-se em sua direção com velocidade v(cometa) = 10km/s;

- o cometa, em forma de um paralelepípedo de dimensões 5km × 5km × 10km, tem densidade aproximadamente igual à densidade da água, d(água) = 1kg/litro;

- a nave, com massa igual a 100kg, não transportava explosivos.

Calcule a modificação na velocidade do cometa e faça um comentário sobre a alegação da astróloga russa.

14-(UFMG-MG) Em julho de 1994, um grande cometa denominado Shoemaker-Levi 9 atingiu Júpiter, em uma colisão frontal e inelástica.

De uma nave no espaço, em repouso em relação ao planeta, observou-se que a velocidade do cometa era de 6,0.10⁴m/s antes da colisão.

Considere que a massa do cometa é 3,0 × 10¹⁴ kg e que a massa de Júpiter é 1,8 × 10²⁷kg.

Com base nessas informações, CALCULE

a) a velocidade, em relação à nave, com que Júpiter se deslocou no espaço, após a colisão.

b) a energia mecânica total dissipada na colisão do cometa com Júpiter.

15- (MACKENZIE-SP) De um ponto situado a 12m acima do solo abandona-se uma bola, a qual, após chocar-se com o solo, alcança a altura de 6m. Determine o valor do coeficiente de restituição desse choque.

16-(IME-RJ) O carro A foi abalroado pelo caminhão B de massa igual ao triplo da massa do carro. O caminhão desloca-se com velocidade de 36 km/h. Após o choque, que se deu no ponto P, os dois veículos, unidos, deslocaram-se em linha reta até o ponto Q. O motorista do carro declarou que sua velocidade no instante do choque era inferior à máxima permitida, que é de 80km/h.

Diga, justificando, se essa declaração é falsa ou verdadeira.

17-(Ufrs-RS) Uma pistola dispara um projétil contra um saco de areia que se encontra em repouso, suspenso a uma estrutura que o deixa plenamente livre para se mover. O projétil fica alojado na areia. Logo após o impacto, o sistema formado pelo saco de areia e o projétil move-se na mesma direção do disparo com velocidade de módulo igual a 0,25 m/s. Sabe-se que a relação entre as massas do projétil e do saco de areia é de 1/999.

Qual é o módulo da velocidade com que o projétil atingiu o alvo?

18-(FUVEST-SP) Perto de uma esquina, um pipoqueiro, P, e um "dogueiro", D, empurram distraidamente seus carrinhos, com a mesma velocidade (em módulo), sendo que o carrinho do "dogueiro" tem o triplo da massa do carrinho do pipoqueiro. Na esquina, eles colidem (em O) e os carrinhos se engancham, em um choque totalmente inelástico.

Uma trajetória possível dos dois carrinhos, após a colisão, é compatível com a indicada por

Choque parcialmente elástico

19-(EFB) Dois móveis M e N movendo-se em sentidos opostos com velocidades de 5m/s e 3m/s respectivamente, sofrem uma colisão unidimensional, parcialmente elástica de coeficiente de restituição e=3/4. Suas massas são m_M=15kg e m_N=13kg. Determine a intensidade e o sentido de suas velocidades após o choque.

20-(UFRJ)

A esfera A, com velocidade 6,0m/s, colide com a esfera B, em repouso, como mostra a figura anterior. Após a colisão as esferas se movimentam com a mesma direção e sentido, passando a ser a velocidade da esfera A 4,0m/s e a da esfera B, 6,0m/s. Considerando m_Aa massa da esfera A e m_B a massa da esfera B, assinale a razão m_A/m_B e o coeficiente de restituição do choque:

21-(Ufrj-RJ) A figura representa o gráfico velocidade-tempo de uma colisão unidimensional entre dois carrinhos  A e B.

a) Qual é o módulo da razão entre a força média que o carrinho A exerce sobre o carrinho B e a força média que o carrinho B exerce sobre o carrinho A? Justifique sua resposta.

b) Calcule a razão entre as massa m_A e m_B dos carrinhos.

c) Calcule o valor do coeficiente de restituição

22-(UNESP) A figura mostra o gráfico das velocidades de dois carrinhos que se movem sem atrito sobre um mesmo par de trilhos horizontais e retilíneos. Em torno do instante 3 segundos, os carrinhos colidem.

Se as massas dos carrinhos 1 e 2 são, respectivamente, m₁ e m₂, então

a) m₁ = 3m₂.                 

b) 3m₁ = m₂.                   

c) 3m₁ = 5m₂.                 

d) 3m₁ = 7m₂.                 

e) 5m₁ = 3m₂.

23- (FUVEST-SP)Dois discos, A e B, de mesma massa M, deslocam-se com velocidades V_A= V_o e V_B = 2V_o, como na figura, vindo a chocar-se um contra o outro.

 Após o choque, que não é elástico, o disco B permanece parado. Sendo E_i a energia cinética total inicial (Ei = 5 x (1/2 MV_o/2)), a energia cinética total E_f, após o choque, e o coeficiente de restituição valem, respectivamente:

a) E_f= E_i e e=0,5                   

b) E_f = 0,8 E_i e e=0,8                  

c) E_f = 0,4 E_i e e=1                 

d) E_f = 0,2 E_i e e=1/3                   

e) E_f = 0 e e=0

24-(FUVEST-SP)

Em uma canaleta circular, plana e horizontal, podem deslizar duas pequenas bolas A e B, com massas M_A = 3 M_B, que são lançadas uma contra a outra, com igual velocidade V_o, a partir das posições indicadas. Após o primeiro choque entre elas (em 1), que não é elástico, as duas passam a movimentar-se no sentido horário, sendo que a bola B mantém o módulo de sua velocidade V_o. Pode-se concluir que o próximo choque entre elas ocorrerá nas vizinhanças da posição

25-(UFB) Por transportar uma carga extremamente pesada, um certo caminhão trafega a uma velocidade de 10 m/s. Um rapaz à beira da estrada brinca com uma bola de tênis. Quando o caminhão passa, ele resolve jogar a bola na traseira do mesmo. Sabendo-se que a bola atinge a traseira do caminhão perpendicularmente, com velocidade de 20 m/s, em relação ao solo, qual a velocidade horizontal final da bola após o choque ?

Considere um choque parcialmente elástico de coeficiente de restituição e=0,6

Choque perfeitamente elástico

26- Fuvest-SP) Dois caixotes de mesma altura e mesma massa, A e B, podem movimentar-se sobre uma superfície plana, sem atrito. Estando inicialmente A parado, próximo a uma parede, o caixote B aproxima-se perpendicularmente à parede, com velocidade V_o, provocando uma sucessão de colisões elásticas no plano da figura.

Após todas as colisões, é possível afirmar que os módulos das velocidades dos dois blocos serão aproximadamente:

a) V_A = V_o e V_B = 0.         

b) V_A = V_o/2 e V_B = 2 V_o.         

c) V_A = 0 e V_B = 2 V_o.         

d) V_A = V_o/√2 e V_B = V_o/√2 
e) V_A = 0 e V_B = V_o.

27-(UFRJ) A figura mostra uma mesa de bilhar sobre a qual se encontram duas bolas de mesma massa. A bola (1) é lançada em linha reta com uma velocidade v_o e vai se chocar frontalmente com a bola (2), que se encontra em repouso.

Considere o choque perfeitamente elástico e despreze os atritos.

Calcule, em função de v_o, as velocidades que as bolas (1) e (2) adquirem após o choque.

28-(MACKENZIE-SP) A esfera A, de massa 2 kg e velocidade 10 m/s, colide com outra B de 1 kg, que se encontra inicialmente em repouso. Em seguida, B colide com a parede P. Os choques entre as esferas e entre a esfera B e a parede P são perfeitamente elásticos. Despreze os atritos e o tempo de contato nos choques. A distância percorrida pela esfera A entre o primeiro e o segundo choque com a esfera B é:

29-(Ufms-MS) Considere um choque elástico unidimensional entre um corpo A, em movimento, que está se aproximando de um corpo B, inicialmente em repouso, ambos esféricos. Assinale a(s) alternativa(s) correta(s).

(01) Se a massa dos corpos A e B for igual, a velocidade dos corpos, após o choque, será igual.

(02) Se a massa do corpo B for metade da massa do corpo A, a velocidade dos corpos A e B, após o choque, será igual, mas terá a metade do valor da velocidade do corpo A antes do choque.

(04) Se a massa dos corpos A e B for igual, após o choque, a velocidade do corpo B será igual à do corpo A antes do choque e a velocidade do corpo A será nula.

(08) Se a massa dos corpos A e B for igual, a quantidade de movimento de cada corpo, após o choque, será igual à metade do valor da quantidade de movimento do corpo A antes do choque.

(16) Se a massa do corpo B for o dobro da massa do corpo A, após o choque, a velocidade do corpo A terá sentido oposto ao da sua velocidade antes do choque.

30-(Olimpíada Brasileira de Física) São realizadas experiências com 5 pêndulos de mesmos comprimentos. As massas pendulares são de bolas de bilhar iguais, cada uma ligeiramente encostada na outra.

Experiência 1: A bola 1 é erguida de uma altura H e abandonada. Ela colide com a bola 2. O choque se propaga e a bola 5 é lançada, praticamente até a mesma altura H.

Experiência 2: Agora as bolas 1 e 2 são erguidas conforme ilustra a figura e abandonadas. Elas caminham juntas até a colisão com a bola 3.

Dois estudantes, Mário e Pedro, têm respostas diferentes com relação à previsão do que irá ocorrer após a propagação do choque. Mário acha que somente a bola 5 irá se movimentar, saindo com velocidade duas vezes maior que as velocidades das bolas 1 e 2 incidentes. Pedro acha que as bolas 4 e 5 sairão juntas com a mesma velocidade das bolas incidentes 1 e 2.

a) A previsão de Mário é correta? Justifique.         

b) A previsão de Pedro é correta? Justifique.

31-(Ufpe) Um pequeno bloco, de massa m = 0,5 kg, inicialmente em repouso no ponto A, é largado de uma altura h = 0,8 m. O bloco desliza ao longo de uma superfície sem atrito e colide com um outro bloco, de mesma massa, inicialmente em repouso no ponto B (veja a figura a seguir).

 Determine a velocidade do segundo bloco após a colisão, em m/s, considerando-a perfeitamente elástica.

32-(FUVEST-SP) Duas pequenas esferas iguais, A e B, de mesma massa, estão em repouso em uma superfície horizontal, como representado no esquema a seguir. No instante t = 0 s, a esfera A é lançada, com velocidade V_o = 2,0 m/s, contra a esfera B, fazendo com que B suba a rampa à frente, atingindo sua altura máxima, H, em t = 2,0 s.

Ao descer, a esfera B volta a colidir com A, que bate na parede e, em seguida, colide novamente com B. Assim, as duas esferas passam a fazer um movimento de vai e vem, que se repete.

a) Determine o instante t_A, em s, no qual ocorre a primeira colisão entre A e B.

b) Represente, no gráfico a seguir, a velocidade da esfera B em função do tempo, de forma a incluir na representação um período completo de seu movimento.

c) Determine o período T, em s, de um ciclo do movimento das esferas.

NOTE E ADOTE:

Os choques são elásticos. Tanto o atrito entre as esferas e o chão quanto os efeitos de rotação devem ser desconsiderados.

Considere positivas as velocidades para a direita e negativa as velocidades para a esquerda.

33-(UNIFESP-SP) A figura mostra a situação anterior a um choque elástico de três bolas idênticas. A bola 1 tem velocidade ; as bolas 2 e 3 estão em repouso (figura 1). Depois do choque, as bolas passam a ter velocidades ,‚ e .

A alternativa que representa uma situação possível para o movimento dessas bolas depois do choque é:

34-(FUVEST-SP) Dois pequenos discos, de massas iguais são lançados sobre uma superfície plana e horizontal, sem atrito, com velocidades de módulos iguais. A figura a seguir registra a posição dos discos, vistos de cima, em intervalos de tempo sucessivos e iguais, antes de colidirem, próximo ao ponto P.

Dentre as possibilidades representadas, aquela que pode corresponder às posições dos discos, em instantes sucessivos, após a colisão é:

35-(UNESP-SP) Na figura, P e Q são blocos idênticos que se comportam numa colisão como corpos perfeitamente elásticos. Sobre o bloco P, no percurso ao longo do trecho horizontal AB, atua uma força de atrito constante de módulo igual a 10N. Não há atrito no trecho BC. Os corpos P e Q tem massa igual a 5,0kg, g=10m/s². Considerar os blocos como pontos materiais. A velocidade do bloco P no ponto A é v=10m/s.

O ponto mais alto atingido pelo bloco Q ao percorrer o trecho BC é:

36-(CFT-MG) Um disco de massa M_A desloca-se sobre uma superfície horizontal, sem atrito, com velocidade V_A e atinge frontalmente um outro disco de massa M_B, em repouso, em uma colisão perfeitamente elástica.

As velocidades dos discos, após essa colisão, podem ser determinadas, ao se considerar a

a) energia cinética antes e depois do choque de ambos. 

b) conservação da energia cinética e da quantidade de movimento dos discos. 

c) conservação de energia cinética e da quantidade de movimento de um dos discos. 

d) quantidade de movimento antes e depois do choque de cada corpo isoladamente. 

37-(UFF-RJ)  Duas bolas de mesma massa, uma feita de borracha e a outra feita de massa de modelar, são largadas de uma mesma altura. A bola de borracha bate no solo e retorna a uma fração da sua altura inicial, enquanto a bola feita de massa de

modelar bate e fica grudada no solo. Assinale a opção que descreve as relações entre as intensidades dos impulsos Ib e Im exercidos, respectivamente, pelas bolas de borracha e de massa de modelar sobre o solo, e entre as respectivas variações de energias cinéticas ΔEbc e ΔEmc das bolas de borracha e de massa de modelar devido às colisões.

a) Ib < Im e ΔEbc  > ΔEmc        

b) Ib < Im e ΔEbc  < ΔEmc        

c) Ib > Im e ΔEbc  > ΔEmc        

d) Ib > Im e ΔEbc  < ΔEmc 

e) Ib = Im e ΔEbc  < ΔEmc 

38-(PUC-SP)  Nas grandes cidades é muito comum a colisão entre veículos nos cruzamentos de ruas e avenidas.

Considere uma colisão inelástica entre dois veículos, ocorrida num cruzamento de duas avenidas largas e perpendiculares. Calcule a velocidade dos veículos, em m/s, após a colisão.

Considere os seguintes dados dos veículos antes da colisão:

Veículo 1  ---   m₁= 800kg  ---  v₁= 90km/h  ---  Veículo 2  ---   m₂ =450kg  ---  v₂= 120km/h

39-(UPE-PE)  O esquema a seguir mostra o movimento de dois corpos antes e depois do choque. Considere que o coeficiente

de restituição é igual a 0,6. Analise as proposições a seguir e conclua.

(     )  A velocidade do corpo B após o choque é 18 m/s.

(     )  A massa do corpo A vale 2 kg.

(     )  O choque é perfeitamente elástico, pois os dois corpos têm massas iguais a 2 kg

(     )  A quantidade de movimento depois do choque é menor do que antes do choque.

(     )  A energia dissipada, igual à diferença da energia cinética antes do choque e da energia cinética depois do choque, é de 64 J.

40-(UFSM-RS) O estresse pode fazer com que o cérebro funcione aquém de sua capacidade. Atividades esportivas ou atividades lúdicas podem ajudar o cérebro a normalizar suas funções.

Num certo esporte, corpos cilíndricos idênticos, com massa de 4kg, deslizam sem atrito sobre uma superfície plana. Numa jogada,

um corpo A movimenta-se sobre uma linha reta, considerada o eixo x do referencial, com velocidade de módulo 2m/s e colide com outro corpo, B, em repouso sobre a mesma reta. Por efeito da colisão, o corpo A permanece em repouso,

e o corpo B passa a se movimentar sobre a reta. A energia cinética do corpo B, em J, é

41-(UFJF-MG) A figura ao lado mostra um sistema composto por dois blocos de massas idênticas m_A=m_B=3,0kg  e 4,0 N / m. O bloco A está preso a um fio de massa desprezível e suspenso de

umauma mola de constante elástica k=3,0 m e que a colisão entre os blocos A e B é elástica, faça o que se pede nos itens seguintes.0,8 m em relação à superfície S , onde está posicionado o bloco B . Sabendo que a distância entre o bloco B e a mola é d =altura h=

a) Usando a lei de conservação da quantidade de movimento (momento linear), calcule a velocidade do bloco B imediatamente após a colisão do bloco A .

b) Calcule o deslocamento máximo sofrido pela mola se o atrito entre o bloco B e o solo for desprezível.

c) Calcule a distância deslocada pelo bloco B em direção à mola, se o atrito cinético entre o bloco B e o solo for igual  a μ=0,4. Nesse caso, a mola será comprimida pelo bloco B ? Justifique.

42-(UEPB-PB) Um garoto brincando de bola de gude com seu colega executou uma jogada e percebeu que, ao lançar sua bola A,

 com certa velocidade V_A contra a bola B de seu colega, a qual se encontrava em repouso, o seguinte fenômeno aconteceu

imediatamente após a colisão entre as bolas: a bola A ficou parada, enquanto a bola B adquiriu uma velocidade igual a V_A (velocidade da bola A), antes da colisão. Esta situação pode ser representada através da figura acima, sendo I, a

situação antes das bolas colidirem e II a situação após a colisão.

Considerando que esta observação só seria possível num plano horizontal e sem atrito, é correto afirmar que

a) a colisão mostrada é inelástica.                                                

B) a energia cinética não se conservou.

c) a massa da bola A é maior que a massa da bola B.                  

d) a quantidade de movimento se conservou.

e) a quantidade de movimento não se conservou.

43-(UPE-PE) Na figura a seguir, observa-se que o bloco A de massa m_A = 2,0 kg, com velocidade de 5,0 m/s, colide com

um segundo bloco B de massa m_B = 8,0kg, inicialmente em repouso. Após a colisão, os blocos A e B ficam grudados e sobem juntos, numa rampa até uma altura máxima h em relação ao solo. Despreze os atritos e a assinale, na coluna I, as afirmativas verdadeiras e, na coluna II, as falsas.

44-(CEFET-MG) Se dois corpos sofrem uma colisão perfeitamente inelástica, então, a energia mecânica ______ , a energia cinética ________ e o momento linear _________ .

Os termos que completam, correta e respectivamente, as lacunas são:

a) varia, varia, varia.                               

b) varia, varia, conserva-se.                         

c) conserva-se, conserva-se, varia.

d) varia, conserva-se, conserva-se.         

e) conserva-se, conserva-se, conserva-se.

45-(FUVEST-SP)

Uma pequena bola de borracha maciça é solta do repouso de uma altura de 1 m em relação a um piso liso e sólido. A colisão da bola com o piso tem coeficiente de restituição ε=0,8. A altura máxima atingida pela bola, depois da sua terceira colisão com o piso, é

46-(UNICAMP-SP)

 O tempo de viagem de qualquer entrada da Unicamp até a região central do campus é de apenas alguns minutos. Assim,  a

economia de tempo obtida, desrespeitando-se o limite de velocidade, é  muito pequena, enquanto o risco de acidentes aumenta significativamente.

a)  Considere que um ônibus de massa M = 9000 kg , viajando a 80 km/h,  colide  na traseira de um carro de massa  m_a=1000 kg

que se encontrava parado. A colisão é  inelástica, ou seja, carro e ônibus seguem grudados após a batida.  Calcule a  velocidade do conjunto logo após a colisão.

b)  Além do excesso de velocidade, a falta de manutenção do veículo pode causar acidentes. Por exemplo, o  desalinhamento das rodas faz com que o carro sofra a ação de uma força lateral. Considere um carro com um pneu dianteiro desalinhado de 3°, conforme  a figura abaixo, gerando uma componente lateral da força de atrito   em uma das rodas. 

Para um carro de massa  m_b=1600 kg, calcule o módulo da aceleração lateral do carro, sabendo que o módulo da força de atrito em cada roda vale F_at= 8000 N . Dados: sen 3° = 0,05 e cos 3° = 0,99.

47-(UNIFESP-SP)

Um corpo esférico, pequeno e de massa 0,1 kg, sujeito a aceleração gravitacional de 10 m/s², é solto na borda de uma pista que

tem a forma de uma depressão hemisférica, de atrito desprezível e de raio 20 cm, conforme apresentado na figura.

Na parte mais baixa da pista, o corpo sofre uma colisão frontal com outro corpo, idêntico e em repouso. Considerando que a colisão relatada seja totalmente inelástica, determine:

a) O módulo da velocidade dos corpos, em m/s, imediatamente após a colisão.

b) A intensidade da força de reação, em newtons, que a pista exerce sobre os corpos unidos no instante em que, após a colisão, atingem a altura máxima.

48-(AFA)

 De acordo com a figura abaixo, a partícula A, ao ser abandonada de uma altura H, desce a rampa sem atritos ou resistência do ar até

sofrer uma colisão, perfeitamente elástica, com a partícula B que possui o dobro da massa de A e que se encontra inicialmente em

repouso. Após essa colisão, B entra em movimento e A retorna, subindo a rampa e atingindo uma altura igual a: (g=10m/s²).

Resolução comentada dos exercícios de vestibulares sobre

Colisões Mecânicas

01-

a) e=V_rdepois/V_rantes  ---  1=(10 + V’_Y)/(5 + 10)  ---  15=10 +V’_y  ---  V’_y=5m/s

b) e=V_rdepois/V_rantes=(4 – 2)/(5 – 1)  ---  e=0,5 (choque parcialmente elástico)

c) 0.8=V’_X/15  ---  V’_X=8m/s

d) 0,6=(V’_X – 40)/(40 + 60)  ---  60=V’_X – 40  ---  V’_X=100 km/h

e) e=0/4  ---  e=0 (choque inelástico)

f) e=√4/16  ---  e=0,25 (choque parcialmente elástico)

02- Considere o choque perfeitamente elástico.

e=V_rdepois/V_rantes  ---  1=(V’_b + 10)/(20 – 10)  ---  10=V’_b + 10  ---  V’_b=0

03- m_A=m_B=m  ---   Q_a=m_AV_A + m_BV_B=mV_A + 0  ---  Q_a=mV_A  ---  Q_d=(m_A + m_B)V’=2mV’ ---  Q_d=2mV’  --- Q_a=Q_d  ---  mV_A=2mV’  ---  V’=V_A/2 – R- D

04- Considerando as velocidades para a direita como positivas:

Antes  ---  Q_a=m30 + m.20=50.m ---  Q_a=50.m  ---  depois  ---  Q_d=mV’ + mV’=2mV’  ---  Q_a=Q_d  ---  50m=2mV’  ---  V’=25m/s

05- a) Como a perda de energia cinética é máxima, o choque é inelástico  ---  Q_a=m₁V₁ + m₂V₂=4.3 + 0  ---  Q_a=12kg.m/s  ---  Q_d=(m₁ + m₂₎.V’=(4 + 2).V’  ---  Q_d=6V’  ---  Q_a=Q_d  ---  12=6V’  ---  V’=2m/s

b) E_ca=m₁V₁²/2 + m₂V₂²/2=4.9/2 + 0  ---  E_ca=18J  ---  E_cd=m_1V’²/2 + m₂V’²/2=4.4/2 + 2.4/2  ---  E_cd=12J  ---  ΔE_c=18 – 12 = 6j

06- Considerando velocidade4s positivas para a direita  ---  Q_a=5.1 + 1.(-8)  ---  Q_a= -3kg.m/s  ---  Q_d=(5 + 1)V’  ---  Q_d=6V’  --- 

Q_a=Q_d  ---  - 3 =6V’  ---  V’= - 0,5m/s (negativa, para a esquerda) R- A

07- Estabelecendo velocidades para a esquerda como positivas  ---  Q_a=(30 + 10).0 + 20.V_Z  ---  Q_a=20V_Z  ---  Q_d=(30 + 10 +20).0,5 

---  Q_d=30kg.m/s  ---  Q_a=Q_d  ---  20V_z=30  ---  V_z=1,5m/s

08- Trata-se de um choque inelástico (e=0) e eles, após o choque, se movem juntos com velocidade comum de 8m/s  ---  Q_a=m_X.V_X + m_Y.V_Y=2.12 + m_Y.4  ---  Q_a=24 + 4.m_Y  ---  Q_d=(m_X + m_Y).V’=(2 + m_Y).8  ---  Q_d=16 + 8m_Y  ---  Q_a=Q_d  ---  24 + 4m_Y=16 + 8m_Y  ---  8=4m_Y  ---  m_Y=2kg

09-

Q_a=30V  ---  Q_d=(30 + m’).V/2  ---  Q_a=Q_d  ---  30V=(30 + m’).V/2   ---  60=30 + m’  --- m´=30g R- D ---  ou, o sistema deverá conservar a quantidade de movimento horizontal inicial. Desta forma como a velocidade foi reduzida à metade, a massa do sistema deverá dobrar, passando de 30 g para 60 g. A diferença de 30 g corresponde a bolinha de isopor. R- D

10- a) Considerando velocidades para a esquerda como positivas  ---  m_c=6.000kg – V_c=54km/h/3,6=15m/s  ---  m_a=2.000kg –

V_a=72km/h/3,6=20m/s  ---  Q_a=m_aV_a + m_cV_c=2.000.20 + 6.000.15  ---  Q_a=130.000kg.m/s  ---  Q_d=(m_c + m_a)V’=8.000V’  ---  Q_d=8.000V’  ---  Q_a=Q_d  ---  130.000=8.000V’  ---  V’=16,25m/s X 3,6   ---  V’=58,5 km/h

b) Energia cinética inicial do carro – E_ci=m_cV_c²/2=2.000.(20)²/2   ---  E_ci=400.000J  ---  Energia potencial gravitacional de centro de massa do carro que subiu h=50cm=0,5m  ---  E_p=m_a.g.h=2.000.10.0,5  ---  E_p=10.000J  ---  regra de três  ---  400.000J – 100%  ---  10.000J – p  ---   p=10/4  ---  p=2,5%

11- Q_A=m_AV_A  ---  80.10^-3=m_A.8  ---  m_A=80.10^-3/8  ---  m_A=10^-2kg  ---  Q_B=m_BV_B  ---  25.10^-3=m_B.1  ---  m_B=25.10^-3kg=2,5.10^-2kg  --- 

Q_a=m_AV_A + m_BV_B=10^-2.8 + 2,5.10^-2.1  ---  Q_A=10,5.10^-2kg.m/s  ---  Q_d=(m_A + m_B)V’=3,5.10^-2.V’  ---  Q_a=Q_d  ---  10,5.10^-2=3,5.10^-2.V’  ---  V’=3m/s  R- C

12- a)

 E_p=Mgh=(0,01 + 0,190).10.0,1  ---  E_p=0,2.10.0,1  ---  E_p=0,2J

b) Cálculo da velocidade (V_Q) com que o conjunto bloco esfera de massa M=0,2kg sai de Q e chega em P com velocidade nula  --- 

conservação da energia mecânica   ---  E_mP=E_mQ  ---  E_cP + E_pP=E_cQ + E_pQ  ---  0 + 0,2=MV_Q²/2 + 0  ---  0,2=0,2V_Q²/2  ---  V_Q=√2m/s  ---  choque inelástico da esfera de massa m= 0,01kg que chega com velocidade V_e com o bloco de massa m_b=0,190kg que está em repouso sendo que, após o choque o conjunto de massa M=0,2kg se move com V’=√2m/s  ---  

Q_a=0,01.V_e + 0  ---  Q_a=0,01V_e ---  Q_d=0,2V’=0,2.√2  ---  Q_a=Q_d  ---  0,01V_e=0,2.√2  ---  V_e=20.√2≈20.1,4  ---  V_e≈28m/s

13-

d_água=1kg/L=1kg/10^-3m³  ---  d_água=10³kg/m³  ---  V_c=5.10³.5.10³.10.10³  ---  V_c=25.1010m³  ---  d_água=M_c/V_c  ---  10³=M_c/25.10¹⁰  ---  M_c=25.10¹³kg  ---  M_n=100kg   ---  antes - V_c=10km/s  ---  V_n=0  ---  Q_a=M_cV_c + M_nV_n=25.10¹³.10 + 0  ---  Q_a=25.10¹⁴kg.m/s  choque inelástico – movem se juntos com velocidade V’  ---  Q_d=(M_c + M_n)V’=(25.10¹³ + 100)V’  ---  como 100kg é desprezível em relação a 25.10¹³kg  ---  Q_d=25.10¹³ V’  ---  Q_a=Q_d  ---  25.10¹⁴=25.10¹³ V’  ---  V’=10km/s (observe que a velocidade do cometa, após o choque com a nave praticamentenão sofreu alteração e a astróloga russa estava errada, pois essa alteração é muito pequena e não afeta o equilíbrio do Sistema Solar).

14- a)  Q_a=Q_d  ---  6.10⁴.3.10¹⁴ + 0 = (3.10¹⁴ + 1,8.10²⁷)V’  ---  observe que 3.10+14kg é praticamente desprezível em relação a 1,8.10²⁷kg  ---  18.10¹⁸=1,8.10²⁷V’  ---  V’=10^-8m/s (esse valor é desprezível e esse choque não afetou a velocidade de Júpiter)

b) A energia mecânica total dissipada foi toda energia cinética perdida pelo cometa no choque  --- E_dissipada=MV²/2=3.10¹⁴.(6.10⁴)²/2  ---  E_dissipada=5,4.10²³J

15- e=√6/12  ---  e=√2/2

16- m_ca=3m_c  ---  antes  --- Q_a=m_cV_c  ---  Q_ca=m_ca.V_ca=3m_ca.10   ---  Q_ca=30m_c  ---   (veja figura)  ---  aplicando

sen45^o=cateto oposto/hipotenusa  ---  sen45^o=Q_ca/Q_c  ---  √2/2=30m_c/m_cV_c  ---  V_c=60/√2 ≈60/1,4≈43m/s X 3,6 ≈145km/h – a declaração é falsa, pois a velocidade do carro era aproximadamente de 145km/h

17- m_p/m_s=1/999  ---  m_s=999m_p  ---  Q_a=Q_d  ---  m_pV_p+ 0=(m_p + m_s).0,25  ---  m_pV_p=(m_p + 999m_p).0,25  ---  m_pV_p=1.000m_p.0,25  --- 

V_p=250m/s R- C

18- Trata-se de um choque inelástico oblíquo (se movem juntos após o choque) 

R- B

19- Esquematizando a situação e supondo que após o choque, eles se movam para a direita

Aplicando o teorema da conservação da quantidade de movimento, supondo velocidades positivas para a direita e negativas para a esquerda  ---  Q_a=Q_d  ---  m_N.V_N + m_M.V_M = m_N.V_N’ + m_M.V_M’  ---  13.(-3) + 15.(5) = 13.V_N’ + 15.V_M’  ---  -39 +75 = 13.V_N’ + 15.V_M’  ---  13.V_N’ + 15.V_M’=36 I   ---  aplicando a expressão do coeficiente de restituição – e=V_rdepois/V_rantes  ---  3/4 = (V_N’ – V_M’)/(5 + 3)  ---  V_N’ – V_M’=6 II  ---  resolvendo o sistema composto por I e II  ---  V_N’=4,5m/s (para a direita) e V_M’= -1,5m/s (para a esquerda).

20- Esquematizando a situação

Q_a=Q_d  ---  m_A.6 + 0 = m_A.4 + m_B.6  ---  2m_A=6m_B  ---  m_A/m_B=3  ---  e=V_rd/V_ra=(6-4)/6  ---  e=1/3 R- C