Associação de molas

Duas molas 1 e 2 tem constantes elásticas k₁ e k₂, respectivamente. Podemos associá-las em série ou em paralelo. Em cada uma dessas associações podemos substituir as duas molas por uma única, que produza o mesmo efeito e que chamamos de mola equivalente de constante elástica k_e.

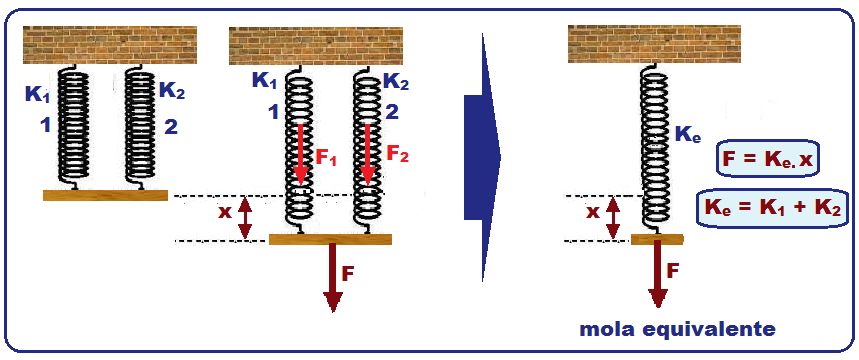
Associação em paralelo

Nesse caso a deformação x sofrida por cada uma das molas é a mesma.

Quando deformadas de x, a mola 1 fica sujeita a uma força F₁ = k₁.x e a mola 2 a uma força F₂ = k₂.x.

A mola equivalente, quando submetida à mesma força F, sofre a mesma deformação x de modo que F = k_e.x.

Observe que F = F₁ + F₂   k_e.x = k₁.x + k₂.x k_e = k₁ + k₂.

Se você tiver n molas   K_e = K₁ + K₂ + K₃ + .... K_n.

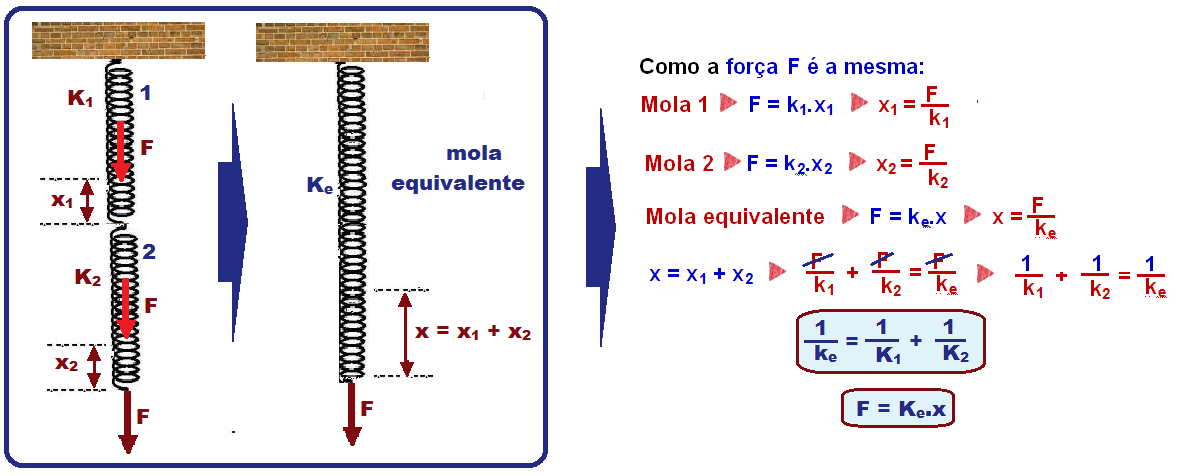
Associação em série

Nesse caso as molas 1 e 2 estão sujeitas à mesma força F e sofrem deformações diferentes x₁ e x_2.

Se você tiver n molas 1/K_e = 1/K₁ + 1/K₂ + 1/K₃ + .... 1/K_n.

O que você deve saber, informações e dicas

A constante elástica é algo que define a mola, isto é, suas características físicas (maleabilidade, maciez), constantes elásticas maiores tendem a ter uma rigidez maior.

Associação em série

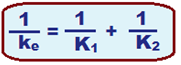
Associação em paralelo

Na associação de molas em série onde 1/k_e = 1/k₁ + 1/k₂, o valor de k_e fica bastante reduzido, sendo que a mola equivalente é menos rígida, mais deformável.

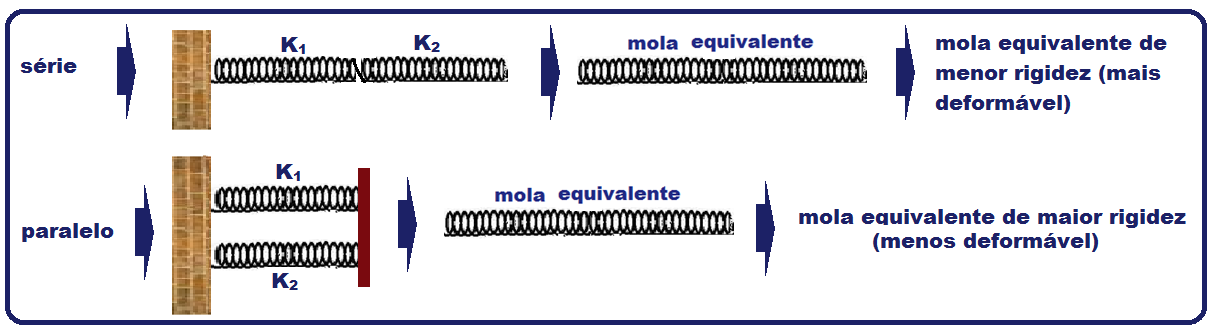
Se quisermos aumentar a rigidez da mola equivalente, torna-a menos deformável, devemos associar as molas em paralelo, onde k_e = k₁  + k₂. É mais eficaz e ocupa menos espaço.

 Você parte uma mola de constante elástica K em duas partes iguais, de modo a obter duas molas idênticas.

Cálculo da constante elástica K’ de cada pedaço que é diferente de K, pois apesar do material ser o mesmo, o número de espiras diminui:

A mola original de constante elástica K é composta das duas metades de constantes elásticas K’, associadas em série.

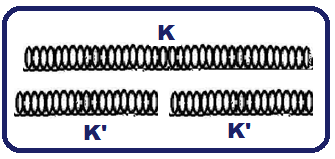
Na associação em série 1/K = 1/K’ + 1/K’ 1/K = 2/K’ K’ = 2K (a rigidez de cada metade fica o dobro da constante da mola original, tornando-as menos deformáveis).

Se você associar cada uma dessas metades de (K’ = 2K) em paralelo você obterá uma mola de

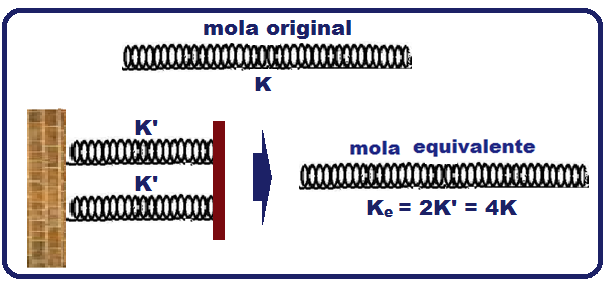
constante elástica equivalente K_e, tal que K_e = K’ + K’ = 2K + 2K K_e = 4K (a rigidez da mola equivalente da associação paralelo dessas duas metades fica quatro vezes maior que o da constante da mola original, tornando a mola equivalente menos deformável).

Exercícios de vestibulares com resolução comentada sobre

Associação de molas

01-(MACKENZIE-SP) Uma mola helicoidal de massa desprezível está presa pela extremidade A, a uma parede rígida e, na extremidade B, encontra-se preso um corpo de massa m, conforme mostra a figura 1. Quando o conjunto oscila livremente na direção da reta horizontal AB, perpendicular à parede, constitui-se um oscilador harmônico de período T. Se dispusermos de duas molas idênticas à anterior e as fixarmos conforme a figura 2, ao constituirmos um oscilador harmônico, com a oscilação do mesmo corpo de massa m, segundo a mesma direção AB, seu respectivo período será:

figura 1 

figura 2 

02-(UFB) Uma massa M=(20/9)kg, encontra-se suspensa ao conjunto de molas ilustrado na figura abaixo. Suas constantes elásticas são k₁ = k₂=30N/m.

a) A constante elástica total equivalente do conjunto.

b) A freqüência de oscilação do conjunto. (adote p =3)

03-(ITA-SP) Um sistema massa-molas é constituído por molas de constantes k₁ e k₂, respectivamente, barras de massas desprezíveis e um corpo de massa m, como mostrado na figura.

Determine a freqüência desse sistema.

04-(UFB) A mola helicoidal (figura 1), de constante elástica k=12N/m, foi partida em 3 partes iguais. Em seguida, essas 3 partes foram associadas em paralelo (figura 2) e em série (figura 3).    

figura 1

figura 2

figura 3

As massas das figuras 2 e 3 são iguais e valem 100g. Adote g=10m/s² e determine:

a) a constante elástica de cada parte.

b) o período de oscilação do conjunto quando as três molas estão associadas em paralelo.

c) o período de oscilação do conjunto quando as três molas estão associadas em série.

05-(PUC-SP) Na figura abaixo, as três molas ideais 1, 2 e 3 são idênticas  e possuem a mesma constante elástica de valor 0,1N/cm e as massas também são idênticas e de mesmo valor (10g).

Inicialmente, o conjunto está em equilíbrio e as molas estão em seu comprimento natural (20cm cada uma). Em seguida, retira-se o suporte S e cada mola se distende até que o conjunto adquira novamente o equilíbrio.

Após o novo equilíbrio, determine: (g=10m/s²)

a) deformação de cada mola.

b) o comprimento de cada mola

c) a deformação total do conjunto

Resolução comentada dos exercícios de vestibulares sobre

Associação de molas

1- Período T da mola da figura 1  ---  T = 2π√m/k

Como as molas estão associadas em paralelo, a constante elástica da mola equivalente, que, substituindo as duas produz o mesmo efeito será k_e = k + k  ---  k_e =2k e seu período será T’ = 2π√m/2k  ---  T’ = 2π√m/k.1/√2.

T/T’ = √2  ---  T’ = T/√2  --- racionalizando  ---  T’= T√2/2  Resposta C

2-

a) Como as duas molas de constantes k₂ estão em para, a mola equivalente terá constante k_e1 =30 + 30 = 60N/m. Então teremos:

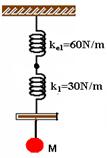
As duas molas acima estão em série, então a mola equivalente terá constante k_e, dada por: 1/k_e = 1/60 + 1/30  ---  k_e = 20N/m,

que é a constante elástica total  equivalente do conjunto.

b) T = 2p√m/k  ---  T = 2p√20/9 /20  ---  T = 2.3.1/3  ---  T=2s  ---  f=1/T  ---  f=0,5Hz

3-

As 3 molas de constantes k₂ estão em paralelo e serão substituídas por uma única mola de constante k_e1=3k₂.

As duas molas de constantes k₁ também estão em paralelo e serão substituídas por um única mola de constante k_e2=2k₁

Então, teremos:

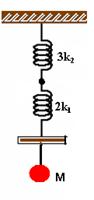
A mola resultante das duas acima, que estão em série, terá k_e, tal que: 1/k_e = 1/3k₂ + 1/2k₁  ---  1/k_e = 2k₁ + 3k₂ / 6k₁.

K_e = 6k₁.k₂ / 2k₁ + 3k₂

O período desse sistema vale  ---  T = 2pÖm/6k₁.k₂ / 2k₁ + 3k₂  ---  T = 2pÖm(2k₁ + 3k₂)/6k₁.k₂

F = 1/T = 1/2p√6k₁.k₂ / m(2k₁ + 3k₂)

4-

a) A mola inteira (mola equivalente) tem constante elástica k’=10N/m sendo que 1/k’= 1/k + 1/k +1/k, onde k é a constante elástica de cada parte.

1/k’=3/k  ---  1/12 = 3/k  ---  k =36N/m

b) Paralelo  ---  k­e=36 + 36 +36  ---  k_e=108N/m  ---  T=2π√m/k_e  ---  T=2π√0,1/108  --- T = 6.10^-2.π s

c) Série  ---  k_e=12N/m  ---  T=2π√m/k_e  ---  T=2π√0,1/12  ---  T= 18.10^-2.π s

5-

a) Peso de cada massa  ---  P=mg  ---  P=0,01.10  ---  P=0,1N. Como as molas são ideais, suas massas são desprezíveis.

Observe que a mola 1 está sujeita à força F=0,3N (são as 3 massas que estão deformando-a)

F₁=k₁.x₁  ---  0,3=0,1.x₁  ---  x₁ = 3cm

A mola 2 está sujeita à F=0,2N (apenas duas massas estão deformando-a)

F₂=k₂.x₂  ---  0,2=0,1.x₂  ---  x₂= 2cm

Mola 3  ---  F₃=k₃.x₃  ---  0,1=0,1.x₃  ---  x₃= 1cm

b) mola 1 – L₁= 23cm

    mola 2 – L₂= 22cm

    mola 3 – L₃= 21cm

c) 6 cm