Segunda lei de Newton ou Princípio Fundamental da Dinâmica

Ao contrário da primeira lei de Newton que justifica o que ocorre com um corpo quando a força resultante que age sobre ele for nula, esta segunda lei de Newton explica o que acontece com esse corpo quando a resultante das forças que agem sobre ele não for nula.

Podemos definir o Princípio Fundamental da Dinâmica ou segunda lei de Newton do seguinte

modo:

Assim, se essa força resultante for constante, a aceleração (variação de velocidade), por ela produzida também será constante e a força e a aceleração são grandezas diretamente proporcionais, ou seja:

Como F = m.a é uma função do 1^O grau, o gráfico da intensidade (F) da força aplicada a um corpo, em função de sua aceleração (a) é uma reta inclinada cuja inclinação ou coeficiente angular representa a massa do corpo, que é uma constante de proporcionalidade.

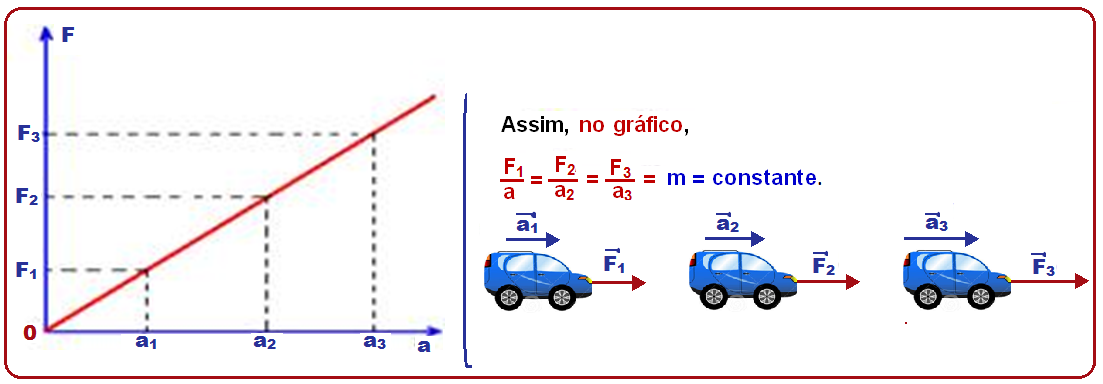
Essa constante de proporcionalidade (m), que é característica de cada corpo recebe o nome de massa inercial ou simplesmente massa e corresponde à medida da inércia do corpo, ou seja, da resistência que o corpo oferece à variação do vetor velocidade.

Observe na lei fundamental da Dinâmica (F = m.a) que, quanto maior a massa do corpo, maior será sua inércia, ou seja, devemos aplicar uma força resultante maior para acelerar ou retardar um caminhão

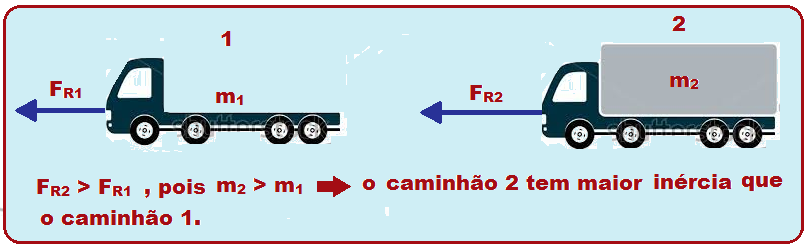
carregado (maior massa) do que o mesmo caminhão descarregado (menor massa).

Unidades e significado de força no sistema internacional de unidades (SI):

F intensidade da força resultante newton (N)

M massa do corpo quilograma (kg)

a aceleração do corpo (m/s²)

Considerando, m = 1 kg, a = 1m/s² e F = 1N, podemos definir 1N como sendo a intensidade da força resultante que, aplicada sobre um corpo de massa 1 kg, produz no mesmo uma aceleração de 1m/s².

Peso (P) de um corpo

Podemos determinar o peso P de um corpo (força vertical para baixo, com que a Terra atrai o corpo) pela expressão P = m.g, onde m é a massa do corpo e g a aceleração da gravidade.

Assim, pela segunda lei de Newton se a força peso for a resultante sobre o corpo, temos, em intensidade:

O que você deve saber, informações e dicas

A massa é sempre uma grandeza escalar positiva.

A força da expressão é a força resultante, que é a soma vetorial de todas as forças que

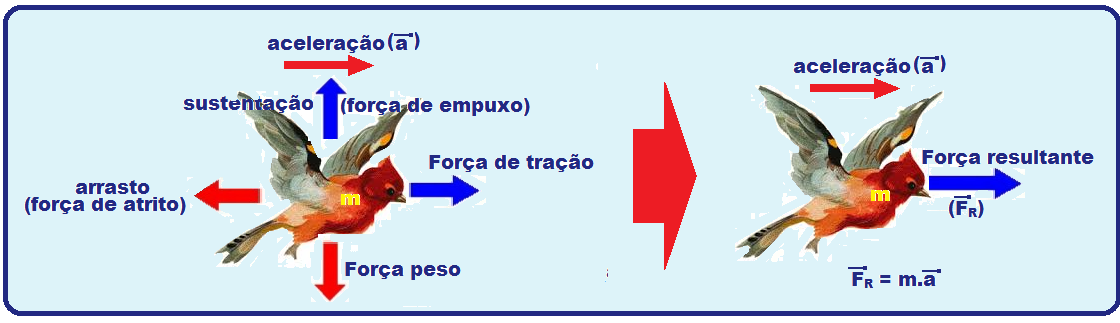
agem sobre o corpo.

Um dinamômetro ideal inserido numa corda ideal (inextensível e de massa desprezível), indica a

intensidade da força de tração numa das extremidades da mesma (figura acima).

Se tivermos dois ou mais dinamômetros ideais ligados conforme a figura abaixo e na extremidade

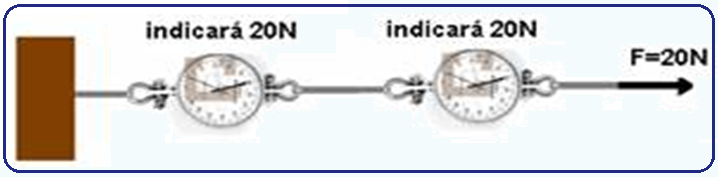
livre do dinamômetro da direita aplicarmos uma força, por exemplo de 20N, cada dinamômetro indicará 20N.

Exemplos:

Se a trajetória for retilínea a força resultante e a aceleração tem sempre a mesma direção que a velocidade, mas podem ter sentidos opostos (vide figuras abaixo)

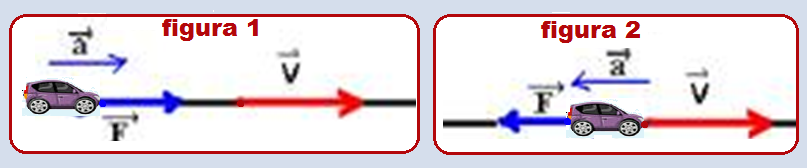
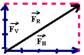
Na figura 1, o corpo se move em direção horizontal e sentido para a direita, obedecendo ao vetor velocidade. Observe também que estas são a direção e sentido da força resultante e da aceleração. Trata-se de um movimento retilíneo acelerado.

Na figura 2, o corpo se move em direção horizontal e sentido para a direita (veja a direção e o sentido do vetor velocidade), mas a força resultante e aceleração estão para a esquerda, freando-o.

Trata-se de um movimento retilíneo retardado.

Lembre-se de que o deslocamento do corpo e sua velocidade vetorial são sempre coincidentes.

Se o movimento do corpo for curvilíneo, a força resultante e consequentemente a aceleração tem sempre direção e sentido diferentes da velocidade.

Como exemplo, na figura abaixo temos uma bola lançada obliquamente, onde, desprezando-se a resistência do ar, a força resultante sobre a mesma que é seu peso e a aceleração que é a da gravidade g

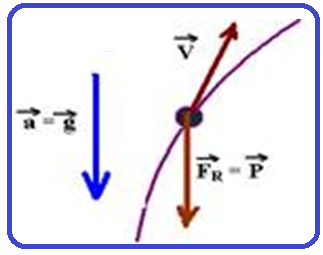
(ambas verticais e para baixo), têm direção e sentido diferentes da velocidade que é sempre tangente em cada ponto.

Se o movimento do corpo for circular e uniforme a força resultante e consequentemente a aceleração

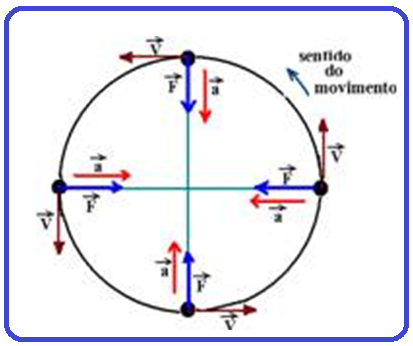
(centrípeta) são dirigidas sempre para o centro da circunferência não coincidindo com a velocidade que é sempre tangente à trajetória em cada ponto.

Pela segunda lei de Newton se a força peso for a resultante sobre o corpo, temos, em intensidade:

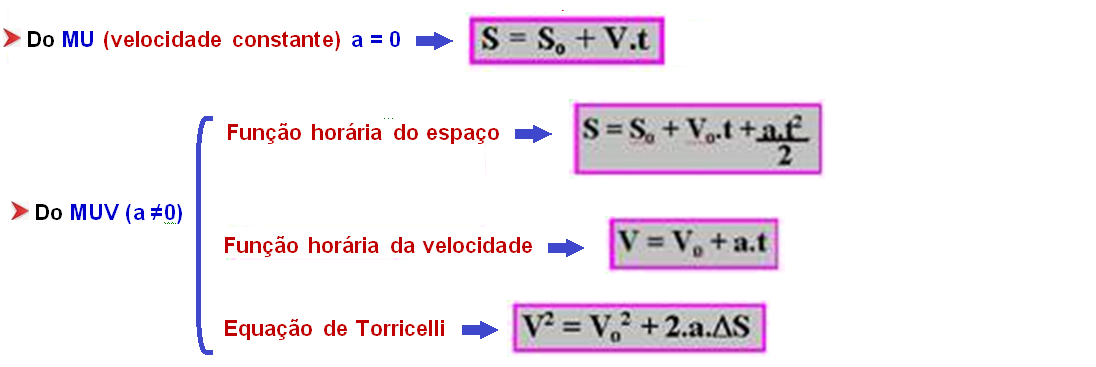
Equações da Cinemática

Exercícios de vestibulares sobre o princípio fundamental da Dinâmica ou segunda lei de Newton

01-(UFB) Determine a intensidade, direção e sentido do vetor aceleração de cada corpo a seguir, sendo fornecidas as massas e as forças aplicadas em cada um:

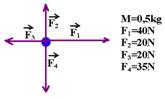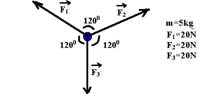a) b) c)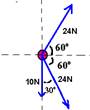

02-(UEL-PR) Considere a figura a seguir

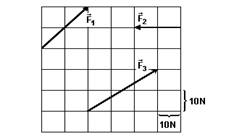
O módulo de sua resultante das três forças, em N, é

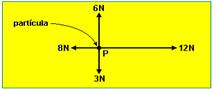
03-(PUC-MG) Sobre uma partícula P agem quatro forças, representadas na figura abaixo. O módulo da força resultante sobre a partícula é de:,

04-(ITA-SP) Dois dinamômetros A e B, estão ligados como mostra a figura. Sejam F₁ e F₂as leituras dos dinamômetros A e B, respectivamente, quando se aplica uma força F na extremidade livre do dinamômetro B. Nestas condições, podemos afirmar que:

a) F=F₁ + F₂=2F₁

b) F=F₁ + F₂=3F₂

c) F=F₂=2F₁

d) F=F₁=F₂

e) F=F₁=2F₂

05-(PUC-BA) A figura abaixo representa um gráfico do módulo (F) da força aplicada a um corpo, em função de sua aceleração (a).

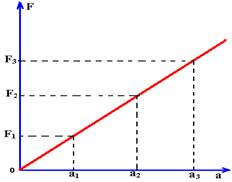
O que representa o coeficiente angular, ou inclinação da reta do gráfico?

a) a massa do corpo
b) a velocidade do corpo
c) o espaço percorrido pelo corpo
d) a quantidade de movimento do corpo
e) a energia cinética do corpo.

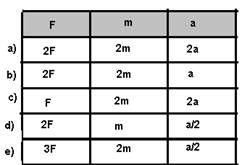
06-(UNESP-SP) Submetendo-se a partícula de massa m a uma resultante , a aceleração impressa é . Aplica-se a lei fundamental da dinâmica =m. . Esses dados estão inscritos na primeira linha do quadro a seguir. Assinalar outro conjunto de elementos coerentes com os dados.

07-(UFMG-MG) O gráfico abaixo representa a velocidade em função do tempo, de uma partícula de massa m=2kg, que se desloca em linha reta.

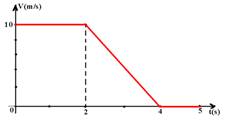
Qual dos gráficos representa melhor o módulo da força resultante que atuou na partícula durante os 5s de seu movimento?

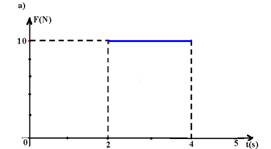
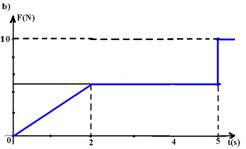
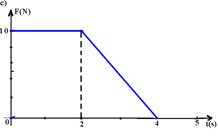
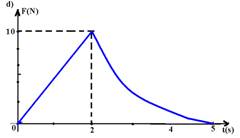
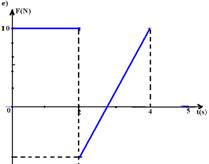
08-(FUVEST-SP) Um corpo de 5 kg descreve uma trajetória retilínea que obedece à seguinte equação horária S=3t² + 2t + 1, onde S é medido em metros e t em segundos.Determine o módulo da força resultante sobre o corpo.

09-(FUVEST-SP) Numa cobrança de pênalti, o goleiro segurou a bola no peito. A bola tinha uma massa de 0,40kg e alcançou o goleiro com uma velocidade de módulo 20m/s.

O choque durou um intervalo de 0,10s.

Qual a intensidade da força média que o goleiro aplicou na bola?

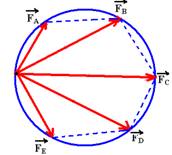
10-(MACKENZIE-SP) A figura mostra 5 forças representadas por vetores de origem comum, dirigidas aos vértices de um hexágono regular. Sendo 10N o módulo da força , a intensidade da resultante dessas 5 forças é:

11-(CEFET-PR) Aplicadas a um corpo são mostradas três forças coplanares. O sistema de eixos está graduado em newtons para avaliar a intensidade de cada uma delas.

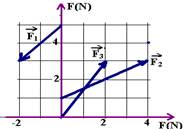
È possível afirmar que a força resultante no corpo tem um módulo, em newtons, igual a:

12-(UFRS) Para um observador inercial, um corpo que parte do repouso, sob ação exclusiva de uma força F constante, adquire a velocidade v de módulo 5 m/s após certo intervalo de tempo. Qual seria, para o mesmo observador, o módulo da velocidade adquirida pelo corpo, após o mesmo intervalo de tempo, supondo que ele já tivesse inicialmente a velocidade v e que a força exercida sobre ele fosse 4F?

13-(PUC-PR) A aceleração adquirida por um automóvel é de 1,5 m/s² e a força resultante que age sobre ele é 3000 N.

Com base nessas informações, analise as proposições:

I. A massa do automóvel é igual a 2000 kg.

II. A massa do automóvel é igual a 4500 N.

III. Se o automóvel partir do repouso, após 4 segundos sua velocidade será igual a 6 m/s.

IV. Se o automóvel partir do repouso, após 2 segundos terá percorrido um espaço igual a 1,5 metros.

V. Se quisermos reduzir a aceleração à metade, basta dividirmos por dois a intensidade da força aplicada.

Estão corretas:

14-(PUC-RJ) Existem bolas de boliche de diversas massas. Suponha que você jogue, com forças iguais, três bolas, uma de cada vez. A primeira tem massa m₁=m, a segunda m₂=m/2 e a terceira m₃=2m. Suas respectivas acelerações são:

a) a₂=2.a₁, a₃=a₁/2

b) a₂=a₁/2, a₃=2.a₁

c) a₁=a₂=a₃

d) a₂=a₁/3, a₃=2.a₁/3

e) a₂=3.a₁, a₃=3.a₁/2

15-(UFF-RJ) Uma pessoa mediu, sucessivamente, as acelerações produzidas em dois blocos, 1 e 2, pelas correspondentes forças resultantes que sobre ele atuaram. O gráfico abaixo expressa a relação entre as intensidades dessas forças e de suas respectivas acelerações.

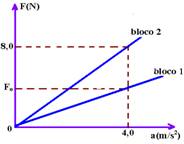
Se o valor da massa do bloco 1 é igual a três quartos do valor da massa do bloco 2, podemos afirmar que o valor de F_o indicado no gráfico é:

16-(PUC-MG) No livro de Jonathan Swift "As viagens de Gulliver", o viajante imaginário Lemuel Gulliver passou um tempo de sua vida no reino de Lilliput, onde todas as coisas vivas - homens, árvores, grama - eram semelhantes às de nosso mundo, exceto pelo fato de serem formadas em uma escala muito pequena.

Os lilliputianos, por exemplo, não tinham mais do que 15 cm de altura e eram construídos proporcionalmente como nós.

Gulliver visitou também Brobdgnag, um país de coisas gigantes, cujos habitantes eram exatamente como nós, porém, 12 vezes maiores. Na realidade, Lilliput e Brobdgnag não existem.

Galileu (1564-1642), no seu trabalho "Duas Novas Ciências", mostra, através de diálogos entre uma pessoa de senso comum e um cientista, que modelos muito pequenos ou muito grandes de homens não poderiam ser como nós. Baseados no texto de "Duas Novas Ciências", pode-se concluir que o peso de um habitante de Brobdgnag seria aproximadamente 1728 vezes o nosso, e seus ossos seriam 144 vezes mais resistentes.

Considere, por exemplo, um cubo de lado L apoiado sobre uma superfície horizontal, sem atrito sobre o qual atua uma força F.

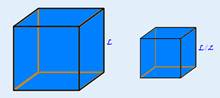
Observa-se que, quando a força F é aplicada a este corpo, ele percorre ao final de 10 s uma distância de 80m. Se um cubo idêntico a este, mas de lado L/2, for submetido à mesma força F, ao final dos mesmos 10s ele percorrerá uma distância de:

17-(UESPI-PI) Segundo a primeira lei de Newton, é correto afirmar que:

a) uma partícula com o módulo, a direção e o sentido de sua velocidade constantes tem a força resultante, agindo sobre ela, nula.

b) uma partícula com o módulo de sua velocidade constante tem a força resultante, agindo sobre ela, nula.

c) uma partícula com o módulo e o sentido de sua velocidade constantes tem a força resultante, agindo sobre ela, nula.

d) uma partícula com a direção e o sentido de sua velocidade constantes tem a força resultante, agindo sobre ela, nula.

e) uma partícula com o módulo, a direção e o sentido de sua aceleração constantes tem a força resultante, agindo sobre ela, nula.

18-(UNCISAL-AL) Sobre as forças que ocorrem em aviões a jato, são feitas as afirmações a seguir:

I. a força resultante sobre um avião a jato, lotado de passageiros, bagagens e tripulação, voando em velocidade de cruzeiro, constante, em trajetória horizontal e retilínea, é nula;

II. imediatamente após a decolagem, enquanto sobe, a força resultante sobre o avião é sempre vertical e dirigida para cima;

III. após pousar na pista, para garantir eficiência durante a frenagem, a força resultante sobre o avião é, necessariamente, mais intensa que seu peso.

Está correto o contido em

a) I, apenas.

b) II, apenas.

c) I e II, apenas.

d) II e III, apenas.

e) I, II e III.

19-(UFT-TO) Assinale a afirmativa abaixo que NÃO é sempre verdadeira:

a) No movimento circular uniforme de um determinado objeto existe força atuando no objeto.

b) Se um objeto está acelerado é porque existem forças atuando sobre ele e sua velocidade muda com o passar do tempo.

c) Se existem forças atuando sobre um objeto, ele está acelerado e sua velocidade muda com o passar do tempo.

d) No movimento circular uniforme de um objeto existe aceleração do objeto e, portanto, a velocidade do mesmo muda com o passar do tempo.

e) No movimento circular uniforme de um determinado objeto não existe aceleração angular.

20-(FUVEST-SP) Uma pessoa pendurou um fio de prumo no interior de um vagão de trem e percebeu, quando o trem partiu do repouso, que o fio se inclinou em relação à vertical. Com auxílio de um transferidor, a pessoa determinou que o ângulo máximo de inclinação, na partida do trem, foi 14°.

inclinação, na partida do trem, foi 14°. Nessas condições,

a) represente, na figura da página de resposta, as forças que agem na massa presa ao fio.

b) indique, na figura da página de resposta, o sentido de movimento do trem.

c) determine a aceleração máxima do trem.

NOTE E ADOTE:

tg 14° = 0,25.

aceleração da gravidade na Terra, g = 10 m/s².

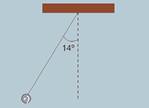
Dados: g = 10 m/s²; tg 14° = 0,25.

21-(UDESC-SC) Um trailer é rebocado, a partir do repouso, por um carro em uma rodovia plana e retilínea, conforme ilustra a figura. A força resultante sobre o trailer mantém constantes a direção e o sentido. O módulo da força varia com o tempo, de acordo com o gráfico apresentado:

Em relação a esta situação, analise:

I – O trailer é uniformemente acelerado nos seguintes intervalos de tempo: 0 a t₁ e t₄ a t₅.

II – A velocidade do trailer atinge seu valor máximo no instante t₄.

III – No intervalo t₄ a t₅ a velocidade do trailer é constante, pois a força resultante sobre ele é zero.

Assinale a alternativa correta.

a) Somente a afirmativa I é verdadeira.

b) Somente as afirmativas I e III são verdadeiras.

c) Somente as afirmativas II e III são verdadeiras.

d) Somente a afirmativa III é verdadeira.

e) Todas as afirmativas são verdadeiras.

22-(CPS-SP) Na figura que se segue estão representadas as únicas forças que agem no bloco homogêneo de massa igual a 2 kg.

Considere:

de intensidade igual a 2N

de intensidade igual a 3N.

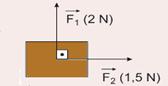
O valor do módulo da aceleração que o bloco adquire, em m/s², vale

23-(UECE-CE) Uma única força agindo sobre uma massa de 2,0 kg fornece a esta uma aceleração de 3,0

m/s². A aceleração,em m/s², produzida pela mesma força agindo sobre uma massa de 1 kg é

a) Zero.

b) 1,5.

c) 3,0.

d) 6,0.

(PUC-MG) TEXTO PARA AS PRÓXIMAS 2 QUESTÕES:

Estudando-se o movimento de um objeto de massa 2kg, obteve-se o gráfico velocidade x tempo a seguir. A velocidade está em m/s e o tempo, em segundo.

24-(PUC-MG)

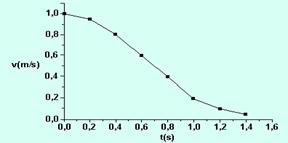
É CORRETO afirmar que a distância percorrida pelo objeto entre t = 0 e t = 1,4s foi aproximadamente de:

25-(PUC-MG)

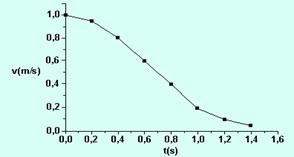
Entre os instantes t = 0,4s e t = 0,8s o módulo da força resultante sobre o objeto foi aproximadamente de:

26-(UFU-MG) Um objeto é lançado verticalmente na atmosfera terrestre. A velocidade do objeto, a aceleração gravitacional e a

resistência do ar estão representadas pelos vetores , e , e , respectivamente.

Considerando apenas estas três grandezas físicas no movimento vertical do objeto, assinale a alternativa correta.

27-(PASES) Um elevador ora se encontra em repouso, ora sobe com velocidade de módulo constante V,

ora desce com velocidade de módulo constante 2V. Indicando-se por T_o , T₁ e T₂, respectivamente, as trações no cabo desse elevador quando ele está parado, ou subindo ou descendo nessas condições, é CORRETO afirmar que a relação entre essas tensões é:

a) T₂ < T₁ < T_o

b) T₂ > T₁ > T_o

c) T₂ > T0 > T₁

d) T₂ = T₁ = T_o

28-(UNESP-SP) Num jato que se desloca sobre uma pista horizontal, em movimento retilíneo uniformemente acelerado, um

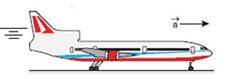
passageiro decide estimar a aceleração do avião. Para isto, improvisa um pêndulo que, quando suspenso, seu fio fica aproximadamente estável, formando um ângulo θ= 25^o com a vertical e em repouso em relação ao avião. Considere que o valor da aceleração da gravidade no local vale 10 m/s², e que sen 25^o = 0,42; cos 25^o = 0,90; tan 25^o = 0,47. Das alternativas, qual fornece o módulo aproximado da aceleração do avião e melhor representa a inclinação do pêndulo?

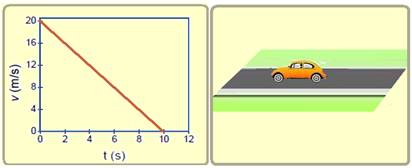
29-(FGV-RJ)

A figura abaixo apresenta o gráfico do módulo da velocidade v em função do tempo t de um carro com 1000 kg de massa. O módulo da força resultante que atua no carro e a distância por ele percorrida entre t = 0 s e t = 5 s são, respectivamente, iguais a

A. 2000 N e 125 m

B. 2000 N e 50 m

C. 2000 N e 75 m

D. 10000 N e 125 m

E. 10000 N e 75 m

Instrução: As questões 30 e 31 devem ser respondidas com base na situação física descrita a seguir.

No esquema apresentado na figura abaixo, uma partícula de poeira cósmica, cuja massa é igual a 2,0 g, move-se livremente de norte para o sul, com velocidade de módulo igual a 1,2 km/s. No instante visualizado nesse esquema (t = 0), passam a atuar sobre essa partícula as forças A, B e C nele representadas, sendo todas elas constantes.

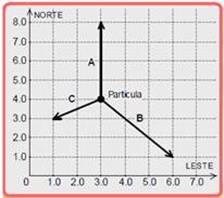
Considere também que os valores numéricos associados aos eixos “norte” e “leste” referem-se à unidade de força do Sistema Internacional: newton (N).

30-(IFNMG-MG)

O módulo da velocidade da partícula no instante t = 1,0 s, expresso em km/s, está corretamente apresentado na alternativa:

31-(IFNMG-MG)

No instante t = 1,0 s, as forças A, B e C deixam de atuar na partícula. Nessas condições, a forma da trajetória da partícula, desde t = 0, está corretamente descrita na alternativa:

A) Retilínea, desde t = 0, e ainda retilínea, após t = 1,0 s.

B) Inicialmente circular e, após 1,0 s, retilínea.

C) Inicialmente circular e, após 1,0 s, parabólica.

D) Inicialmente parabólica e, após t = 1,0 s, retilínea.

Considere as leis de Newton e as informações a seguir para responder às questões de números 32 e 33

Uma pessoa empurra uma caixa sobre o piso de uma sala. As forças aplicadas sobre a caixa na direção do movimento são:

F_p: força paralela ao solo exercida pela pessoa;

F_a: força de atrito exercida pelo piso;

A caixa se desloca na mesma direção e sentido de F_p.

A força que a caixa exerce sobre a pessoa é F_c.

32-(UERJ-RJ)

Se o deslocamento da caixa ocorre com velocidade constante, as magnitudes das forças citadas apresentam a seguinte relação:

(A). F_p = F_c = F_a

(B). F_p > F_c = F_a

(C). F_p = F_c> F_a

(D). F_p = F_c < F_a

33-(UERJ-RJ)

Se o deslocamento da caixa ocorresse com aceleração constante, na mesma direção e sentido de F_p, as magnitudes das forças citadas apresentam a seguinte relação:

(A). F_p = F_c = F_a

(B). F_p > F_c = F_a

(C). F_p = F_c> F_a

(D). F_p = F_c < F_a

Resolução comentada dos exercícios de vestibulares sobre o Princípio Fundamental da Dinâmica ou Segunda lei de Newton

01-

a) Na vertical --- 35N-20N=15N (para baixo) Na horizontal --- 40N-20N=20N (para a direita)

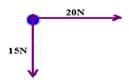
Efetuando a adição vetorial

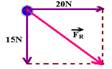
Aplicando Pitágoras --- F_R² = (15)² + (20)² --- F_R = 25N

F_R = m.a --- 25=0,5.a --- a=50m/s² --- a direção e sentido de a é sempre a mesma que de F_R

b) Quando as três forças tiverem a mesma intensidade e o ângulo entre elas for de 120^o a força resultante é nula e consequentemente a aceleração também será, ou seja, .

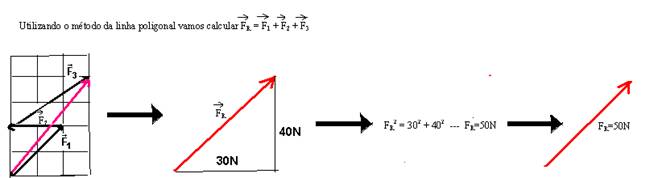
c) Somando vetorialmente as duas forças de 24N e aplicando a lei dos cossenos:

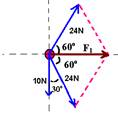
F₁² = (24)² + (24)² + 2.24.24.cos120^o --- F₁² = (24)² + (24)² + 2.(24)².(-1/2) --- F₁=24N

Então teremos:

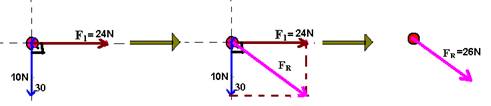
Aplicando Pitágoras --- F_R² = (24)² +(10)² --- F_R=26N

02-

03- Na vertical --- 3N para cima. --- Na horizontal --- 4N para a direita --- Aplicando Pitágoras --- 5N --- R- A

04- D

05- A

06- A alternativa a é falsa, pois 2F=2m.2a --- 2F=4ma --- F=2ma

A alternativa b é correta, pois 2F=2m.a --- F=ma

A alternativa c é falsa, pois F=2m.2a --- F=4ma

A alternativa d é falsa, pois 2F=m.a/2 --- F=(ma)/4

A alternativa e é falsa, pois 3F=2m.a/2 --- F=(ma)/6

07- Entre 0 e 2s, a velocidade é constante e a trajetória reta, portanto trata-se de um MRU (equilíbrio dinâmico) e a força resultante é nula. Entre 2s e 4s, o movimento é desacelerado e a aceleração vale --- a=(V - V_o)/t – t_o --- a=(0-10)/(4-2)

--- a= - 5m/s² --- a força resultante é constante e vale F=m.a --- F=2.(-5) --- F= -10N --- como o exercício pede o módulo --- F=10N. R- A

08- Da equação fornecida --- a=6m/s². --- F=m.a --- F=5.6 --- F=30N

09- V=V_o + a.t --- 0=20 + a.0,10 --- a= -20/0,10 --- a= - 200m/s² --- F=m.a --- F= -0,40.200 --- F= -80N --- módulo --- F=80N

10- Observando a figura abaixo, concluímos que e que, .

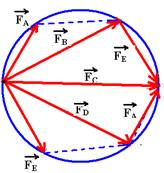
Como a força resultante é a soma vetorial de todas as forças temos ---

--- --- F=3.10 --- F=30N

11- Decompondo cada força na horizontal --- --- ---

Resultante na horizontal --- --- F_H=4N

Decompondo cada força na vertical

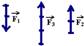
Resultante na vertical:

Então teremos:

Aplicando Pitágoras --- F_R=5N

12-1^o movimento --- F=ma --- m=F/a 2^o movimento --- 4F=ma₁ --- m=4F/a₁ --- F/a=4F/a₁ --- a₁=4a

1^o movimento --- V=V_o + a.t --- 5=0 + a.t --- a.t=5

2^o movimento --- V₁=V_o + a₁.t --- V₁=5 + 4.a.t --- V₁=5 + 4.5 --- V₁=25m/s R- C

13- F=ma --- 3.000=m.1,5 --- m=2.000kg --- I – correta --- II - falsa

V=V_o+a.t --- V=0+1,5.4 --- V=6m/s --- III - correta

DS=V_o.t + a.t²/2 --- DS=0.2 + 1,5.4/2 --- DS=3m --- IV - falsa

V – correta --- m=F/a=constante --- F e a são diretamente proporcionais

R – C

14- Observe na segunda lei de Newton que: F=m.a --- a=F/m --- a e m são inversamente proporcionais --- R- A

15- m₁=3m₂/4 --- a₂=a₁=4m/s² --- F₂=m₂.a₂ --- m₂=8/4 --- m₂=2kg --- m₁=(3.2)/4 --- m₁=1,5kg --- F_o=m_1.a₁ --- F_o=1,5.4 --- F_o=6N.

16- Cálculo da aceleração do cubo de lado L --- ΔS=V_ot + at²/2 --- 80=0 + a.10²/2 --- a=1,6m/s² --- como o novo cubo é idêntico ao anterior, eles possuem a mesma densidade --- d=m/v --- d=m/(L/2)³ --- observe na expressão anterior que, se o volume fica 8 vezes menor, a massa também ficará 8 vezes menor, pois a densidade é constante --- F=ma ---

Sendo a força F a mesma, se a massa fica 8 vezes menor a aceleração deverá ficar 8 vezes maior --- nova aceleração --- a=8x1,6 --- a=12,8m/s² --- ΔS’=V_ot + at²/2=0 + 12,8.10²/2 --- ΔS’=640m --- R- C

17- R- A --- Princípio da inércia

18- I. Correta --- Princípio da Inércia

II. Correta --- se ele sobe a força resultante sobre ele tem que ser para cima.

III. Correta --- Correta --- quanto maior a força de compressão com o solo, maior será a força de atrito

R- E

19- Se existem forças agindo sobre um objeto ele não está necessariamente acelerado o que ocorre somente se a intensidade da força resultante for diferente de zero --- mas, se essas forças se anularem ele estará em repouso ou em MRU --- R- C

20- a) As forças que agem na massa pendular são o peso e a tração.

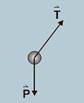
b) Como o movimento é retilíneo, a componente vertical da resultante é nula --- T_y=P --- A resultante é então na direção

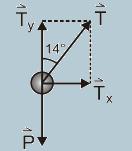
horizontal --- F_R= T_X --- como o vagão parte do repouso, ele acelera no sentido da resultante, ou seja, para a direita ---

c) Do princípio fundamental da dinâmica --- F_R = m a --- T_X = m a_max --- como, na vertical, a componente da resultante é nula --- T_y = P = m g --- tg14^o=T_X/T_y=m.a_Max/m.g --- 0,25=a_max/10 --- a_max=10.0,25 --- a_max=2,5m/s²

21- (I) Incorreta --- o trailer é uniformemente acelerado apenas no intervalo 0 a t₁, onde a resultante tem intensidade constante.

(II) Correta --- até o instante t₄ há uma força resultante acelerando o trailer, fazendo sua velocidade aumentar.

(III) Correta --- se a resultante é nula, o movimento retilíneo e uniforme.

R- C

22- Intensidade da resultante dessas forças --- F_R²=F₁² + F₂² --- F_R=√(2² + 1,5² --- F_R=2,5N --- pelo princípio fundamental da dinâmica --- F_R=ma --- 2,5=2.a --- a=1,25m/s² --- R- A

23- F₁=m₁.a₁ --- F₁ = 2 (3) --- F₁ = 6 N --- F₁=F₂=F = m₂ a₂ --- 6 = 1 a₂ --- a₂ = 6 m/s² --- R- D

R- D

24- A distância percorrida em um diagrama de velocidade versus tempo é dada pela área sob a linha de gráfico --- aproximando esta figura para um triângulo retângulo --- d=base.altura/2=1,4.1/2 --- d=0,7m --- R- A

25- a=(V – V_o)/(t – t_o)=(0,4 – 0,8)/0,8 – 0,4 --- a=-1m/s² --- pela segunda lei de Newton --- F=ma=2.(-1) --- F=-2N --- R- A

26- O vetor velocidade é tangente à trajetória e é vertical e para cima na subida e vertical e para baixo na descida --- a aceleração da gravidade tem sempre direção vertical e sentido para baixo --- a força de atrito tem direção do movimento e sentido contrário a ele, ou seja, ao vetor velocidade --- R- A

27- A força resultante sobre o elevador é nula (P=T) se ele estiver subindo ou descendo em movimento retilíneo e uniforme ou em repouso --- R- D

28- Se o avião acelera para frente, por inércia, o corpo pendurado no fio tende a ficar parado em relação à pista e, portanto, vai para trás em relação ao avião --- o fio inclina-se para a esquerda --- a aceleração do avião será dada por --- a = g.tan 25^o = 10.0,47 ---

a = 4,7 m/s² --- R- A

29-

Em todo gráfico V x t a distância percorrida é numericamente igual à área hachurada, entre 0 e 5s, da figura abaixo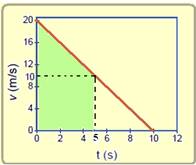

--- ∆S=área --- ∆S=(B + b).h/2=(20 + 10).5/2 --- ∆S=75m --- cálculo da aceleração do carro pelo gráfico --- a=(V – V_o)/(t – t_o)=(0 – 20)/(10 – 0) --- a=- 2m/s² --- força resultante --- F_R=m.a=1000.(-2) --- F_R=- 2000N em módulo F_R=2000N --- R- C.

30- Para calcular a intensidade da força resultante que age sobre a partícula cósmica você pode decompor as forças nas direções norte e leste --- observe na sequência abaixo que a intensidade da força resultante é de 1N no sentido leste ---

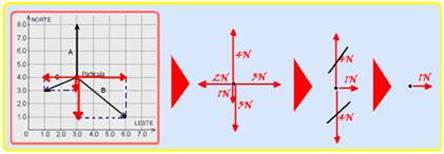
Como a velocidade inicial da partícula tem intensidade V_o=1200m/s do norte para o sul e a força resultante sobre ela tem intensidade 1N do oeste para leste, o movimento da partícula tem as características de composição de dois movimentos, um no sentido leste e outro no sentido sul (veja figura) --- no sentido leste, a projeção da velocidade inicial é nula V_oL=0 e ela se desloca sob ação de uma força resultante de valor F_R=1N e com aceleração --- F_R=m.a --- 1=2.10^-3.a --- a= 500m/s² --- sua velocidade nessa direção após t=1s terá intensidade --- V_L=V_oL + a_L.t=0 + 500.1 --- V_L=500m/s --- no sentido sul ela será lançada para baixo com V_oS=1200m/s, acelerando com aceleração da gravidade g=10m/s² --- após t=1s, sua velocidade nessa direção será --- V_S=V_oS + g.t=1200 + 10.1=1210m/s ---

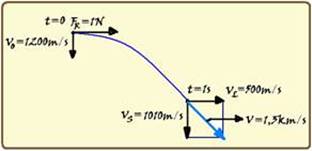
observe na figura que essas duas velocidades são perpendiculares e, aplicando Pitágoras você obterá V² = V_L² + V_S²=(500)² + (1210)² --- V=√(1714100) --- V=1309m/s=1,3km/s --- R- A.

31-

Pelo princípio da inércia, se as forças deixarem de atura, a força resultante sobre ela será nula e, após esse innstante, por inércia, ela seguirá em MRU com velocidade constante de 1,3km/s --- observe na resolução do exercício anterior (08) que, antes de 1s a trajetória era parabólica --- R- D.

32-

Se o deslocamento ocorresse com velocidade constante a força resultante sobre a caixa seria nula --- nesse caso, a

força que a pessoa exerce sobre a caixa tem que ter a mesma intensidade que a força de atrito --- note que a força que a pessoa exerce sobre a caixa tem a mesma intensidade que a força que a caixa exerce sobre a pessoa (princípio da ação e reação) --- R- A

33-

Nesse caso, como existe aceleração a resultante das forças sobre a caixa é diferente de zero --- F_R=m.a --- como a

caixa se desloca na mesma direção e sentido que F_p --- F_p – F_a=m.a --- F_p >F_a --- note que a força que a pessoa exerce sobre a caixa tem a mesma intensidade que a força que a caixa exerce sobre a pessoa (princípio da ação e reação) --- R- C