Resolução comentada dos exercícios de vestibulares sobre MHS Sistema massa-mola
Resolução comentada dos exercícios de vestibulares sobre
MHS Sistema massa-mola
01.a) F(t) = ma — F(t) = mw2Acos(wt + j)
b) mw2Acos(wt = j) = mw2x — x(t) = A cos(wt + j)
c) Usando as equações para a energia cinética e potencial, juntamente com as equações horárias da posição e velocidade, temos que k
Ec(t) = 1/2mv2(t) = 1/2 m(wAsen(wt + j))2 = 1/2mw2A2sen2(wt +j) — Ec = 1/2 kA2 sen2(wt + j) Ep(t) = 1/2kx2(t) = 1/2 k(Acos(wt + j) )2 — Ep(t)=1/2kA2cos2(wt + j)
A energia mecânica é a soma da energia cinética com a energia potencial. Logo,
Emec = 1/2 kA2 sen2(wt + j) + 1/2kA2cos2(wt + j) — Em=1/2kA2(sen2(wt + j) + cos2(wt + j)) — Em=1/2kA2(1)
Em=1/2kA2, que é uma constante
02- E
03-
Em-1J A=0,5m Vmáxima=2m/s
Em=1/2.kA2 — 1=1/2.k.(0,5)2 — k=8N/m Em=1/2.mV2máxima — 1=1/2.m.(2)2 — m=0,5kg
T=2pÖm/k — T=2pÖ0,5/8 — T=2p.1/4 — T=p/2 s — f=1/T — f=1/p/2 — f=2/pHz
04-
01- Verdadera – a força elástica iguala a força peso no ponto médio onde a velocidade é máxima e a aceleração nula
02- Falsa – a velocidade da pessoa aumenta até o ponto médio e a partir daí começa a diminuir.
04- Falsa – pois, T=2pÖm/k
08- Verdadeira—veja equação acima
16- Falsa- a aceleração é nula no ponto médio, a partir do qual ela inverte seu sentido, retardando a pessoa.
05-
Em=kA2/2 (constante) e Em=m.v2máxima/2 —k.A2/2 = m.V2máxima/2 — k.A2 = m.V2máxima = constante, ou seja, k é inversamente proporcional a A, e Em é sempre constante — alternativa a
06-
a) Como ela está sujeita a apenas uma força, o movimento é horizontal e essa força é a força elástica.Quando x=1m — Ep=1J — Ep=k.x2/2 — 1=k.12/2 — k=2N/m. A amplitude A vale 2m, pois é aí que v=0.
Em=k.A2/2 — Em=2.22/2 — Em=4J
b) Quando x=0 — Ep=0 — Em=Ec + Ep — 4=mV2/2 + 0 — 4=0,5V2/2 — V=Ö16 — V=4m/s
c) Em=Ec + Ep — 4=Ec + k.x2/2 — 4=Ec + 2.12/2 — Ec=3J
07-
Vamos calcular o período T, que é o tempo que ele demora para efetuar um vai e vem completo.
T=2pÖm/k — T=2.3.Ö0,35/100 — T=6.5.10-2 — T@0,3s
0,3s —— 1 vai e vem completo
1,0s —— n
n@3,3 —– alternativa C
08-
a) Em=k.A2/2 — Ep=k.x2/2 — Ec=7/9.k.x2/2
Em= Ec + Eo — k.A2/2 = 7/9.k.x2/2 + k.x2/2 — k.A2/2 = (7.k.x2 + 9.k.x2)/18 — 9.k.A2 = 16.k.x2 — x = Ö9/16.A2
X = ± 3/4.A — Nas posições x = + 3/4.A e X = – 3/4.A
b) Sim. Por exemplo, no ponto O quando toda a energia mecânica estará na forma de energia cinética.
09-
(01) Falsa. A força elástica não é constante, pois varia de acordo com a deformação.
(02) Correta. Desprezando-se as forças externas dissipativas o sistema oscilará sempre.
(04) Correta — w =Ök/m — w = Ö200/2 — w = 10rad/s
(08) Falsa. A velocidade máxima do corpo vale — Vmáxima = w.A = 10.0,1 = 1,0m/s, mas não é no ponto de máximo deslocamento, mas sim na posição central 0.
(16) Correta. O período T é dado por T = 2pÖm/k — T = 2pÖ2/200 — T = 2p.1/10 — T = p/5 s.
Soma=(02 + 04 + 16) = 22
10-
Em X2 — Ep é máxima e Ec é nula. Em X1 — Ep = a — E = Ec + Ep — E = a + b — Ec + a = a + b — Ec = +b
R: C
11-
a) No equilíbrio — Fe = P — k.x = m.g — k = m.g/x — k = 0,4.10/0,05 — k=4/0,05 — k =80N/m
b) O movimento é um MHS e o seu período não depende da amplitude A e é fornecido pela expressão — T = 2.pÖm/k
T = 2pÖ0,4/80 — T = 2p.2,24 — T = 4,48p s
12-
a) Escolhendo qualquer ponto por exemplo, quando E — F = 0,75nN, x=-15nm. F =- k.x — 0,75.10-9 = -(-15).10-9.k —
k = 0,75/15— k = 0,05N/m.
b) T = 2pÖm/k — T = 2pÖ180.10-26/0,05 — T = 12p10-12 s — w =2p/T — w = 2p/12p10-12 — w = 1/6.1012rad/s
Vmáaima = w.A — Vmáxima = 1/6.1012.30.10-9 — Vmáxima = 5.103 m/s
13- Com o cubo em equilíbrio, a força resultante sobre ele é nula — empuxo = peso — ρ.g.v = m.g — 1.000v=81 —
V=0,081m3 — como a área da base é 1 m2, isto significa que o ponto de equilíbrio fica a 0,081 m ou 8,1 cm abaixo da linha da superfície, pois V=s.h — 0, 081=1.h — h=0,081m — o cubo é forçado para baixo, digamos uma profundidade x além de 0,081 m — a força resultante sobre o cubo funcionará como a força restauradora do MHS — Fresultante = Empuxo – Peso —
Fresultante = ρ.g.(0,081 + x) – m.g — Fresultante = ρ.g.0,081 + ρ.g.x – m.g = ρ.g.x — se esta força é a restauradora do MHS então ρ.g.x = k.x — k = ρ.g — frequência angular de um sistema oscilante — w=√(k/m)=√ (ρ.g/m)=√(1.000×10/81) — w=√(10.000/81) — w=100/9 rad/s — R- A
14- No MHS (movimento harmônico simples) o sistema apresenta energia potencial elástica máxima nas extremidades (A e –A) e energia cinética máxima no centro (0). Desta forma a velocidade da partícula no centro do sistema é dada por — mv2/2=kx2/2 —
0,05v2=20.(0,2)2 — v2=0,8/0,05 — v=√16 — v=4m/s — R- C
15- a) Expressão da frequência — f = (1/2π).√(k/m) — 30.103 = (1/2.3,14).√(k/5.10-3) — 30.6,28.103 = √(k/5.10-3) — (188,4.103)2 = k/5.10-3 — k=35.495.106.5.10-3 — k=1,77.108 N/m — energia potencial elástica — Ep=(1/2).k.∆x2 — Ep=0,5.1,77.108.(0,02.10-6)2 — Ep= 3.54.10-8 J
b) Expressão fornecida — (∆t/t)=(1/2).(∆L/L) — (∆t/1.800)=(1/2).(- 0,2)/90) — ∆t/1.800= – 1/900 — ∆t=-1.800/900 —
∆t= – 2s — novo intervalo de tempo — ∆t’= 1800 – 2 = 1798 s
16- Nas figuras abaixo — Ro: distância da extremidade fixa da mola até o centro de oscilação para o sistema não em rotação —
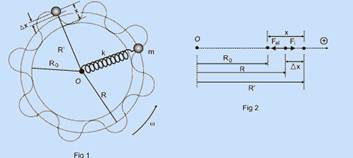
R: distância da extremidade fixa da mola até o centro de oscilação para o sistema em rotação — R’: distância da extremidade fixa da mola até um ponto qualquer da trajetória — x: deformação da mola — ∆x: variação da deformação entre o centro de oscilação em rotação e um ponto qualquer da trajetória — se o sistema apenas girasse sem oscilar, o movimento circular uniforme teria raio R — a força resultante sobre a partícula seria apenas a força elástica agindo como resultante centrípeta —
FR=Fc=Felétrica=mw2R=kx — mw2R=k(R – Ro) (I) — para o sistema girando e oscilando vamos considerar um referencial fixo ao oscilador (referencial não-inercial) — para esse referencial há um movimento oscilatório, com uma deformação aparente da mola igual a ∆x, quando a partícula está numa posição de raio R’
R — para esse referencial, temos que introduzir a “força de inércia” ou força centrífuga (Fi), dirigida para fora, oposta à força elástica, como mostrado na Fig 2 — nesse referencial, obedecendo ao sentido de orientação, a força resultante vale — FR= – Felétrica + Fi — m.a = -k.x + m∆2R’ (II) — figura 2 — x= (R’ – Ro) —
R’=∆x + R
— substituindo-os em (II) — ma = -k(∆x + R – Ro) + m∆2(∆x + R) — ma = -k∆x – k(R – Ro) + m∆2∆x + m∆2R (IV) — substituindo (I) em (IV) — ma = -k∆x – k(R – Ro) + 2∆x + k(R – Ro) — fazendo os cancelamentos e isolando a — a= ( – k/m + w2).∆x — a= – (k/m –w2).∆x (V) — a propriedade fundamental de um MHS diz que a aceleração é diretamente proporcional à elongação (∆x) — a constante de proporcionalidade é o oposto do quadrado da pulsação do movimento oscilatório (∆osc) — a= – w2osc.∆x — a= – 2(∆f)2.∆x (VI) — igualando (V) com (VI) — 4∆2f2=k/m – w2 — f2=k/4π2m – 1/4π2.w2 — assim, o quadrado da frequência do MHS depende linearmente do quadrado da velocidade angular — R- D
17- Relação fundamental do MHS — a= – w2.x — quando t=1/3s — x=0,3cosπt=0,3cosπ.1/3 — x=0,3cosπ/3=0,3.1/2 — x=0,15m — x=0,3c0swt — w=π — a=-w2.x= – π2.0,15 — π2=10 — a=1,5m/s2 — lei fundamental da dinâmica — FR=ma — FR=0,5.1,5 — FR=0,75N — R- A
18- a) Observe na figura abaixo, as posições ocupadas pela criança na roda gigante nos instantes t=0, t=60s, t=120s, t=180s e t=240s,
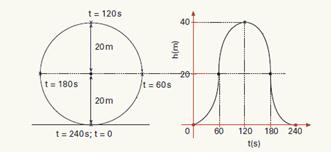
e o gráfico da altura da criança em função do tempo equivale a um MHS de amplitude a=20m, com a origem no ponto h=20m..
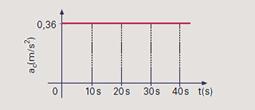
b) Supondo que o carrossel efetue uma volta completa em 20s, ou seja, T=20s — velocidade escalar — v=2πr/T=2.(3).4/20 —
v=1,2m/s — ac=V2/R=1,44/4=0,36ms2 — ac=0,36m/s2 — o gráfico pedido está representado abaixo:
19-
Como as forças dissipativas são desprezíveis, a energia mecânica é sempre constante no MHS e vale Em= kA2/2 ou Em=Ec + Ep ou Em=kx2/2 + m.v2/2 — Em=k.A2/2 — 0,4=20.A2/2 — A2=8,8/20 — A=√(4.10-2)=2.10-1m — A=0,2m — R- B.