Resolução dos exercícios sobre queda livre vertical
Resolução dos exercícios sobre queda livre vertical
01– Como a resistência do ar é desprezada eles caem com a mesma aceleração que é a da gravidade e consequentemente suas velocidades, em cada instante, serão sempre as mesma, independente das massas e consequentemente dos pesos — R- B
02- V=28m/s — Vo=0 — Torricelli — V2= Vo2 + 2.g.ΔS — 282=02 + 2.9,8.ΔS — ΔS=784/19,6 — H=40m — R- A
03- S= gt2/2=5.16 — S=80m — R- C
04- Segundo toco B no instante 1s caiu — SB=gt2/2=5.1=5m — como o primeiro toco partiu 1s antes, quando t=1s para B, será 2s para A — SA = 5tA2=5.22=20m — ΔS=20 – 5=15m — R- C
05- V2=Vo2 + 2.g.h — V2 = 02 + 2.10.500 — V=100ms — R- C
06- Chegam ao solo com a mesma velocidade — R- C
07- a) Como o balão se desloca horizontalmente, sua velocidade vertical inicial é nula — S=gt2/2 — 80=5t2 — t=4s
b) Corresponde à distância horizontal que o balão percorre em 4s com velocidade constante de 6m/s — V=d/t — 6=d/4 — d=24m
08- I- Correta – 5m/s2 significa 5(ms)/s, ou seja, variação de velocidade de 5ms em cada 1s
II – Falsa – a cada segundo o deslocamento vai aumentando, pois a velocidade é cada vez maior.
III – Falsa – segundo o enunciado a aceleração é constante e vale 5m/s2
IV – Verdadeira – V=Vo + g.t= 0 + 5.8 — V=40m/s
R- D
09- Tempo que a pedra demora para cair h=7,2m — S=gt2/2 — 7,2=5t2 — t=1,2s — nesse tempo o carro com velocidade constante de 120km/h=33,4m/s o carro se deslocou — V=ΔS/Δt — 33,4= ΔS/1,2 — ΔS=40,08m — R- C
10- a)Corpo que é abandonado da altura H e demora T para chegar ao chão — H=10T2/2 — corpo que é abandonado da altura H/4 e que demora (T – 3)s para chegar ao chão — H/4=10.(T – 3)2/2 — dividindo membro a membro — T2/(T – 3)2 =4 — T/T – 3 =2 — T=6s
b) H=10T2/2=10.36/2 — H=180m
11- A velocidade inicial de descida (Vo) do objeto é a mesma que do helicóptero — S=Vo.t + g.t2/2 — 100=Vo.4 + 10.16/2 —
Vo=20/4 — Vo=5m/sX3,6=18km/h — R- D
12- a) Nesse caso, pela equação observava-se que a origem da trajetória está no solo e que ela é orientada para cima —
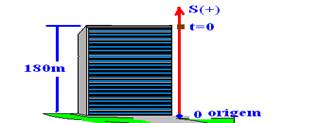
comparando S=So + gt2/2 com S=180 – 5t2 — So=180m ou, substituindo t=0 na equação — R- 180m
a) A altura do prédio é dada pela função em t = 0, ou seja, 180 metros.
b) A pedra atinge o solo quando S=0 — 0= 180 – 5t2, isto é, 5t2 = 180 ==> t2 = 180/5 = 36, de onde vem que t = 6 s.
13- S=gt2/2 — 11=4t2/2 — t=√5,5=2,3s — R- A
14- R- A (veja teoria)
15-

R- C
16-
Colocando a origem no ponto de lançamento e orientando a trajetória para baixo, 1uando ele se encontra a 80m do solo, sua posição é S=130 – 80=50m
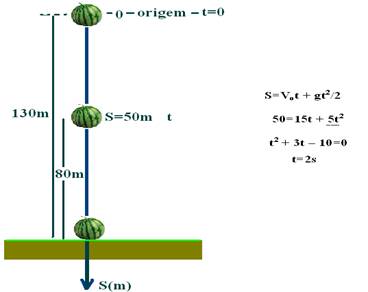
R- t=2s
17- a) A aceleração de queda da plataforma é a aceleração da gravidade local fornecida pelo exercício, g=10m/2
b) Velocidade da plataforma quando se encontra 30m acima do solo, ou seja, após ter percorrido ΔS=75 – 30=45m — Torricelli — V2=Vo2 + 2.g.ΔS — V2=02 + 2.10.45 — V=30m/s
c) Imobilizada (freando – a<0) — V=0 — Torricelli — V2=Vo2 + 2.(-a).h — 02=302 – 2a.30 — a=900/60 — a=15m/s2
18- V2=Vo2 + 2.g.h=02 + 2.10.5 — V=10m/sX3,6=36km/h — R- A
19- Proporções de Galileu para queda livre com Vo=0 e desprezando-se a resistência do ar:
Para intervalos de tempos iguais e consecutivos, um corpo em queda livre percorre distâncias cada vez maiores, na proporção dos
ímpares consecutivos: no primeiro segundo, o móvel cai uma distância d; no segundo seguinte, percorre 3d; no terceiro segundo,
5d, e assim por diante.
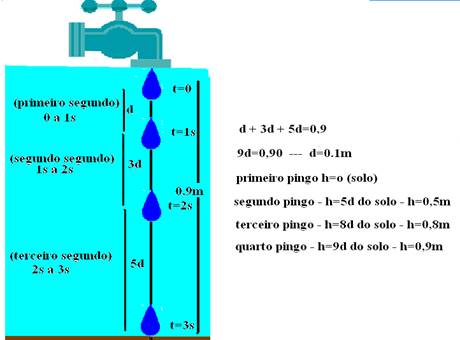
a) falsa – velocidade é diferente de aceleração
b) falsa – estava a 0,50m do solo
c) falsa – estava a 0,80m do solo
d) Verdadeira – Ec=mV2/2 — quanto maior a velocidade, maior será a energia cinética — o terceiro pingo tem maior velocidade que o quarto pingo, que, nesse instante está abandonando a torneira.
R- D
20- a) Torricelli — V2=Vo2 + 2.g.h=02 + 2.10.1 — V=√20 — V=4,47m/s
b) Como o tempo de queda é o mesmo, o intervalo de tempo entre as batidas de duas gotas consecutivas é o mesmo intervalo de tempo compreendido entre as saídas de duas gotas consecutivas da torneira. Se saem 3 gotas em cada 60s, tem-se que, entre a 1a e a 2a (20s); entre a 2a e a 3a (20s) e entre a 3a e a 4a (20s) e assim, a partir do instante em que uma bate no solo, depois de 20s chega a outra ao solo — R- 20s
21- Objeto M, solto do repouso Vo=0 — SM=H=gtM2/2 — H=5tM2 — objeto N arremessado para baixo com velocidade inicial Vo=80m/s — S=Vo.tN + gtN2/2 — S=80tN+ 5tN2 — como M partiu 4s antes — tM – tN=4 — tM=tN + 4 — H=15.(tN + 4)2 — H=5(tN2 + 8tN + 16) — H=5tN2 + 40tN + 80 — se encontram no solo — H = S — 5tN2 + 40tN + 80 = 80tN + 5tN2 — 40tN + 80 = 80tN — tN=2s — substituindo tN=2s em S=H=80tN + 5tN2=80.2 + 5.4=160 + 20 — H=180m — R- D
22-
Cálculo da velocidade V1 após a 1a colisão — V12= 02 + 2.g.hO — V1=√2gho I — V2 – velocidade logo após a 1a colisão — f=V2/V1 — V2=f.√2gho (velocidade de subida que é igual em módulo à velocidade V3 com que ela retorna) — V2=f.√2gho —
F=V3/V2 — V3=f.f.√2gho — V3=f2.√2gho — analogamente após a 3a colisão — V4=f3.√2gho — assim, após a 3a colisão ela é
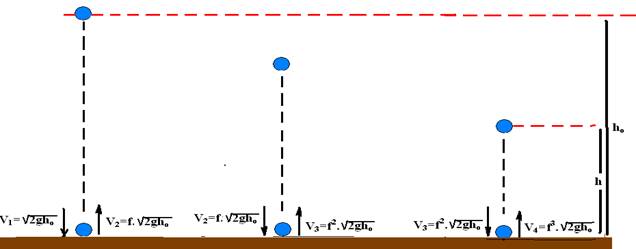
lançada para cima com velocidade V4=f3.√2gho atingindo uma altura h, quando V=0 — V2= V42 – 2gh — 0 = (f3.√2gho)2 – 2.g.h — f6.2gho = 2gh — h=f6.ho
23- I – Falsa — a velocidade aumenta de 10ms em cada 1s
II – Falsa — h=gt2/2 — h=5.12 — h=5m
III – Verdadeira — V=gt=10.2 — V=20m/s
R- B
24- Tempo de queda do saco — h=gt2/2 — 500=5t2 — t=10s — Nesse tempo o avião deve se deslocar ΔS com velocidade constante de V=144km/h/3,6=40m/s — V=ΔS/Δt — 40= ΔS/10 — ΔS=400m — R- D
25- A velocidade é a mesma independente da massa — Pmelancia=mmelancia.g=5g — Pmaçã=mmaçã.g=0,05.g — R- C
26- H=gt2/2 — 20=5t2 — t=2s — V=gt=10.2=20m/s — R- B
27- Observe a figura abaixo onde L é a distância horizontal entre a mancha e o dublê no instante do salto — cálculo do tempo de
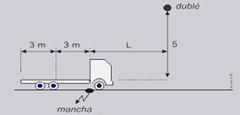
queda do dublê — h=gt2/2 — 5=10t2/2 t2=1 — t=1s — a velocidade ideal Vi=ΔS/Δt=(L + 3)/1 — Vi=L + 3 — velocidade mínima — Vm= ΔS/Δt=L/1 — Vmin=L — velocidade máxima — Vmax= ΔS/Δt=(L + 6)/1 — Vmax=L + 6 — diferenças —
V1=Vi – Vmin= (L + 3) – L — V1=3m/s — V2= Vmax – Vi=(L + 6) – (L + 3) — V2=3m/s
R- B
28- Dados: ho = 20 m; g = 10 m/s2; vo = 0.
A Figura abaixo ilustra a situação descrita no enunciado — desprezando a resistência do ar, trata-se de uma queda livre, que é
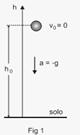
um movimento uniformemente variado — equação da altura em função do tempo — h=ho + Vot + gt22 — h=20 – 5t2 — o
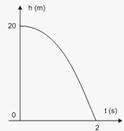
gráfico dessa função é um arco de parábola com concavidade para baixo — quando h=0 — 0=20 – 5t2 — t=√4 — t=2s
R- D
29- Dados: g = 10 m/s2 ; t = 6 s — para a queda livre — h=gt2/2=10.62/2 — h=180m — R- A
30- Aplicando a equação de Torricelli — V2=Vo + 2.g.h — Vo=0 — V2=2gh — Ec=mV2/2 — EcTerra=m.(2gTerra.h) — EcLua=m.(2gLua.h) — como a gravidade na superfície da Terra é maior que a gravidade na superfície da Lua, a energia cinética na superfície da Terra é maior que a energia cinética na superfície da Lua — em relação à queda livre — h=gt2/2 — t=√2h/g — como gLua<gTerra, o tempo de queda na Lua é maior do que na Terra — R- A
31-
Cálculo da distância total (∆S) percorrida — ∆S=5 + 15 + 25 + 35=80m —∆S=80m — trata-se de uma queda livre com So=0 e Vo=0 (abandonado) — V=Vo + gt=0 + 10.4 — V=40m/s.
32-
A. Falsa — a energia mecânica diminui se houver atrito com o ar ou permanece a mesma se não houver atrito com o ar.
B. Falsa — a velocidade da régua aumenta a medida que ela desce.
C. Falsa — a aceleração da régua é a aceleração da gravidade que permanece constante (mesmo local).
D. Correta — a força que provoca a queda da régua é a força peso, que a faz descer com aceleração constante que é a da gravidade g, pois P=m.g.
E. Falsa — veja (B).
R- D.
