Efeito Fotoelétrico
Efeito Fotoelétrico
Introdução à Física Moderna
A Física clássica, das leis que regem os a Cinemática, a Dinâmica, a Óptica, a Ondulatória, o Eletromagnetismo, etc. que explicam o funcionamento dos nossos aparelhos elétricos e eletrônicos, dos carros, trens, e que são partes importantes e relevantes da Física, continua sendo válida, precisa, e até sendo aperfeiçoada.
No entanto, só é aplicável dentro de determinados limites.
Mas, quando você quer resolver problemas que envolvam ordens de grandeza na descrição da natureza, de ordens muito pequenas (micro) até ordens muito elevadas (macro) deve-se recorrer à física moderna cuja evolução, a partir do século XIX e início de XX se tornou vertiginosa, teoricamente e tecnologicamente.
Graças Física Moderna surgiram inúmeras descobertas científicas em todos os ramos da física, desde a medicina até a física atômica e nuclear, que estão sendo utilizadas no benefício da humanidade.
Algumas, dentre as inúmeras: Telefones celulares, micro computadores, câmeras digitais,
transmissão de sons e imagens em tempo real através de satélites artificiais, células fotoelétricas, raios X, ultra-sons, ressonância magnética, cirurgias a laser, injeção eletrônica nos carros, etc.
Devido ao fato de a Física Moderna estar muito relacionada com o funcionamento de muitos aparelhos do cotidiano da maioria das pessoas, a introdução do assunto no ensino médio é muito interessante, e seu conteúdo está sendo exigido cada vez mais nos principais vestibulares do país.
Resumo histórico da Física Moderna
A Física Moderna começou a ser pesquisada e desenvolvida no final do século XIX e início do século XX, principalmente nas três primeiras décadas do século passado e principalmente através da teoria da relatividade proposta por Albert Einstein e a teoria
quântica proposta por Max Planck.
Toda essa teoria já resultou, no final do século XX, em toda tecnologia conhecida hoje.
Atualmente a tentativa é unificar a teoria da relatividade com a teoria da mecânica quântica na tendência de explicar o Universo, do extremamente grande ao infinitamente pequeno.
Ondas eletromagnéticas – Definição e Histórico
Surgem quando um condutor que é percorrido por uma corrente elétrica origina ao seu redor um campo magnético que só existe enquanto houver corrente.
Assim, um campo magnético deve gerar também um campo elétrico. Quando um desses campos varia, o outro também sofre variação. Baseado nesse fenômeno, James Clerk Maxwell (1831-1879) concluiu que, se um campo elétrico variável faz surgir um campo magnético variável, este deve fazer surgir um outro campo elétrico variável e assim por diante. 
Esse encadeamento, através do espaço de campos elétricos e magnéticos constitui as ondas eletromagnéticas.
Através de seus estudos teóricos para a fundamentação do eletromagnetismo Maxwell conseguiu obter o valor da velocidade da luz (onda eletromagnética) no vácuo como sendo de v =c = 3,0.108m/s.
Somente oito anos depois da morte de Maxwell, em 1887, Heinrich Rudolf Hertz (1857-1894), em uma série de experimentos conseguiu produzir essas ondas eletromagnéticas, (também chamadas de ondas hertzianas em sua homenagem) e, confirmando as previsões teóricas de Maxwell, permitiu o nascimento de uma nova era tecnológica: a da transmissão de informação através de ondas eletromagnéticas.
A partir daí, o desenvolvimento das tecnologias permitiu tirar delas todos os imensos benefícios que hoje desfrutamos e que iremos desfrutar.
Efeito fotoelétrico
Heinrich Rudolf Hertz, em 1887, detectou e gerou em laboratório, em uma série de experiências que,
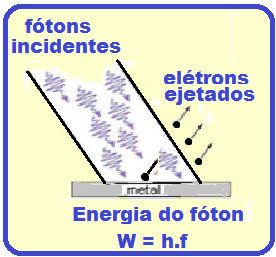
experiências que, quando a luz (onda eletromagnética, radiação eletromagnética) de freqüência suficientemente alta incide sobre a superfície de um metal, ela pode retirar elétrons do mesmo.
Esse fenômeno ficou conhecido como efeito fotoelétrico.
Experiências que ilustram o efeito fotoelétrico
A figura abaixo ilustra uma experiência simples que permite observar o efeito fotoelétrico.
No interior da ampola de vidro existe vácuo e entre as placas A e B existe uma diferença de potencial variável U = VA – VB.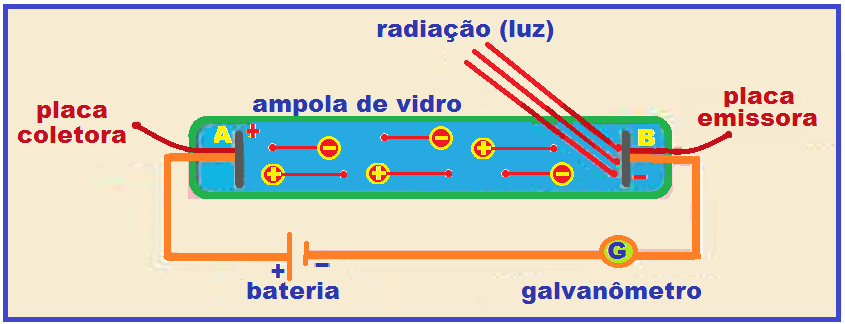 
Sem a incidência de radiação
eletromagnética, não existe corrente elétrica no circuito.
Com a incidência de radiação eletromagnética na placa B, mantida num potencial elétrico menor que a placa A, surge uma corrente elétrica (movimento ordenado de elétrons que são extraídos da placa B), e que é medida pelo galvanômetro (amperímetro).
Outra experiência simples que demonstra a existência do efeito fotoelétrico 
Quando um bastão eletrizado com cargas, por exemplo, negativas é encostado na esfera do eletroscópio que estava neutro (hastes fechadas), o bastão transfere cargas ao eletroscópio, eletrizando-o e abrindo as hastes de determinado ângulo.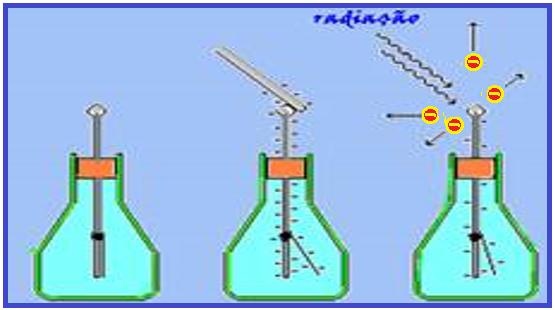
Em seguida, se você fizer incidir radiação eletromagnética (por exemplo, luz) sobre a esfera do eletroscópio, o ângulo entre as duas hastes diminui, assinalando uma diminuição da carga em excesso no eletroscópio devido à emissão de elétrons causada pelo efeito fotoelétrico.
Explicação do Efeito Fotoelétrico
Foi Albert Einstein que explicou corretamente o efeito fotoelétrico em 1921, recebendo por isso o prêmio Nobel da Física.
Segundo Einstein a energia de qualquer radiação luminosa (inclusive luz) não se espalha uniforme e continuamente pelo espaço mas, sim, concentrada em pequenos “pacotes”que carregam uma quantidade bem definida de energia.
Cada um desses pacotes é denominado quantum de energia e esse modelo construído por Einstein recebeu o nome de teoria dos quanta.
Quanta, em latim é plural de quantum, que significa “quantidade”.
Esses quanta de energia radiante foram denominados de fótons.
O fóton, como qualquer partícula, possui uma certa energia (W), e a relação energia (W) e frequência (f), é proporcional e está relacionada por uma constante, a constante de Planck (h).
Observações:
elétron-volt (eV) e joule (J) são unidades de energia e a relação entre elas é 1 eV = 1,6.10-19 J.
A equação W = h.f é usada para calcular a energia de um fóton quando é dada a freqüência. Nessa equação a energia W é calculada em joule (J) quando o valor de h é substituído por h = 6,63.
10-34 J.s e, em elétron-volt (eV) quando a constante de Planck h é substituída por h = 4,14.10-15 eV.
A velocidade de uma onda (partícula, fóton) é calculada por v = c = λf 
isolando a frequência f = v/λ e substituindo na equação da energia (W = hf) você irá encontrar uma nova expressão para o cálculo da energia (W) em função do comprimento de onda (λ
Condições para que ocorra o efeito fotoelétrico
Como já vimos, o efeito fotoelétrico é interpretado como a absorção de um fóton pela matéria, levando à ejeção de um elétron.
Os elétrons que giram à volta do núcleo são aí mantidos por forças de atração.
Se eles receberem energia suficiente (energia mínima de extração), eles abandonarão as suas órbitas.
O efeito fotoelétrico só surge se o metal receber um feixe de radiação com energia superior à energia mínima de remoção dos elétrons do metal, provocando a sua saída das órbitas o que pode ocorrer sem energia cinética (se a energia da radiação for igual à energia de remoção) ou com energia cinética,( se a energia da radiação exceder a energia de remoção dos elétrons).
Essa energia mínima (Wmin) para extrair um elétron da placa metálica é denominada função trabalho e está relacionada com o tipo de metal utilizado.
Se a energia do fóton que incide (W = h.f) for maior que a função trabalho (Wmin) a energia em excesso será energia cinética (Ec), de modo que Wmin = W – Ec Wmin = h.f – Ec
(equação fotoelétrica de Einstein).
Da equação W = h.f fo = W/h fo é a frequência mínima (frequência de corte) a partir da qual os elétrons são extraídos do metal.
Assim, nenhum elétron é emitido pelo metal enquanto a frequência da luz (fótons) incidente não ultrapassar um certo limite de frequência, denominada frequência de corte (fo).
Gráfico da energia cinética do elétron extraído em função da frequência da radiação do (fóton, luz) incidente.
A figura ao lado mostra o gráfico da energia cinética do elétron extraído em função da frequência da radiação do fóton (luz) incidente, para uma mesma placa metálica (célula fotoelétrica).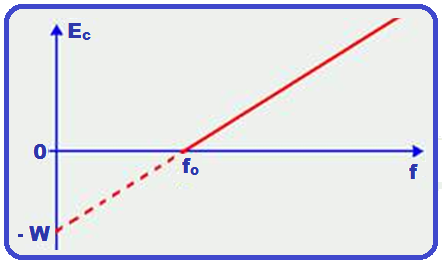
fo é a frequência mínima (frequência de corte) necessária para produzir o efeito fotoelétrico.
Se f = fo o elétron é liberado, mas sua energia cinética é nula.
Para frequências inferiores a fo o fenômeno não ocorre (nenhum elétron é liberado).
Porém, para valores superiores a fo, o número de elétrons arrancados é diretamente proporcional à intensidade da radiação eletromagnética incidente, ou seja, aumentando a intensidade “número” da radiação incidente no metal, aumenta-se o nível energético dos fótons incidentes, aumentando assim o número de elétrons arrancados.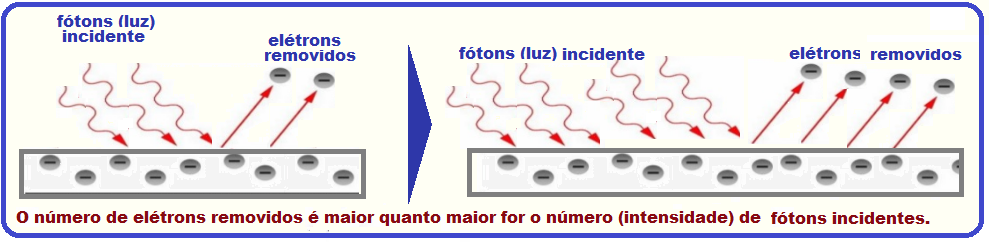
Observe no gráfico que, para a mesma placa (mesma frerquência de corte fo), à medida que a freqüência da radiação incidente aumenta, a energia cinética dos elétrons emitidos também aumenta.
Mas, para a mesma freqüência f, a energia cinética dos elétrons emitidos é sempre a mesma, pois, Ec = hf – W = h.f – h.fo = constante1 – constante2 = constante.
Aumentando-se a intensidade da radiação incidente, isto é, aumentando-se o número de fótons incidentes, aumenta o número de elétrons emitidos (figura acima) sem alterar a energia cinética máxima deles.
Abaixo de fo não há emissão de elétrons, independentemente da intensidade da radiação incidente.
Algumas das muitas utilidades práticas do efeito fotoelétrico
Dualidade da luz
Quando a luz interage com a matéria através de absorção, emissão, choques, etc., ela se comporta como partícula, mas para os fenômenos referentes à sua propagação, reflexão, refração, interferência, etc., ela se comporta como onda.
O físico francês Louis de Broglie apresentou, em 1924, a seguinte hipótese que, depois, em 1927 foi comprovada experimentalmente: “partículas também possuem propriedades ondulatórias”.
Das equações E = W = m.c2 c velocidade da luz no vácuo W = h.f c = λf f = c/λ
mc2 = hf mc2 = h(c/λ) λ = h/mc mc = Q quantidade de movimento λ = h/Q
Nessa expressão λ = h/Q , como h é constante, a quantidade de movimento Q = mV evidencia o caráter corpuscular da luz (m é massa da particula) enquanto que o comprimento de onda λ evidencia seu caráter ondulatório.
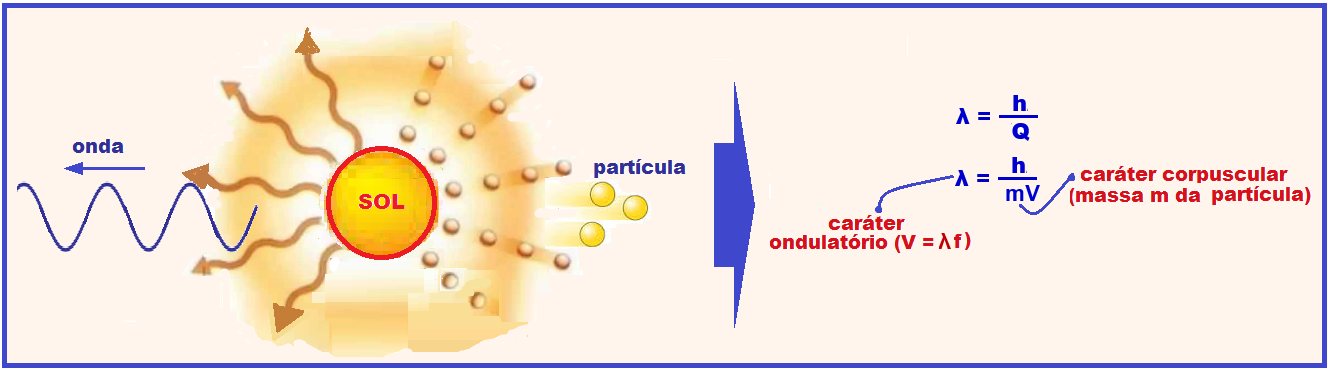
As naturezas ondulatória e corpuscular da luz são complementares e não antagônicas
O que você deve saber, informações e dicas
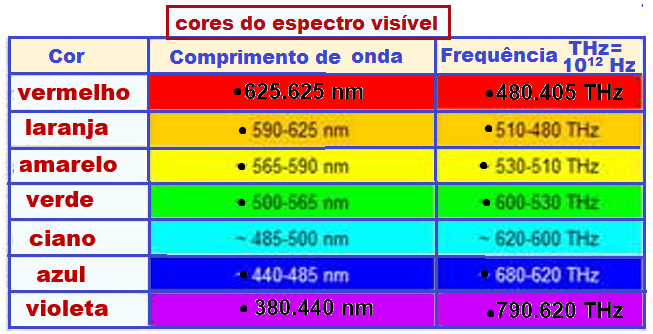
Observe na tabela ao lado que a freqüência e consequentemente o nível de energia dos fótons incidentes aumenta do vermelho para o violeta.
A equação W = h.f é usada para calcular a energia de um fóton quando é dada a freqüência. Nessa equação a energia W é calculada em joule (J) quando o valor de h é substituído por h = 6,63.
10-34 J.s e, em elétron-volt (eV) quando a constante de Planck h é substituída por h = 4,14.10-15 eV.
elétron-volt (eV) e joule (J) são unidades de energia e a relação entre elas é 1 eV = 1,6.10-19 J.
A figura ao lado mostra o gráfico da energia cinética do elétron extraído em função da frequência da radiação do fóton (luz) incidente, para uma mesma placa metálica (célula fotoelétrica).
fo é a frequência mínima (frequência de corte) necessária para produzir o efeito fotoelétrico.
Se f = fo o elétron é liberado, mas sua energia cinética é nula.
Para frequências inferiores a fo o fenômeno não ocorre (nenhum elétron é liberado).
Os elétrons são emitidos imediatamente. Não existe atraso de tempo entre a incidência da luz e a emissão dos elétrons.
Para valores superiores a fo (frequência de corte), o número de elétrons arrancados é diretamente proporcional à intensidade da radiação eletromagnética incidente, ou seja, aumentando a intensidade “número” da radiação incidente no metal, aumenta-se o nível energético dos fótons incidentes, aumentando assim o número de elétrons arrancados.
Da equação W = h.f fo = W/h fo é a frequência mínima (frequência de corte) a partir da qual os elétrons são extraídos do metal.
Assim, nenhum elétron é emitido pelo metal enquanto a frequência da luz (fótons) incidente não ultrapassar um certo limite de frequência, denominada frequência de corte (fo).
Observe no gráfico que, para a mesma placa (mesma frerquência de corte fo), à medida que a freqüência da radiação incidente aumenta, a energia cinética dos elétrons emitidos também aumenta.
Mas, para a mesma freqüência f, a energia cinética dos elétrons emitidos é sempre a mesma, pois, Ec = hf – W = h.f – h.fo = constante1 – constante2 = constante.
Aumentando-se a intensidade da radiação incidente, isto é, aumentando-se o número de fótons incidentes, aumenta o número de elétrons emitidos (figura acima) sem alterar a energia cinética máxima deles.
Abaixo de fo não há emissão de elétrons, independentemente da intensidade da radiação incidente.
A emissão e a energia dos elétrons arrancados dependem da freqüência e não da intensidade da
radiação eletromagnética incidente.
A energia cinética máxima é fornecida pela expressão Ec = e.Vo (e carga de 1 elétron e Vo potencial de corte)
O potencial de corte é o mesmo qualquer que seja a intensidade da radiação eletromagnética incidente.
A energia cinética do elétron emitido é dada pela equação Ec = mv²/2 = hf – W, em que o termo hf é a energia cedida ao elétron pela luz, sendo h a constante de Planck e f a frequência da luz incidente.
O termo W é a energia que o elétron tem que adquirir para poder sair do material, e é chamado função trabalho do metal.
Sendo c a velocidade da luz no vácuo (c=3,0.108m/s), λ o comprimento de onda da radiação (luz) do fóton incidente e f a freqüência da onda (luz, elétrons) emitida, tem-se c = λf W = hf W = h.(c/λ).
Observe na expressão W = h.(c/λ) que, como h e C são constantes, a energia do fóton (quantum) necessária para liberar elétrons (emitir luz) é inversamente proporcional ao comprimento de onda.
Assim, como, por exemplo, a cor vermelha tem baixa freqüência (ou grande comprimento de onda λ), os fótons de luz vermelha têm baixa energia e não conseguem arrancar elétrons.
Mas, a cor azul (pequeno comprimento de onda e grande frequência), possui mais energia e consegue arrancar elétrons.
A luz tem caráter dual: Quando a luz interage com a matéria através de absorção, emissão, choques, etc., ela se comporta como partícula, mas para os fenômenos referentes à sua propagação, reflexão, refração, interferência, etc., ela se comporta como onda.
“De acordo com a teoria formulada em 1900 pelo físico alemão Max Planck, a matéria emite ou
absorve energia eletromagnética de maneira descontínua emitindo ou absorvendo fótons, cuja energia é proporcional à frequência da radiação eletromagnética envolvida nessa troca de energia.”
Alguns exercícios interessantes a que convém conferir as resoluções
01-(UFRN) Bárbara ficou encantada com a maneira de Natasha explicar a dualidade onda-partícula, apresentada nos textos de Física Moderna.
Natasha fez uma analogia com o processo de percepção de imagens, apresentando uma explicação baseada numa figura muito utilizada pelos psicólogos da Gestalt.
Seus esclarecimentos e a figura ilustrativa são reproduzidos a seguir:
Figura citada por Natasha, na qual dois perfis formam um cálice e vice-versa.
A minha imagem preferida sobre o comportamento dual da luz é o desenho de um cálice feito por dois perfis.
Qual a realidade que percebemos na figura? Podemos ver um cálice ou dois perfis, dependendo de quem consideramos como figura e qual consideraremos como fundo, mas não podemos ver ambos simultaneamente.
É um exemplo perfeito de realidade criada pelo observador, em que nós decidimos o que vamos observar.
A luz se comporta de forma análoga, pois, dependendo do tipo de experiência (“fundo”), revela sua natureza de onda ou sua natureza de partícula, sempre escondendo uma quando a outra é mostrada.
Diante das explicações acima, é correto afirmar que Natasha estava ilustrando, com o comportamento da luz, o que os físicos chamam de princípio da:
a) incerteza de Heisenberg.
b) complementaridade de Bohr.
c) superposição.
d) relatividade.
Resolução:
As naturezas ondulatória e corpuscular da luz são complementares e não antagônicas R- B
02-(UFMG-MG) Em alguns laboratórios de pesquisa, são produzidas antipartículas de partículas fundamentais da natureza. Cite-se, como exemplo, a antipartícula do elétron – o pósitron -, que tem a mesma massa que o elétron e carga de mesmo módulo, porém positiva. Quando um pósitron e um elétron interagem, ambos podem desaparecer, produzindo dois fótons de mesma energia.
Esse fenômeno é chamado de aniquilação. Com base nessas informações,
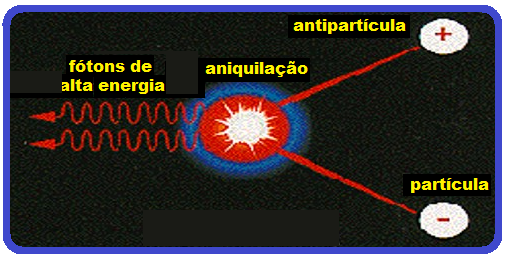
a) Explique o que acontece com a massa do elétron e com a do pósitron no processo de aniquilação.
Considere que tanto o elétron quanto o pósitron estão em repouso.
b) Calcule a frequência dos fótons produzidos no processo de aniquilação.
Dado que a massa do elétron é 9,1.10-31kg, a velocidade da luz no vácuo é 3.108m/s e a constante de Planck é 6,6.10-34J.s.
Resolução:
a) As energias dos fótons que surgiram foram obtidas através das massas do elétron e do pósitron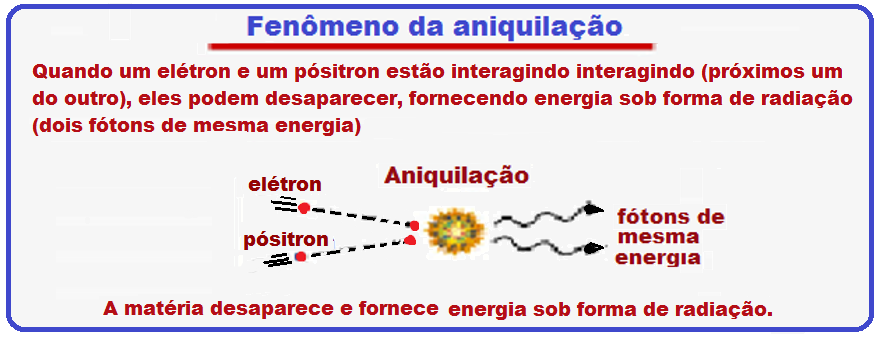
que desapareceram no processo de aniquilação.
Essa transformação de massa em energia é explicada pela teoria da relatividade de Einstein na equação E = mc2, onde m é a quantidade de massas convertidas em energia e c a velocidade da luz no vácuo, de valor c = 3,0.108 ms.
b) A energia de um fóton (E) e a sua frequência (f) estão relacionadas pela expressão E = h . f, em que h é a constante de Planck.
Igualando as energias dos dois fótons ao equivalente em energia das massas das partículas aniquiladas (elétron e pósitron) Efótons = Emassas equivalentes 2.(h.f) = 2.Melétron .c2
6,6.10-34.f = 9,1.10-31.(3.108)2 f = 1,2.1020 Hz.
03-(UFPE-PE)
O césio metálico tem uma função trabalho (potencial de superfície) de 1,8 eV.
Qual a energia cinética máxima dos elétrons, em eV, que escapam da superfície do metal quando ele é iluminado com luz ultravioleta de comprimento de onda igual a 327 nm? Considere: 1eV=1,6.10-19J; h=6,63.10-34J.s e C=3,0.108m/s
Resolução:
Ecin.máx .= h.f – W V = c = λf f = C/λ Ecin.máx .= h.(C/λ) – W W = 6,63.1034.(3.108/327. 10-9) – 1,8.1,6.10-19 Ecin.máx.=3,8 – 1,8 Ecin.máx.=2,0 eV.
Resolução:
a) Dados: m1 = m2 = 2 g = 2.10-3 kg; c = 3.108 m/s a massa a ser convertida em energia é m = m1 + m2 = 4.10-3 kg da equação de Einstein, a energia liberada na aniquilação é Elib = mc2 Elib = 4.10-3.(3.108)2 Elib = 4.10-3.9.1016 Elib = 3,6.1014 J.
b) Dados população de 1 milhão de habitantes N = 106 habitantes consumo médio 100 kWh/habitante.mês.
Lembrando que 1 kWh = 3,6.106 J, a potência consumida mensalmente pela cidade é Potcons = 100.106.3,6.106 = 360.1012 Potcons=3,6.1014 J/mês Potcons = Elib/Δt 3,6.1014 = 3,6.1014/Δt
Δt = 1 mês.