Associação de molas
Associação de molas
Duas molas 1 e 2 tem constantes elásticas k1 e k2, respectivamente. Podemos associá-las em série ou em paralelo. Em cada uma dessas associações podemossubstituir as duas molas por uma única, que produza o mesmo efeito e que chamamos de mola equivalente de constante elástica ke.
Associação em paralelo
Nesse caso a deformação x sofrida por cada uma das molas é a mesma.
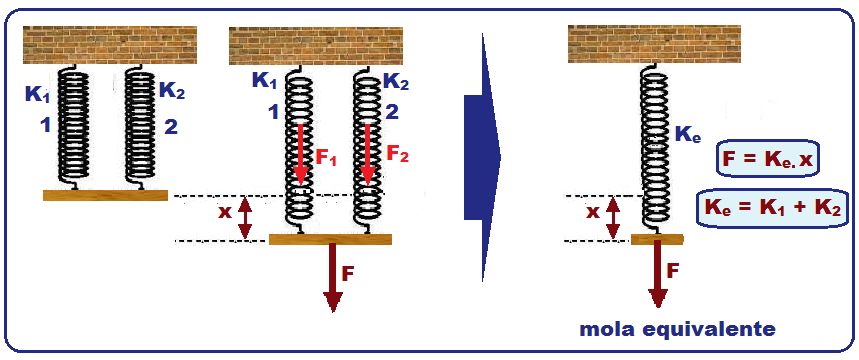
Quando deformadas de x, a mola 1 fica sujeita a uma força F1 = k1.x e a mola 2 a uma força F2 = k2.x.
A mola equivalente, quando submetida à mesma força F, sofre a mesma deformação x de modo que F = ke.x.
Observe que F = F1 + F2 
ke.x = k1.x + k2.x ke = k1 + k2.
Se você tiver n molas Ke = K1 + K2 + K3 + …. Kn.
Associação em série
Nesse caso as molas 1 e 2 estão sujeitas à mesma força F e sofrem deformações diferentes x1 e x2.
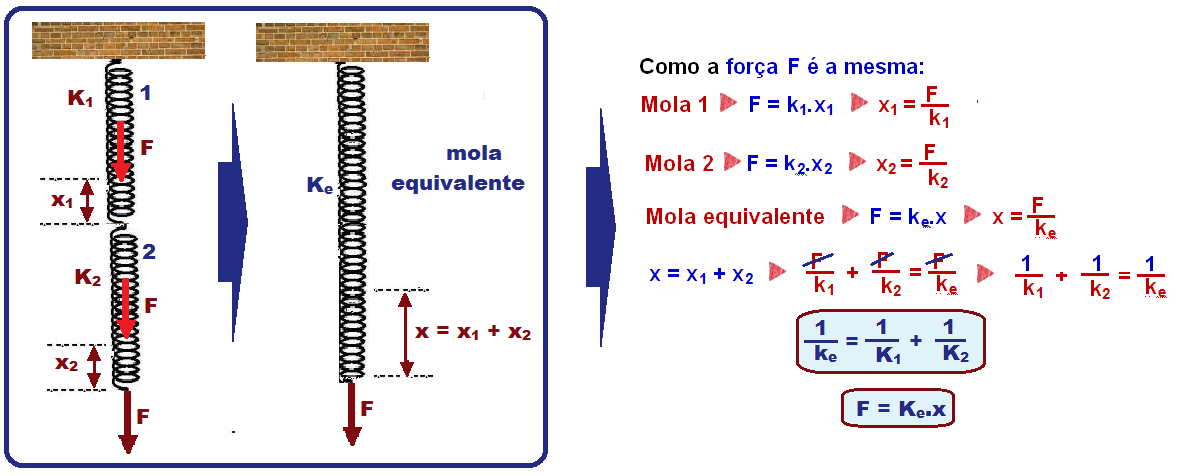
Se você tiver n molas 1/Ke = 1/K1 + 1/K2 + 1/K3 + …. 1/Kn.
O que você deve saber, informações e dicas
A constante elástica é algo que define a mola, isto é, suas características físicas (maleabilidade, maciez), constantes elásticas maiores tendem a ter uma rigidez maior.
Associação em série
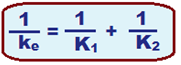
Associação em paralelo
Na associação de molas em série onde 1/ke = 1/k1 + 1/k2, o valor de ke fica bastante reduzido, sendo que a mola equivalente é menos rígida, mais deformável.
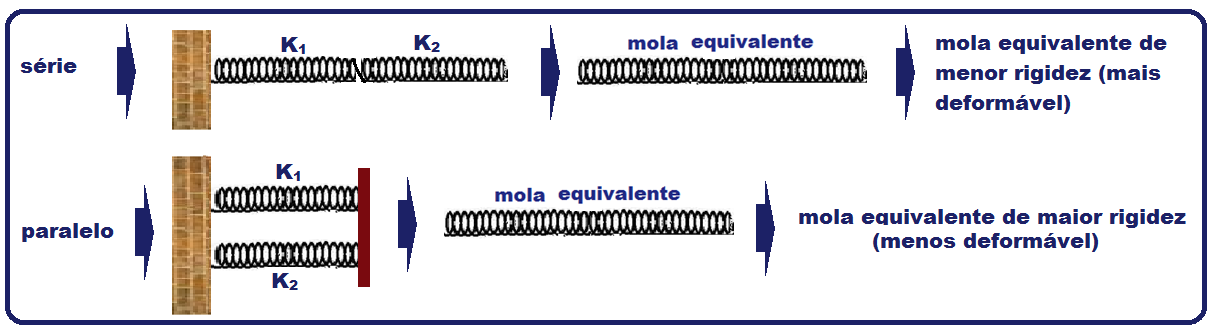
Se quisermos aumentar a rigidez da mola equivalente, torna-a menos deformável, devemos associar as molas em paralelo, onde ke = k1 + k2. É mais eficaz e ocupa menos espaço.
Você parte uma mola de constante elástica K em duas partes iguais, de modo a obter duas molas idênticas.
Cálculo da constante elástica K’ de cada pedaço que é diferente de K, pois apesar do material ser o mesmo, o número de espiras diminui:
A mola original de constante elástica K é composta das duas metades de constantes elásticas K’, associadas em série.
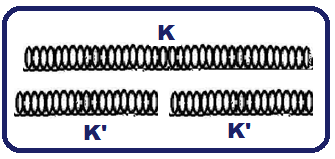
Na associação em série 1/K = 1/K’ + 1/K’ 1/K = 2/K’ K’ = 2K (a rigidez de cada metade fica o dobro da constante da mola original, tornando-as menos deformáveis).
Se você associar cada uma dessas metades de (K’ = 2K) em paralelo você obterá uma mola de
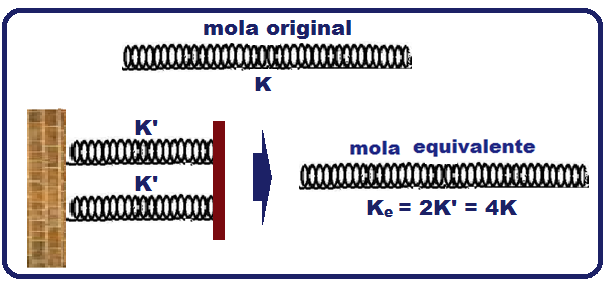
constante elástica equivalente Ke, tal que Ke = K’ + K’ = 2K + 2K Ke = 4K (a rigidez da mola equivalente da associação paralelo dessas duas metades fica quatro vezes maior que o da constante da mola original, tornando a mola equivalente menos deformável).