Força magnética sobre uma carga móvel imersa num campo magnético
Força magnética sobre uma carga móvel imersa num campo magnético
Quando uma carga elétrica que se move com velocidade 
no interior de um campo magnético 
sobre ela surge uma força de origem magnética 
( denominada força de Lorentz), com as seguintes características:
Direção e sentido de 
fornecidos pela regra da mão esquerda conforme mostrado na
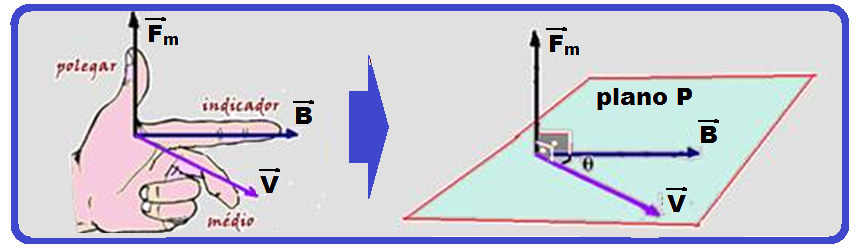
figura acima.
Observe na figura da direita que é perpendicular a e a , o que impõe a condição de que e devem pertencer a um mesmo plano.
Observe também que θ é o ângulo entre e .
Conhecendo a direção e o sentido de e de você pode, pela regra da mão esquerda, determinar a direção e o sentido da força magnética como você pode observar no esquema abaixo, onde uma carga positiva move-se com velocidade no interior de um campo magnético uniforme .
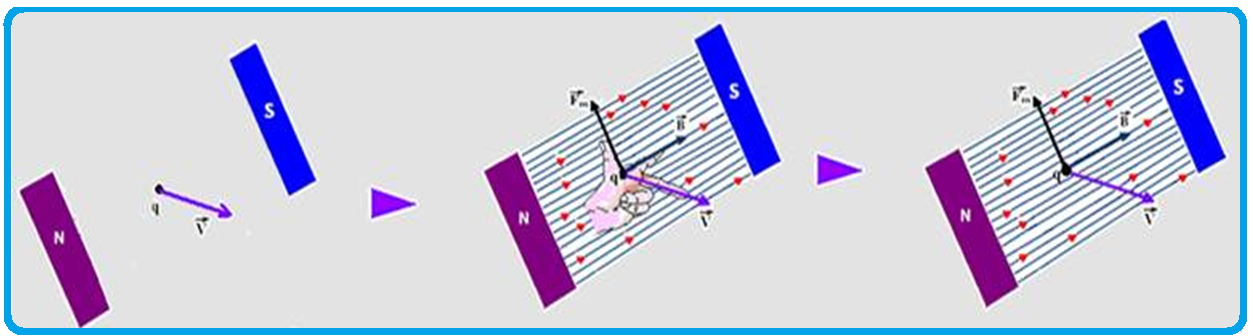
Observe que a direção e sentido das linhas de indução magnética e consequentemente de é do polo norte para o polo sul.
Adaptando o indicador e o médio nas direções de e de você determina a direção e sentido de.
Observação: Se q for negativa você deve inverter o sentido da força magnética .
O que você deve saber, informações e dicas
Como a força magnética tem sempre direção perpendicular ao vetor velocidade e como a potência de uma força é fornecida por Po = Fm.V.cosθ, então θ = 90o e cos 90o = 0 
Po = Fm.V.0 Po = 0 se a potência é nula o trabalho também será, pois Po = W/∆t 0 = W/∆t
W = 0.
O trabalho realizado pela força magnética é sempre nulo ou, a força magnética nunca realiza trabalho.
Convenção
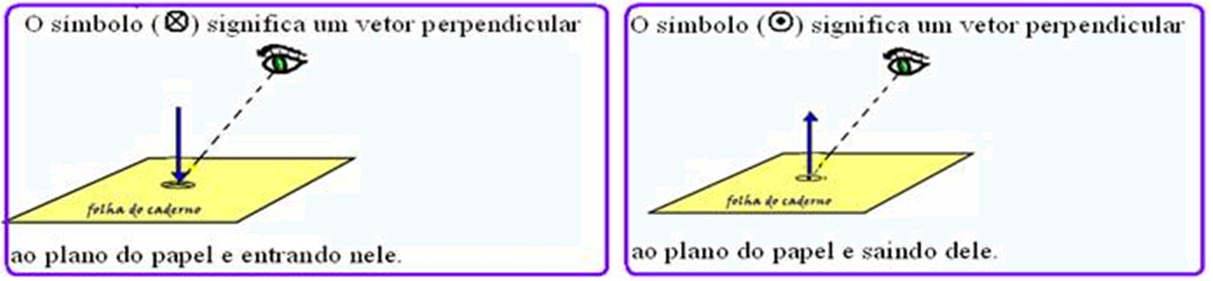
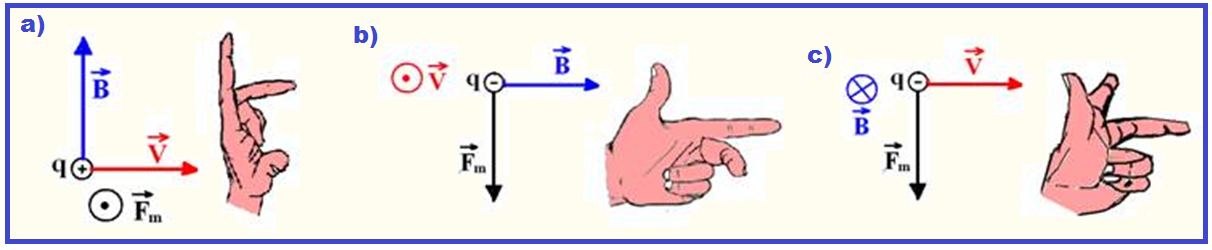
Alguns exemplos:
Nas figuras abaixo estão representadas as forças magnéticas e a disposição final da mão esquerda. Observe que nos casos b e c a força magnética tem sentido oposto ao dado pela regra da mão esquerda, pois a carga elétrica é negativa.
Força magnética sobre carga elétrica – casos particulares
Você já viu que as principais características da força magnética que atua sobre uma carga elétrica imersa num campo magnético tem as seguintes características:
Direção e sentido de fornecidos pela regra da mão esquerda conforme mostrado na figura abaixo.
Observe na figura da direita que é perpendicular a e a , o que impõe a condição de que edevem pertencer a um mesmo plano. Observe também que θ é o ângulo entre e .
Intensidade de é proporcional a q, V, B e ao senθ, obedecendo à equação:
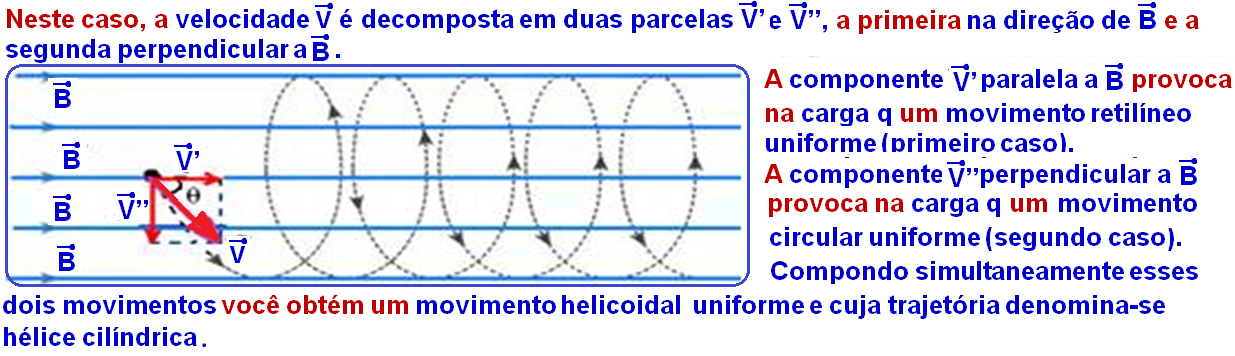
Carga em repouso (V = 0) ou lançada com velocidade paralelamente às linhas de indução de um campo magnético uniforme
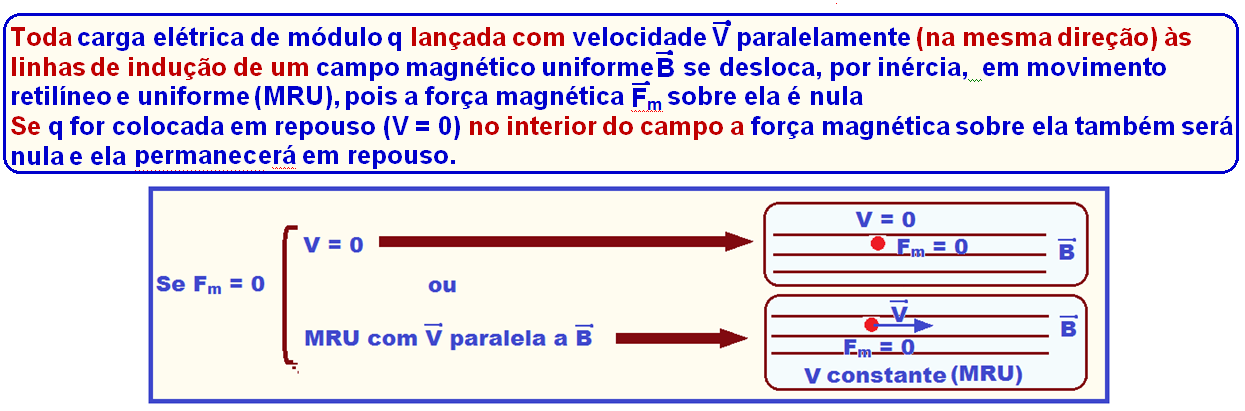
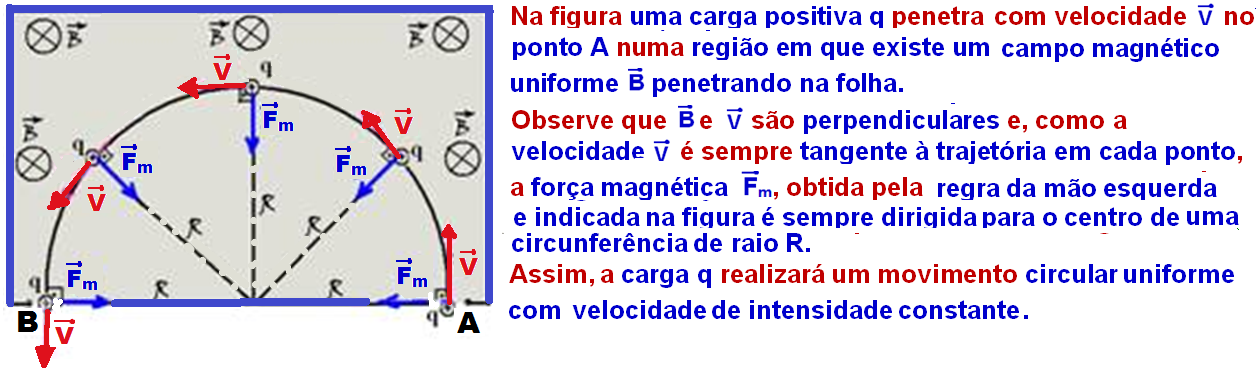
Carga elétrica q lançada com velocidade 
lançada perpendicularmente às linhas de indução de um campo magnético uniforme
Observe que, neste caso o ângulo entre e é 90o (são perpendiculares) e que sen90o = 1.
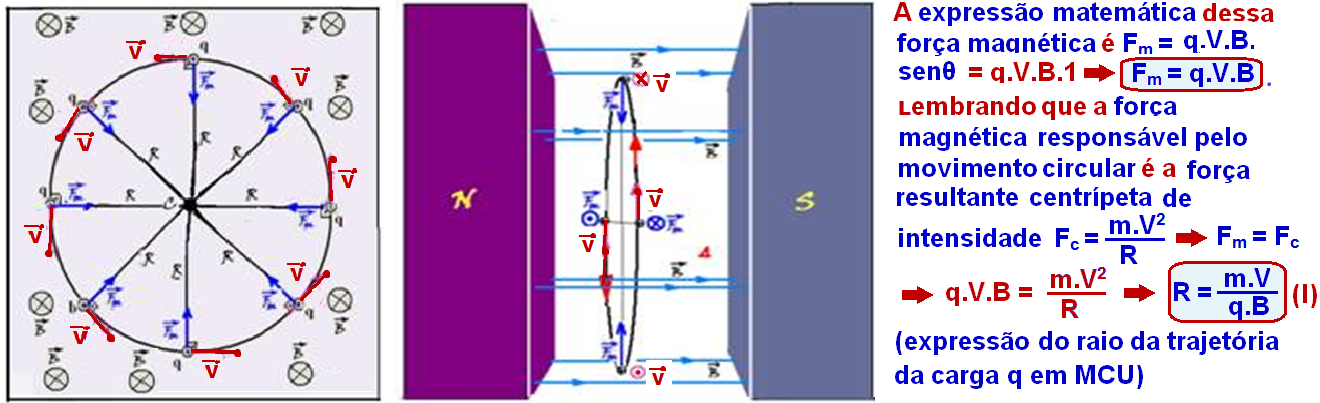
O período T (tempo que a carga q demora para efetuar uma volta completa) é fornecido por 
V = ΔS / Δt numa volta completa ΔS = 2πR e Δt = T V = 2πR / T (II).
Substituindo II em I R = m. (2πR/T)/q.B T = 2πm/q.B (período do MCU).
Observe que o período (T) do movimento circular não depende da velocidade com que a partícula q penetra no campo magnético e nem do raio da circunferência.
O que você deve saber, informações e dicas
Observe na expressão do período (T) que ele não depende da velocidade da partícula, nem do raio da circunferência.
O trabalho realizado por sobre q é nulo, pois é perpendicular ao plano formado por e e W = Fm.d.cos900 = Fm.d.0 = 0.
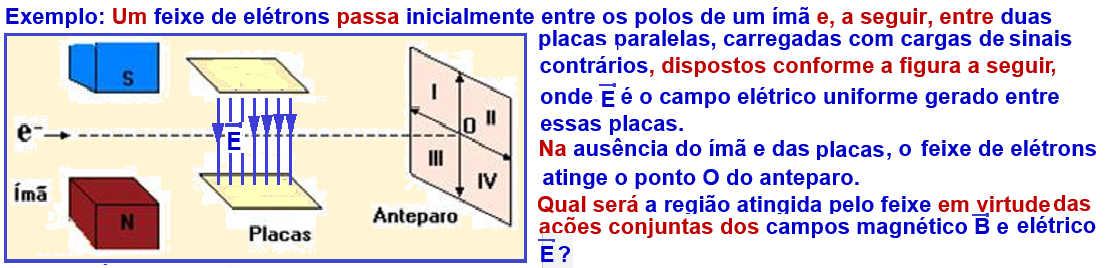
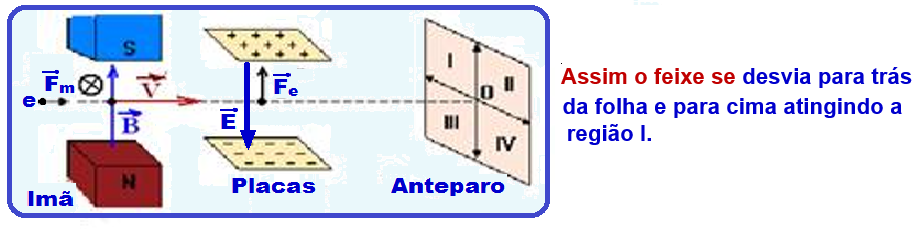
Campos magnético e elétrico agindo sobre uma partícula ou feixe de partículas eletrizadas com carga q
