Aplicações das leis de Newton sem Atrito
Aplicações das leis de Newton sem Atrito
01-(ENEM-MEC)

O ônibus espacial Atlantis foi lançado ao espaço com cinco astronautas a bordo e uma câmera nova, que iria substituir uma outra danificada por um curto-circuito no telescópio Hubble.
Depois de entrarem em órbita a 560 km de altura, os astronautas se aproximaram do Hubble. Dois astronautas saíram da Atlantis e se dirigiram ao telescópio.
Ao abrir a porta de acesso, um deles exclamou: “Esse telescópio tem a massa grande, mas o peso é pequeno.”

Considerando o texto e as leis de Kepler, pode-se afirmar que a frase dita pelo astronauta
a) se justifica porque o tamanho do telescópio determina a sua massa, enquanto seu pequeno peso decorre da falta de ação da aceleração da gravidade.
b) se justifica ao verificar que a inércia do telescópio é grande comparada à dele próprio, e que o peso do telescópio é pequeno porque a atração gravitacional criada por sua massa era pequena.
c) não se justifica, porque a avaliação da massa e do peso de objetos em órbita tem por base as leis de Kepler, que não se aplicam a satélites artificiais.
d) não se justifica, porque a força-peso é a força exercida pela gravidade terrestre, neste caso, sobre o telescópio e é a responsável por manter o próprio telescópio em órbita.
e) não se justifica, pois a ação da força-peso implica a ação de uma força de reação contrária, que não existe naquele ambiente. A massa do telescópio poderia ser avaliada simplesmente pelo seu volume.
![]()
02-(PUC-SP)

Um fio, de massa desprezível, está preso verticalmente por uma de suas extremidades a suporte. 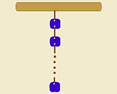
A tração máxima que o fio suporta, sem se romper, é de 5,80N. Penduram-se sucessivamente objetos de 50g cada, separados um do outro de uma distância de 10cm, até o fio se romper. (g=10m/s2).
Quantos objetos foram pendurados e onde o fio se rompeu?
a) 9 objetos; entre o oitavo e o nono objetos.
b) 10 objetos; entre o nono e o décimo objetos.
c) 11 objetos; entre o primeiro e o segundo objetos.
d) 12 objetos; entre o primeiro e o segundo objetos.
e) 12 objetos; entre o suporte e o primeiro objeto.
03-UNIFESP-SP)

Suponha que um comerciante inescrupuloso aumente o valor assinalado pela sua balança, empurrando sorrateiramente o prato para baixo com uma força de módulo F=5,0 N, na direção e sentido indicados na figura.
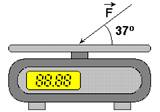
Com essa prática, ele consegue fazer com que uma mercadoria de massa 1,5 kg seja medida por essa balança como se tivesse massa de: considere g=10m/s2 e sen37o = 0,6
![]()
04-(UFSCAR-SP)

O joão-teimoso é um boneco que, deslocado de sua posição de equilíbrio, sempre volta a ficar em pé. Suponha que uma criança segure um joão-teimoso na posição da figura e logo em seguida o solte, sobre uma superfície horizontal. Assinale a alternativa que melhor representa o esquema das forças que, com exceção das forças de atrito, atuam sobre o joão-teimoso deitado, imediatamente após ser solto pela criança.

05-(FUVEST-SP)

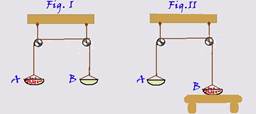
A figura I, a seguir, indica um sistema composto por duas roldanas leves, capazes de girar sem atrito, e um fio inextensível que possui dois suportes em suas extremidades. O suporte A possui um certo número de formigas idênticas, com 20 miligramas cada. O sistema está em equilíbrio. Todas as formigas migram então para o suporte B e o sistema movimenta-se de tal forma que o suporte B se apóia numa mesa, que exerce uma força de 40 milinewtons sobre ele, conforme ilustra a figura II.
Determine o número total de formigas: (considere g=10m/s2).
![]()
06-(UFMT-MT)

A ordem de grandeza de uma força de 1.000N é comparável ao peso de: (considere g=10m/s2)

a) um lutador de boxe
b) um tanque de guerra
c) um navio quebra-gelos
d) uma bola de futebol
e) uma bolinha de pingue-pongue
07-(PUC-MG)

Um astronauta na Lua quer medir a massa e o peso de uma pedra. Para isso ele realiza as seguintes experiências:

I – Para medir a massa, ele utiliza uma balança de braços iguais, colocando em um dos pratos a pedra e, no outro, massas de valor conhecido, até obter o equilíbrio da balança.
II – Para medir o peso, ele utiliza um dinamômetro na vertical, pendurando a pedra na extremidade e lendo seu peso na escala do aparelho.
III – Para medir a massa, ele deixa a pedra cair de uma certa altura e mede o tempo de queda, comparando-o com o tempo de queda de um objeto de massa conhecida, solto da mesma altura; a relação entre os tempos é igual à relação entre as massas.
IV – Para medir o peso da pedra, o astronauta a prende na ponta de um fio que passa por uma roldana fixa vertical; na outra ponta do fio, ele pendura objetos de peso conhecido, um de cada vez, até que consiga o equilíbrio, isto é, até que a roldana pare de girar.
As experiências CORRETAS são:
a) I e II apenas.
b) III e IV apenas.
c) I, II e IV apenas.
d) I, II, III e IV.
08- (UFABC-SP)

Um mecânico afirma ao seu assistente que é possível erguer e manter um carro no alto e em equilíbrio estático, usando-se um contrapeso mais leve do que o carro. A figura mostra, fora de escala, o esquema sugerido pelo mecânico para obter o seu intento.
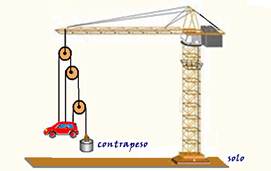
Considerando as polias e os cabos como ideais e, ainda, os cabos convenientemente presos ao carro para que não haja movimento de rotação, a massa mínima do contrapeso e o valor da força que o cabo central exerce sobre o carro, com massa de 700 kg, quando esse se encontra suspenso e em equilíbrio estático são, respectivamente:.
Dado: Adote g = 10 m/s2
a) 100kg e 2.000N
b) 200kg e 2.000N
c) 500kg e 1.000N
d) 500kg e 1500N
e) 150kg e 1000N
09- (UNIFESP-SP)

Às vezes, as pessoas que estão num elevador em movimento sentem uma sensação de

desconforto, em geral na região do estômago. Isso se deve à inércia de nossos órgãos internos localizados nessa região, e pode ocorrer:
a) quando o elevador sobe ou desce em movimento uniforme.
b) apenas quando o elevador sobe em movimento uniforme
c) apenas quando o elevador desce em movimento uniforme.
d) quando o elevador sobe ou desce em movimento variado.
e) apenas quando o elevador sobe em movimento variado.
10-(ITA-SP)

Uma pilha de seis blocos iguais, de mesma massa m, repousa sobre o piso de um elevador, como mostra a figura.
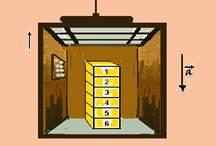
O elevador está subindo em movimento uniformemente retardado com aceleração de módulo a. O módulo da força que o bloco 3 exerce sobre o bloco 2 é dado por:
a) 3m(g + a)
b) 3m(g – a)
c) 2m(g + a)
d) 2m(g – a)
e) m(2g – a)
11-(UFRJ-RJ)

Um sistema é constituído por um barco de 100 kg, uma pessoa de 58 kg e um pacote de 2,0 kg que ela carrega consigo. O barco é puxado por uma corda de modo que a força resultante sobre o

sistema seja constante, horizontal e de módulo 240 newtons. Supondo que não haja movimento relativo entre as partes do sistema, o módulo da força horizontal que a pessoa exerce sobre o pacote vale em newtons:
![]()
12-(MACKENZIE-SP)

O sistema abaixo é constituído por fios e polias ideais, num local onde g=10m/s2.
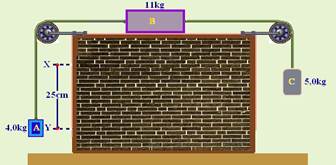
Desprezando-se qualquer tipo de resistência e abandonando-se o conjunto quando o corpo A se encontra na posição X, a sua velocidade, ao passar por Y, é, em m/s:
![]()
13-(UNESP-SP)

Em uma circular técnica da Embrapa, depois da figura, encontramos uma recomendação que, em resumo, diz:

“No caso do arraste com a carga junto ao solo (se por algum motivo não pode ou não deve e ser erguida . . .) o ideal é arrastá-la. . . reduzindo a força necessária para movimentá-la, causando menos dano ao solo . . . e facilitando as manobras. Mas neste caso o peso da tora aumenta. (www.cpafac.embrapa.br/pdficirtec39.pdf.Modificado.)
Pode-se afirmar que a frase destacada é conceitualmente
a) inadequada, pois o peso da tora diminui, já que se distribui sobre uma área maior.
b) inadequada, pois o peso da tora é sempre o mesmo, mas é correto afirmar que em II a força exercida pela tora sobre o solo aumenta;
c) inadequada: o peso da tora é sempre o mesmo e, além disso, a força a força exercida pela tora sobre o solo em II diminui, pois se distribui por uma área maior.
d) adequada, pois nessa situação a tora está integralmente apoiada sobre o solo.
d) adequada, pois nessa situação a área sobre a qual a tora está apoiada sobre o solo também aumenta.
14-(UFRN-RN)

É muito comum observarmos nas fachadas de edifícios em construção andaimes constituídos por uma tábua horizontal sustentada por cordas que passam por roldanas presas no topo da edificação. O fato de um dos operários se deslocar sobre o andaime em direção ao outro, por exemplo, quando vai entregar alguma ferramenta ao companheiro, afeta a distribuição de forças sobre as cordas. Nesse sentido, considere a situação mostrada na Figura abaixo. Nela, um dos operários se encontra

na extremidade esquerda do andaime, enquanto o outro, após ter caminhado em direção a ele, conduzindo uma marreta, encontra-se parado no meio do andaime.
Considerando a situação mostrada na Figura, pode-se afirmar que a
A) força resultante sobre o andaime é diferente de zero e a tensão na corda Y é maior que na corda X.
B) força resultante sobre o andaime é igual a zero e a tensão na corda Y é maior que na corda X.
C) força resultante sobre o andaime é diferente de zero e a tensão na corda X é maior que na corda Y.
D) força resultante sobre o andaime é igual a zero e a tensão na corda X é maior que na corda
15-(UFPR-PR)

O empregado de uma transportadora precisa descarregar de dentro do seu caminhão um balcão de 200 kg. Para facilitar a tarefa do empregado, esse tipo de caminhão é dotado de uma rampa, pela qual podem-se deslizar os objetos de dentro do caminhão até o solo sem muito esforço.
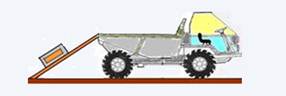
Considere que o balcão está completamente sobre a rampa e deslizando para baixo. O empregado aplica nele uma força paralela à superfície da rampa, segurando-o, de modo que o balcão desça até o solo com velocidade constante. Desprezando a força de atrito entre o balcão e a rampa, e supondo que esta forme um ângulo de 30° com o solo, determine o módulo da força paralela ao plano inclinado exercida pelo empregado (g=10m/s2).
![]()
16- (UFB) A mola helicoidal (figura 1), de constante elástica k = 12 N/m foi partida em 3 partes iguais.
Em seguida essas três partes foram associadas em paralelo (figura 2) e em série (figura 3).
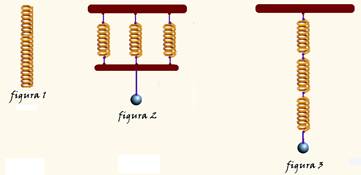
As massas das figuras 2 e 3 são iguais e valem 100g. Adote g=10m/s2 e determine:
a) a constante elástica de cada parte.
b) o período de oscilação do conjunto quando as três molas estão associadas em paralelo.
c) o período de oscilação do conjunto quando as três molas estão associadas em série.
Confira a resolução comentada