Blindagem eletrostática – Condutor em equilíbrio eletrostático
Condutor em equilíbrio eletrostático – Blindagem eletrostática
Condutor em equilíbrio eletrostático
Características de um condutor em equilíbrio eletrostático
No interior do condutor em equilíbrio eletrostático, onde não existem cargas em excesso, o campo elétrico 
deve ser nulo e o potencial elétrico V constante, caso contrário haveria movimento ordenado de elétrons, pois eles só se movem se houver diferença de potencial.
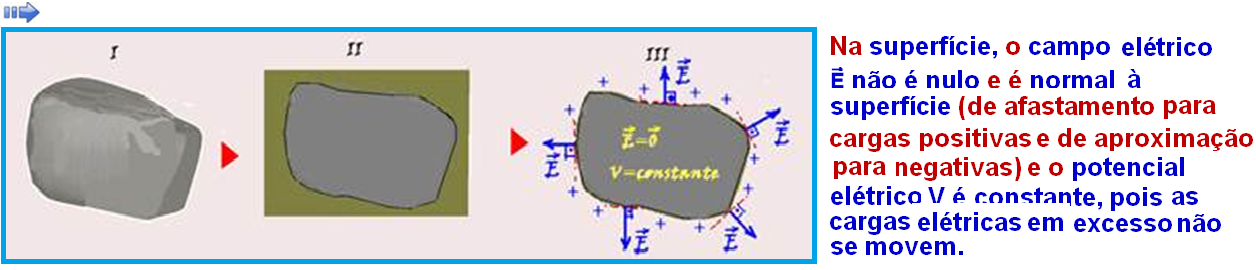
Em todo condutor em equilíbrio eletrostático, oco ou maciço, a densidade, ou seja, a concentração de cargas elétricas é maior nas regiões mais pontiagudas. Por isso, nessas regiões a intensidade do campo elétrico 
é maior e, se o condutor estiver eletrizado com cargas
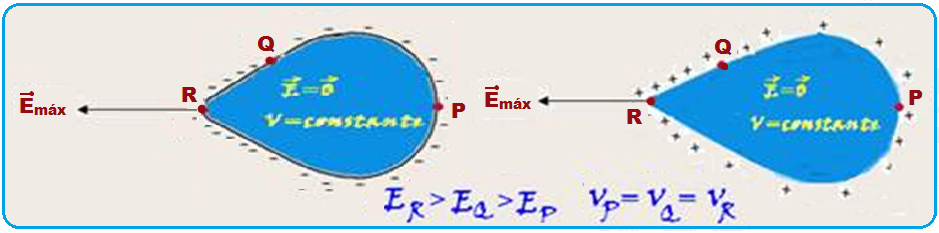
negativas é até possível que possa ocorrer emissões de elétrons em suas pontas.
Blindagem eletrostática 
se, no interior de um condutor oco em equilíbrio eletrostático o campo elétrico é nulo, qualquer aparelho elétrico e eletrônico, quando colocado em seu interior ficará protegido de influências perturbadoras externas.
Esse fenômeno foi comprovado experimentalmente por Michael Faraday ao encerrar-se no interior de uma gaiola condutora, onde verificou não haver manifestação de fenômenos elétricos no seu interior. Essa gaiola deve ser feita de material condutor de eletricidade e não precisa ser contínua, podendo ser uma rede metálica, por isso recebeu o nome de gaiola.
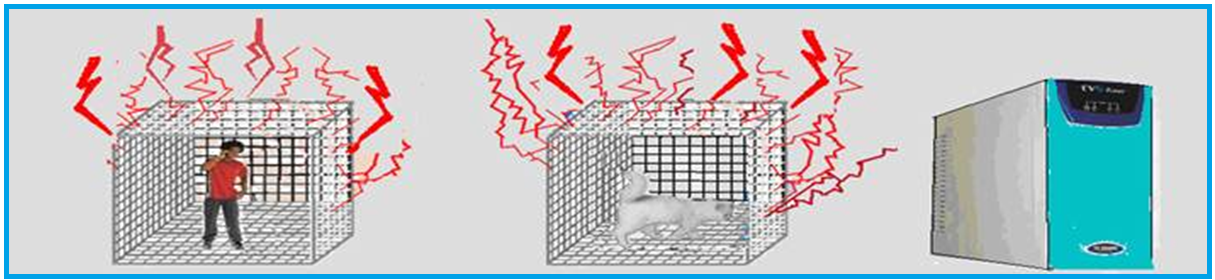Foi adaptada para proteger instrumentos e aparelhos de grande sensibilidade colocados em seu interior.
A blindagem eletrostática (gaiola de Faraday) também é utilizada nos carros e aviões, oferecendo proteção contra descargas
elétricas. Construções também são feitas utilizando blindagem eletrostática, a fim de proteger seus equipamentos elétricos e eletrônicos.
Se uma gaiola de Faraday fosse constituída por uma malha metálica, onde os “buracos” tivessem dimensões menores de 15 cm, não haveria a penetração de campos elétricos em seu interior, tornando-a blindada às ondas eletromagnéticas na faixa da telefonia móvel (da ordem de 1.800MHz).
No entanto, isso não é feito pelo alto custo, preferindo-se a utilização da interferência, emitindo-se ondas nessa faixa de freqüência com intensidade muito maior.
Campo e potencial elétrico de um condutor esférico
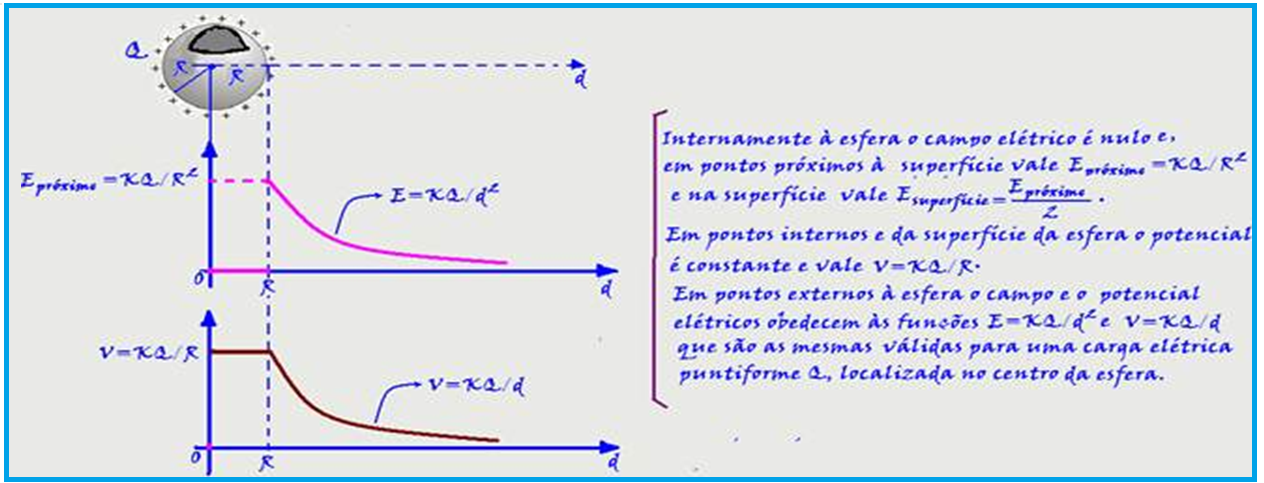
O que você deve saber, informações e dicas
Equilíbrio eletrostático entre dois condutores 
sejam dois condutores esféricos A e B, de raios RA e RB respectivamente, com cargas elétricas QA e QB epotenciais elétricos diferentes VA e VB (fig. I).
Unindo-os por um fio condutor ou encostando-os haverá passagem de cargas elétricas entre eles até que seja atingido o equilíbrio eletrostático quando atingem o mesmo potencial V (figura III).
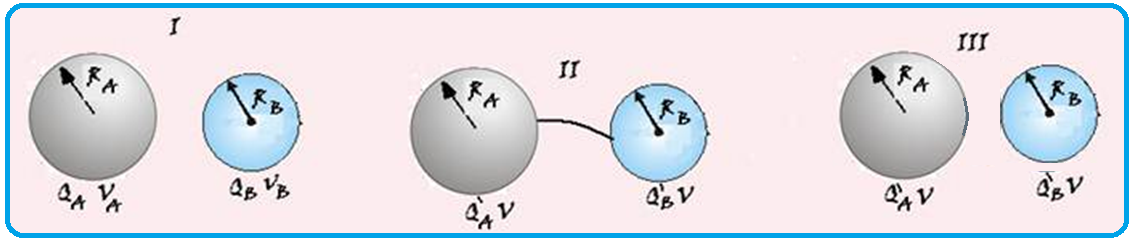
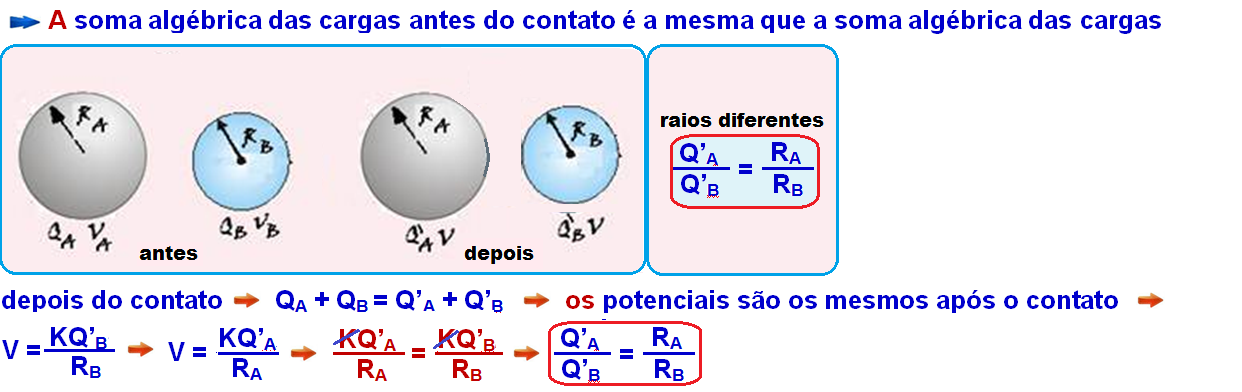
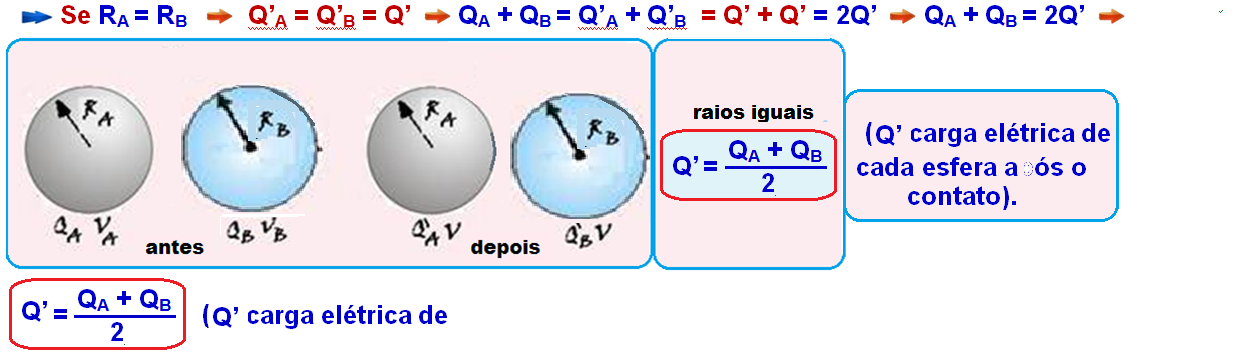
Sejam Q’A e Q’B as novas cargas após o contato. Têm-se duas condições:
No interior do condutor em equilíbrio eletrostático, onde não existem cargas em excesso, o campo elétrico deve ser nulo e o potencial elétrico V constante, caso contrário haveria movimento ordenado de elétrons, pois eles só se movem se houver diferença de potencial.
Em todo condutor em equilíbrio eletrostático, oco ou maciço, a densidade, ou seja, a concentração de cargas elétricas é maior nas regiões mais pontiagudas.Por isso, nessas regiões a intensidade do campo elétrico é maior e, se o condutor estiver eletrizado com cargas
negativas é até possível que possa ocorrer emissões de elétrons em suas pontas.
Blindagem eletrostática Como, no interior de um condutor oco em equilíbrio eletrostático o campo elétrico é nulo, qualquer aparelho elétrico e eletrônico, quando colocado em seu interior ficará protegido de influências perturbadoras externas.
Campo e potencial elétrico de um condutor esférico:
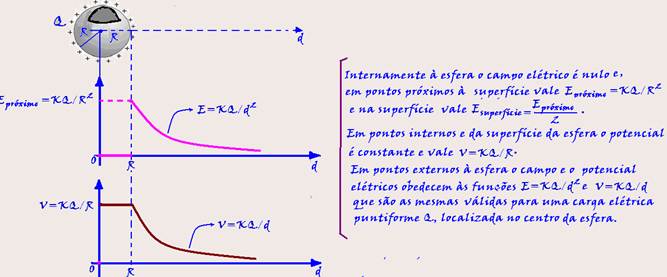
Densidade elétrica superficial Você já sabe que em corpos condutores eletrizados as cargas elétrica em excesso, que se repelem, localizam-se o mais longe possível, ou seja, na superfície externa. Assim, quanto maior a carga elétrica, maior sua concentração superficial.
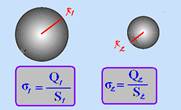
A densidade elétrica superficial (σ) mede a concentração de carga elétrica (Q) pela superfície (área S) σ=Q/S no caso de esfera de raio R, a área da superfície esférica é fornecida por S = 4πR2.