Circuitos Compostos

 

Características dos elementos de um circuito elétrico

 Considere o circuito elétrico esquematizado na figura abaixo onde, A₁, A₂, A_{3, .} . . . . . . ., A₁₂ são

bipolos.

Definições dos principais elementos de um circuito elétrico

  nó da rede ponto de interligação de pelo menos dois condutores. São nós os pontos A, B e C.

 ramo da rede trecho da rede compreendido entre dois nós consecutivos. São ramos os trechos: BFDA, AEC e BGHC, AB e BC.

 malha da rede toda cadeia de ramos que forma um circuito fechado. Assim, todo circuito poligonal fechado constitui uma malha. São malhas: ABFDA, AECBA e BGHCB.

 Primeira lei de Kirchhoff ou lei dos nós: “A soma algébrica das correntes que chegam a um nó é igual à soma algébrica das correntes que saem do mesmo nó”.

Exemplo numérico    determine a intensidade da corrente i₃ do trecho de circuito abaixo:

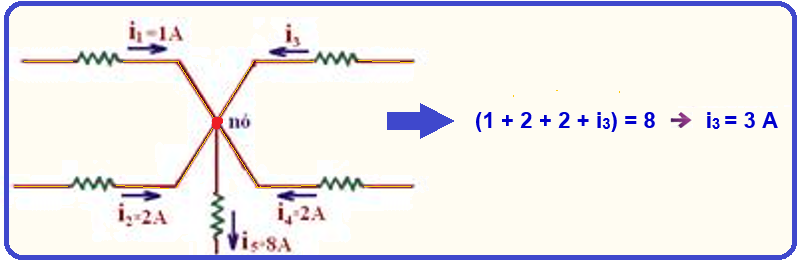
Segunda lei de Kirchhoff ou lei das malhas: “Percorrendo uma malha num mesmo sentido, é nula a soma algébrica das tensões encontradas em cada elemento do circuito”

Baseado na lei acima, escolhendo um sentido de percurso para cada malha, partindo de um ponto, retornando ao mesmo ponto e igualando esta soma algébrica de tensões a zero, você pode estabelecer as seguintes convenções:

 Convenção para o sinal de E:

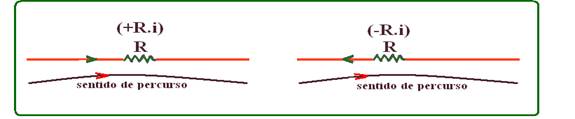
 Convenção para o sinal de R.i

Quando o sentido da corrente i coincidir com o sentido do percurso escolhido para a malha, o sinal de R.i será positivo e quando o sentido da corrente i não coincidir com o sentido de percurso escolhido para a malha, o sinal R.i será negativo.

 

Sequência de operações para resolução de exercícios sobre circuitos compostos

1^a  Assinalar com letras maiúsculas os nós da rede.

2^a  Atribuir a cada ramo uma corrente com sentido arbitrário.

3^a  Atribuir polaridade arbitrária a eventuais bipolos que não as tenham.

4^a  Aplicar a primeira lei de Kirchhoff a cada nó.

5^a  Atribuir a cada malha independente um sentido arbitrário (horário ou anti-horário) de percurso.

6^a  Aplicar a segunda lei de Kirchhoff, ou seja, percorrer cada malha obedecendo ao percurso fixado e às convenções vistas anteriormente.

7^a  Resolver o sistema de equações obtidas em 4^a e 6^a.

8^a  Interpretar os resultados, lembrando que:

a) deve-se inverter o sentido das correntes que resultarem negativas.

b) Inverter as polaridades das tensões que resultarem negativas.

9^a  Para fornecer as respostas deve-se, depois de corrigir no esquema os sentidos das correntes e das polaridades das tensões, expressa-las por números positivos.

Deve-se observar, no cálculo da diferença de potencial entre dois pontos quaisquer de um circuito, que, se quiser determinar a ddp (U_AB=V_A – V_B) entre dois pontos A e B, deve-se seguir o circuito de A até B obtendo determinado valor em volt e que, se seguir em sentido contrário obterá resultado simétrico.

Deve-se lembrar que, num gerador, o sentido da corrente é do polo negativo para o polo positivo, ao contrário do receptor. 

Exemplos de exercícios sobre a aplicação da sequência acima, ou seja, como proceder para resolver exercícios sobre circuitos compostos:

 Dado o ramo do circuito abaixo, determine a diferença de potencial entre os pontos A e D, sabendo que a corrente flui de A para D e tem intensidade de 3 A.

Percorrendo o ramo no sentido de A para D e observando as convenções de sinais para E e para R.i (veja informações acima)    U_AD = V_A – V_D = +(2.3) – 6 +(3.3) + 2 +(2.3)  + 2 +(4.3)    U_AD = V_A – V_D= +31V    se você tivesse percorrido o ramo de D para A, obedecendo as mesmas convenções, você teria obtido U_DA = V_D – V_A = – 31V

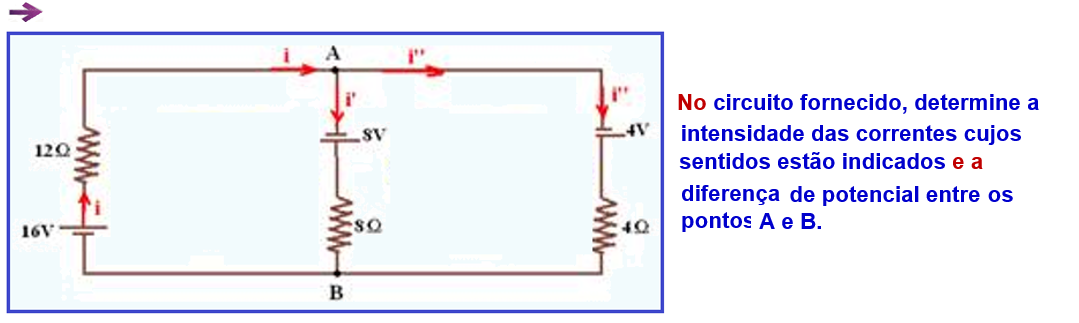
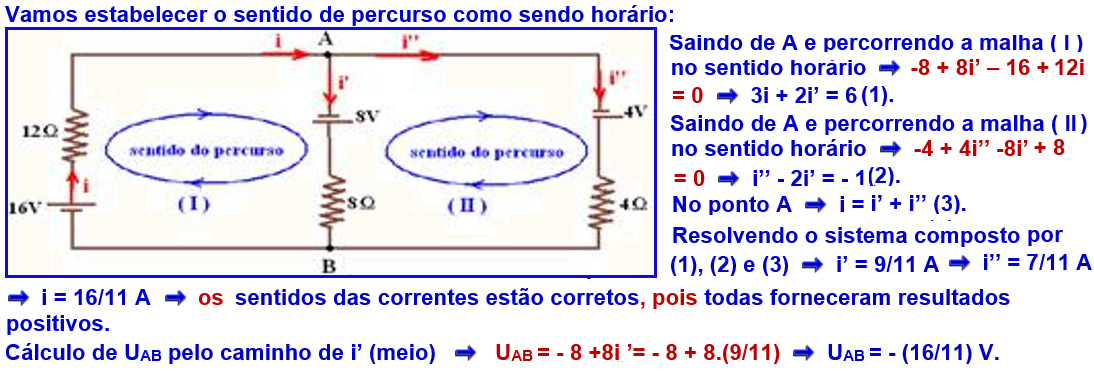
 No circuito esquematizado, determine a intensidade e o sentido da corrente elétrica e a diferença

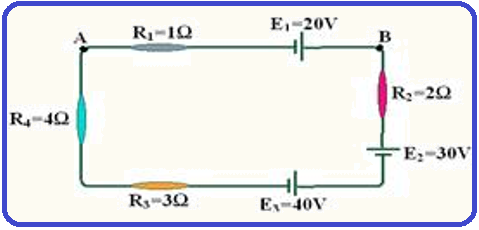
de potencial entre A e B. Estabeleça para a corrente e para o percurso o sentido horário.

Esse assunto é trabalhoso e é importante que você resolva no mínimo alguns exercícios, analisando atentamente as resoluções. Selecionei alguns que são os de números 03, 06, 11, 16, 20 e 22.

 

Confira os exercícios sugeridos